Algebra II Fall Semester Final Review Dec. 2011 Name ______

Unit 1

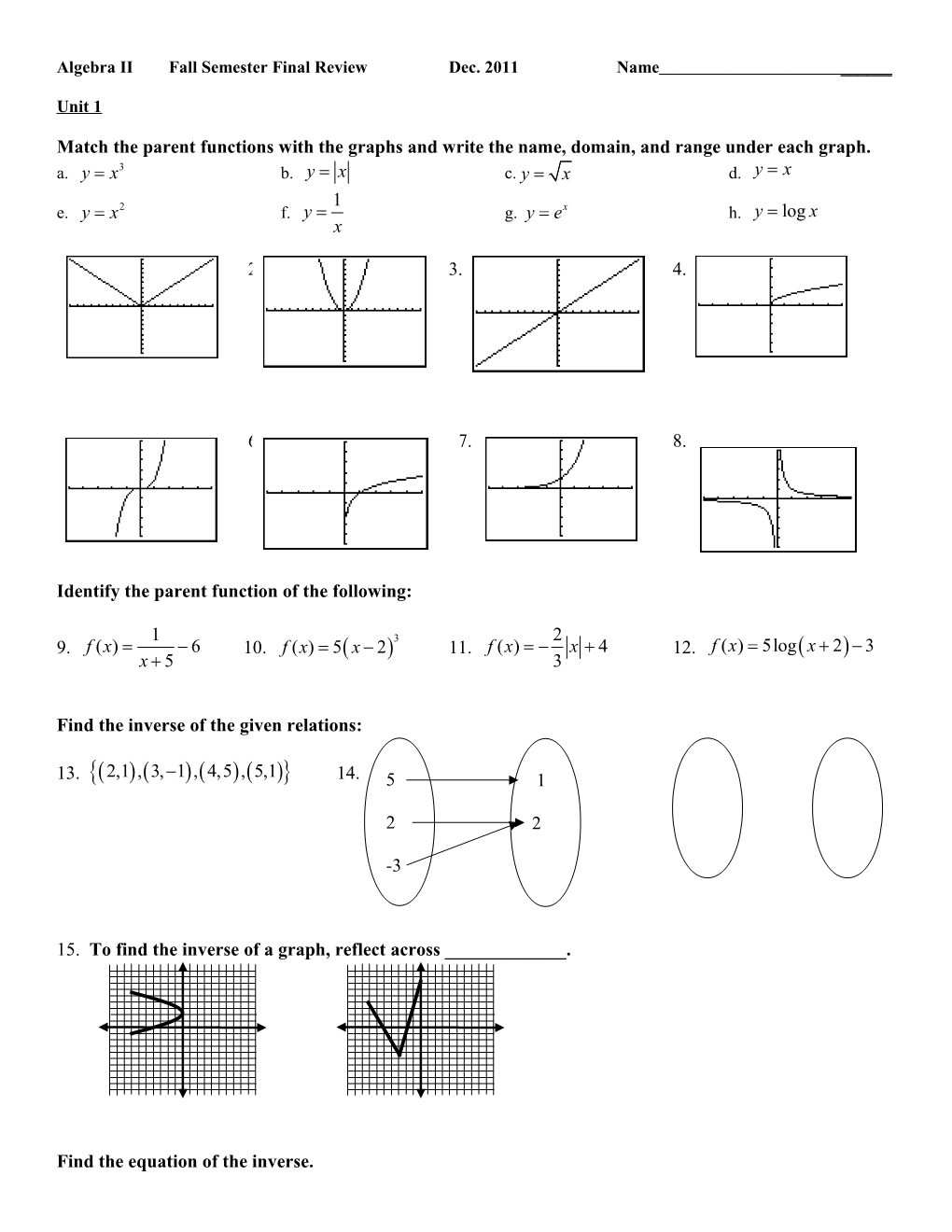
Match the parent functions with the graphs and write the name, domain, and range under each graph. a. y= x3 b. y= x c. y= x d. y= x 1 e. y= x2 f. y = g. y= ex h. y= log x x

1. 2. 3. 4.

5. 6. 7. 8.

Identify the parent function of the following:

1 3 2 9. f( x )= - 6 10. f( x )= 5( x - 2) 11. f( x )= - x + 4 12. f( x )= 5log( x + 2) - 3 x + 5 3

Find the inverse of the given relations:

13. {(2,1) ,( 3,- 1) ,( 4,5) ,( 5,1)} 14. 5 1

15. To find the inverse of a graph, reflect across ______.

Find the equation of the inverse. 4 5 16. y= -4 x + 1 17. y=2 x2 + 3 18. y = 19. y= x -1 x - 5 4

Unit 2 y = a (x - h) + k

How does each transform the graph? a - ______, h - ______, k - ______

Identify the parent function and describe the transformations: 1 1 1. f( x )= + 3 2. f( x ) = - x2 3. f( x )= - x + 3 - 7 x 2

1 4. f( x )= - 4 x + 8 5. f( x )= ( x - 7)2 - 2 6. f( x )= 3 x3 - 2 2

Unit 3 – Curve Fitting 1 – 3: Use the data provided in the table to answer each question. x - 1 0 1 2 3 y 10 8 6 4 2

1) What is the slope of the linear function? 2) What will the value of y be when x is 10?

3) Write the equation that represents the equation of best fit. 4) What is the correlation coefficient?

5 – 7: Use the data provided in the table to answer each question. x - 1 0 1 2 3 y - 6 - 5 - 2 3 10

5) Use finite difference to determine the type of polynomial function 6) Write the equation of best fit.

7) What would be the value of y when x = 8? The table provided shows personal income of Americans from 1998 – 2003. Let x = 0 represent the year 1990. Year Amount (trillions of dollars) 1998 7.4 1999 7.8 2000 8.4 2001 8.7 2002 8.9 2003 9.2 (Source: U.S. Census Bureau. Statistical Abstract of the United States. 2004 -2005)

8) Assume the data is represented by a linear function. Write the equation of best fit.

9) Find the correlation coefficient.

Unit 4a – Writing & Graphing Systems Write the system of equations. Don’t solve!

1. Your teacher gives you a test worth 100 points with 34 questions. Each question is worth either 2 points or 4 points. Write a system of equations to determine the number of 2 point and 4 point questions on the test.

2. Tom bought 12 student tickets and 4 adult tickets to the football game for $56. Renee bought 4 student tickets and 8 adult tickets for $52. Write the system of equations that will determine the cost of adult tickets and the student tickets that they bought.

Use graphing to solve each system of equations.

1. 3x - 4y = 20 y - 2x = 0

Rules for graphing inequalities: < > ≤ ≥

Shade:

2. Graph the system of inequalities.

y�3 x 5 1 y< - x + 4 2

3. Which inequality best describes the graph shown below? 3 A y > − x + 5 4 4 B y < − x + 5 3 3 C y < − x + 5 4 4 D y > − x + 5 3

2003 Exit 4. Which graph best represents all the pairs of numbers (x, y) such that x + y < −6? F G H J

Unit 4b – Solving Systems by Substitution & Elimination

1. Explain what the following terms mean: A. Independent system B. Inconsistent system C. Dependent system

Solve by substitution: y= 6 x -3x - y = - 1 2. 3. x+ y = 28 2x+ 3 y = 24

Solve by the elimination method. 3x+ 2 y = 7 -3x + 5 y = 45 4. 5. 5x- 2 y = 1 3x+ 13 y = 9

6. In the system of equations 4x + 2y = 10 and 3x + 7y = -18, which expression can be correctly substituted for y in the equation 3x + 7y =-18? (A) 10 – 2x (B) 10 + 2x (C) 5 – 2x (D) 5 + 2x

7. Use substitution or elimination to solve these equations. Show your work 6x + y = -2 6x + 2y = 2 8. Use substitution to determine if the given ordered pair is a solution for the system of equations. 轾y= -2 x (-4,8) 犏臌3x+ y = - 4

9. Juan bought 40 drinks, all either cola or root beer. The cola was equal to four times the number of cans of root beer. Write a system of equations to determine the number of cans of cola and root beer he bought. Then solve using the best method.

10. At a restaurant the cost for a breakfast taco and a small glass of milk is $2.10. The cost for 2 tacos and 3 small glasses of milk is $5.15. Write a system to determine t, the cost of a taco, and m, the cost of a small glass of milk. Then solve.

11. The price, e, of an entertainment system at Extreme Electronics is $220 less than twice the price, u, of the same system at Ultra Electronics. The difference in price between the system at Extreme Electronics and Ultra Electronics is $175. Which system of linear equations can be used to determine the price of the system at each store? (A) 2e – u = 220 (B) 2e – u = 220 (C) 2e – 2u = 440 (D) e – 2u = -220 e – u = -175 e + u = 175 e – u = -175 e – u = 175

12. Solve the system you chose from #11 with your best method. Write your solution as an ordered pair.

Unit 5 – Intro to Quadratics

To find axis of symmetry: To find vertex:

Find the axis of symmetry and vertex of the following. Show your work!!!

1. 2x2 – 4x + 5 2. x2 + 6x – 7

Find the roots/x-intercepts/zeros/solutions when y=0 from the graphs and tables below. (Write answer in ordered pair(s).)

3. 4. x y -3 1 -2 0 -1 1 0 4 -1 9 -2 16 Find the following information for the given equation. 5. y = ¾ (x + 2)2 - 3

Opens:

Vertex:

X-intercepts: 6. A ball is tossed straight up at a velocity of 64 ft/sec. The path of the ball is straight up and down. The height of the ball above the ground is modeled by the function h(x) = - 16 x 2 + 64 x. (Use your calculator to graph the path of the ball. Identify what you see a. Line of Symmetry: ______b. Coordinates of the vertex:______c. Roots or Solutions:______d. y-intercept:______

e. What are the coordinates for the maximum height of the ball? Write as an ordered pair

f. What is the height of the ball at 3 seconds?______

g. Write the coordinates that represent the ball reaching the ground. ______

h. Explain what the x values represent in real life. ______

i. Explain what the y values represent in real life. ______

Unit 6– Factoring

Factor the following completely. Remember all types: split the middle, difference of squares, sum and difference of cubes, and grouping.

1. x2 – 5x + 6 2. x2 + 8x + 15 3. x2 – 25 4. x3 – 8

5. 64x3 + 125 **6. 3xy + 15 – 4y – 20 7. 16x2 – 4 8. x2 + 9x + 20

9. 4x2 – 35x + 49 10. 8x2 + 10x – 3 11. 5x2 + 19x + 12 12. x2 – 7x – 30

Complete the square of the following:

13. x2 – 6x + ______= 16 + ______14. x2 + 16x + ______= -39 + ______Unit 7 – Solving Quadratic Equations

Find the solutions to the following quadratic functions.

1. x2 – 1 = 0 2. x2 + 9x +14 = 0 3. x2 + 14x + 49 = 0

4. 5x2 + 7x + 2 = 0 5. 9x2 – 6x + 1 = 0 6. 4x – 12 = 0

Find the equation given the roots/zeros/x-intercepts:

7. x = -3, x = 5 8. x = -1/4, x = 2 9. x = 1/3, x = -7

For each question, identify the type and number of roots using the discriminant and then solve to find the roots.

10) -x2 - 5x + 6 11) 8x2 + 10x – 3 # roots: # roots: Type: Type: Solution: Solution:

12) 3x2 − 4x – 1 # roots: Type: Solution:

Solve the following by completing the square. 13. x2 – 2x – 8 = 0 14. 2x2 + 16x = 18 15. x2 – 10x = 10 Unit 8 – Real World Applications of Quadratics

1 – 3 A ball is tossed straight up at a velocity of 64 ft/sec. The path of the ball is straight up and down. The height of the ball above the ground is modeled by the function h(t) = -16t2 + 64t. (Use your calculator to graph the path of the ball. Identify what you see on your calculator screen by finding the following. You can also use your table.)

1. What is the maximum height of the ball?______

2. How long does it take for the ball to reach its maximum height?______

3. How long until the ball lands?______

Unit 9 – Quadratic Forms

1) Describe the transformation of the given quadratic as compared to y = x2: y = -2(x + 1)2 – 4

2) Place the functions in order from the widest to the narrowest. y = 2x2 y = x2 y = -5x2 y = 0.3x2

3) Graph y = -(x + 2)(x – 3) 4) Convert y = -5(x + 2)(x – 1) into standard form.

5) Convert y = x2 – 5x – 6 into factored form. 6) Convert y = x2 + 8x – 10 into vertex form.

7) Find the length of the base and height of a triangle if the base is 2x + 4 and the height is x – 6 having an area of 48 u2.