Percent Means an Amount Or Quantity out of 100

Percent

Percent means an amount or quantity out of 100

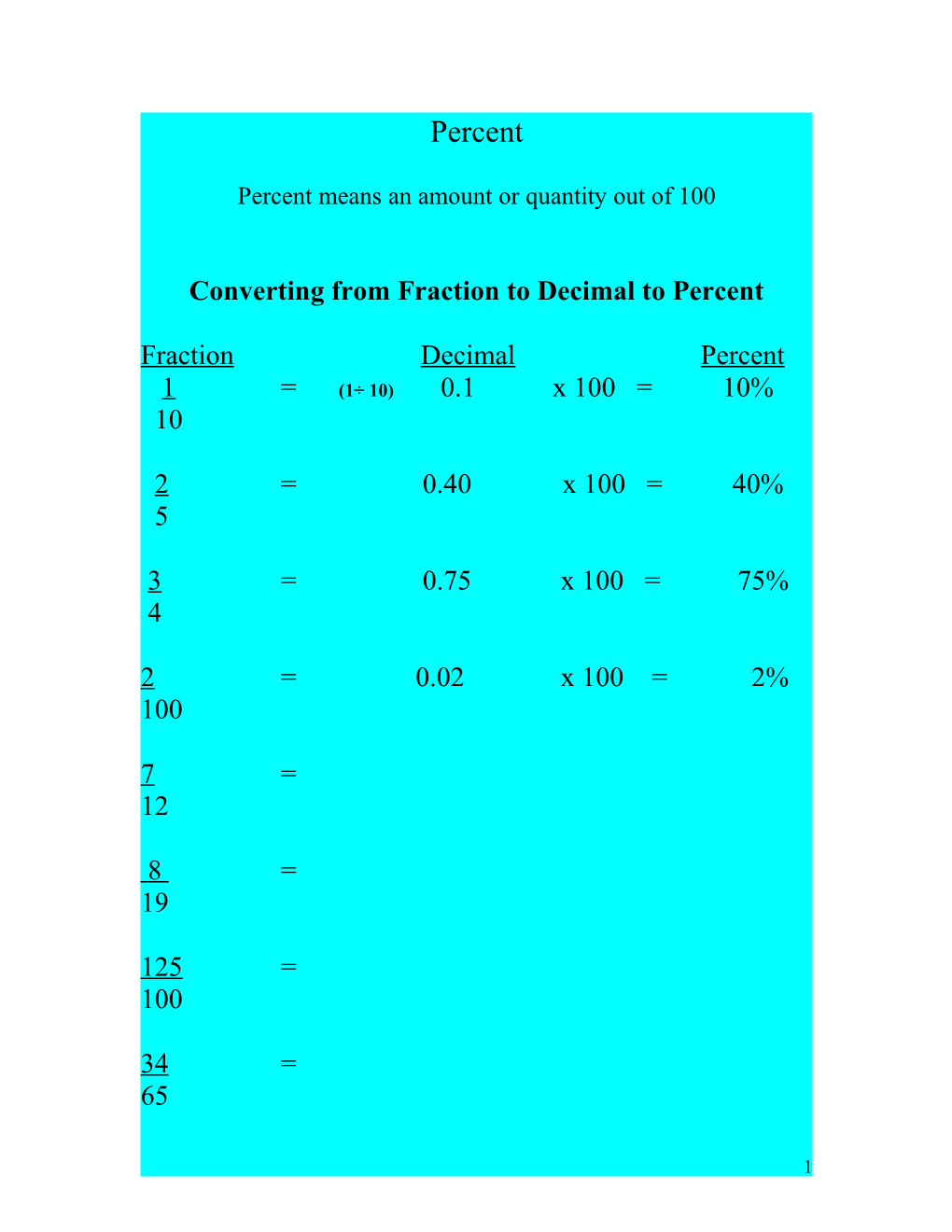
Converting from Fraction to Decimal to Percent

Fraction Decimal Percent 1 = (1÷ 10) 0.1 x 100 = 10% 10

2 = 0.40 x 100 = 40% 5

3 = 0.75 x 100 = 75% 4

2 = 0.02 x 100 = 2% 100

7 = 12

8 = 19

125 = 100

34 = 65

1 Converting from Percent to Fraction to Decimal

Percent Fraction Decimal

26% = (26% ÷ 100) 26 = 0.26 100

83% = 83 = 0.83 100

146% = 146 = 1.46 100

2 Converting from Percent to Decimal to Fraction

Percent Decimal Fraction

65% (65% ÷ 100) 0.65 65 100

3 Examples of Percents of an Amount or Quantity

A) Percents greater than 1% but less than 100%:

20% of $36.00 = 20 or .20 x $36 = $7.20 100

B) Percents greater than 100%:

130% of $36.00 = 130 or 1.30 x $36 = $46.80 100

C) Percents less than 1% (fractional percents):

3 % of $36.00 = 0.75% of $36. = 0 .75 = 0.0075 x $36.00 = $0.27 4 100

4 Fractional Percents and Percents Greater than 100%

0 1% 50% 100%

Fractional Percents are greater than 0 but less than 1%

Understand: 1 % does not equal the fraction 1 or 0.5 2 2

1% = 0.5% = 0 .5 = 0.005 (five thousandths not five tenths) 2 100

Jane said she believed 2/3% per year of Interest on her bank account was a good rate of Interest. Do you agree? Why or why not?

Together do 1 2 3 4

From your handout “Working with Mathematics” do 2abcghi, 3adgh, 4adeghlm, 5abcil, 6aeimno, 7aegjm, 8agjkop

5 Solving Percent Problems

What is 3 % of $30.00? 7

A) You can convert 3/7% to 0.43% and then use the percent keying sequence on your calculator

B) You can convert 3/7% to 0.43% then to decimal 0.0043 and then multiply 0.0043 x $30 with your calculator

C) You can use the Percent formula which is the same as the Proportion formula:

Proportion formula: x = 23 6 41

Percent Formula: % = Part (is) 100 Whole (of)

Understand: the “larger” quantity is not necessarily the “Whole” ex. What percent is $15 of $6? x % = $15 100% $ 6

6 The Percent Formula solves most percent problems x % = Part (is) 100% Whole (of)

Let’s use a shortcut!

A) Find the part of a number: What is 28% of $1200.00?

B) Find the percent one number is of another number:

What percent of $15 is $12?

C) Find the whole when the part and percent are given:

25% of what number is $48?

Let’s solve other percent problems using this formula

7 Definitions and Formulas

Cost Price is what the store pays for a product

Markup is the amount added to the store’s Cost Price. It is the store’s profit on the item

Markup Rate is the Mark Up in percent form

Mark Up Rate% = Mark Up $ 100% Cost Price

Selling Price (Retail Price or Regular Price) = Cost Price + Mark Up $ Mark Up = Selling Price - Cost Price

Discount (amount subtracted from the store’s Selling Price). The Discount is how much the store’s profit is reduced by.

Discount Rate is the Discount in percent form

Discount Rate% = Discount $ 100% Selling Price

Sale Price = Selling Price - Discount $

8 Commission is the amount of money a salesperson receives from the store when he or she sells an item. Commission is a percentage of the item’s Selling Price or Sale Price.

Commission Rate% = Commission $ 100% Selling Price

Other Percent Formulas

Percent Increase = amt. of increase x 100 = % original

Percent Decrease = amt. of decrease x 100 = % original

Markup Rate = amt. of increase x 100 = % Cost Price

Discount Rate = amt. of decrease x 100 = % Selling Price

9 Textbook

from CD do 1(13%) 2adgh

6ab 7ab (together) 8a 9a 10a

Problems

1. The markup rate is 30% on a calculator. The store paid $21.25 for the calculator. What is the Selling Price?

2. The store buys a pair of socks for $11 and sells it for $16. What is the markup rate?

3. The Selling Price for a shirt is $79. The discount rate is 15%. What is the amount of discount? What is the Sale Price?

4. Mr. Brown sold the sports car on display for $26 950. His commission rate is 2.5%. How much money did he earn?

10 5. A store was selling a Blue Ray Disc for $69. The manager decided to drop the price to $39.99. What is the percent decrease?

6. Calculate the retail price of a pair of jeans where the store’s cost is $44.25 and the markup rate is 15%.

7. In a survey of 270 Grade 9 students, 58% liked Rap music. How many students did not like Rap music?

8. Mrs. Green bought a dot.com stock at $35 a share. Two weeks later, she sold it for $108. What is the percent increase?

9. Mary’s soccer team won 12 games and lost 8 games. What percent of the 20 games did her team win?

10. In Miss Young’s class, 9 students have black hair. This is 25% of the class. How many students are in her class?

11. A store is marking up “PSP portable” by 150%. If each cost the store $129.15, what is the selling price for each?