Highway Design for Performance

CE 361 Introduction to Transportation Engineering Posted: Thurs. 7 September 2006 Homework 3 (HW 3) Solutions Due: Mon. 18 September 2006

HIGHWAY DESIGN FOR PERFORMANCE

 You will be permitted to submit this HW with as many as three other CE361 students.  For every problem, identify the problem by its number and name, be clear, be concise, cite your sources, attach documentation (if appropriate), and let your methodology be known.

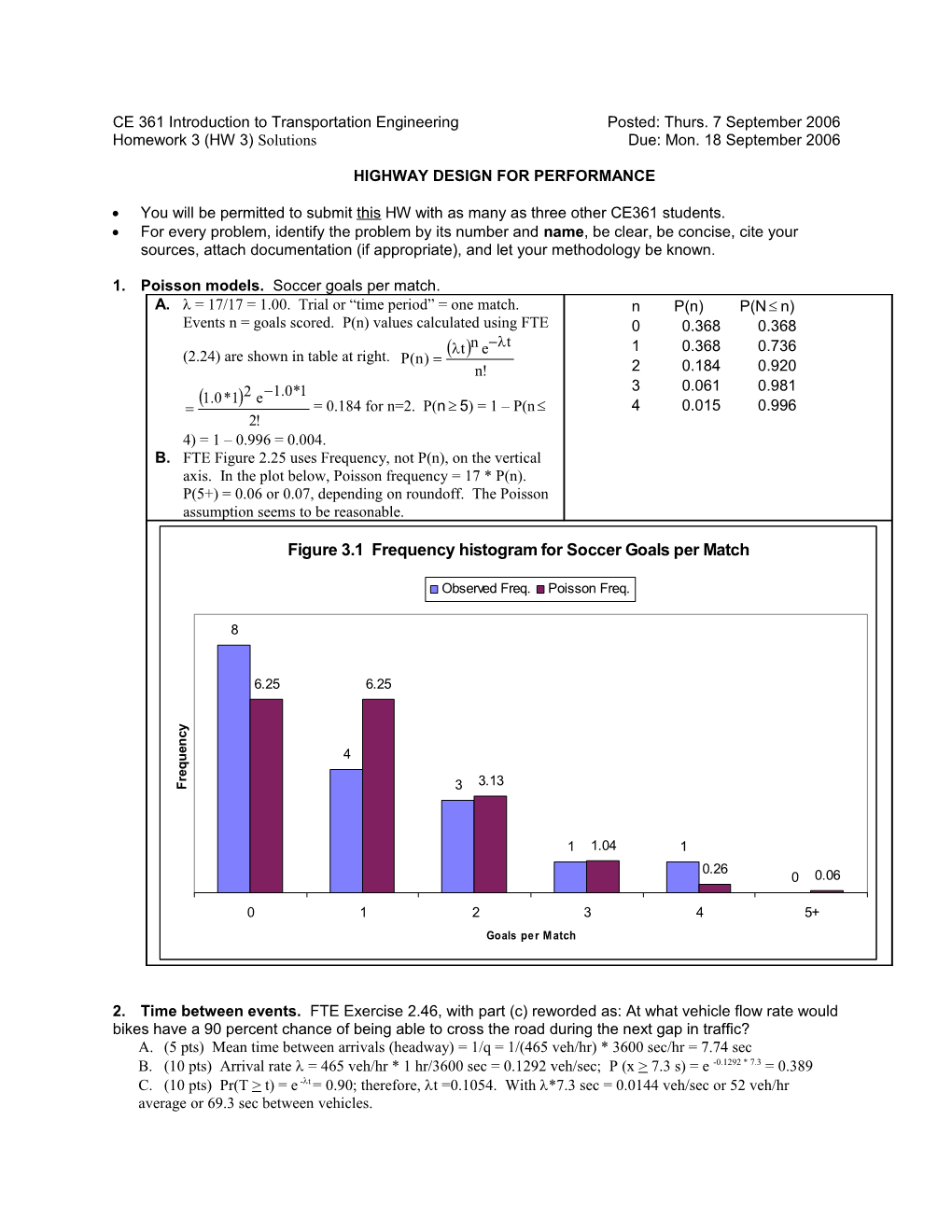
1. Poisson models. Soccer goals per match. A.  = 17/17 = 1.00. Trial or “time period” = one match. n P(n) P(N  n) Events n = goals scored. P(n) values calculated using FTE 0 0.368 0.368 tn et 1 0.368 0.736 (2.24) are shown in table at right. P(n)  n! 2 0.184 0.920 3 0.061 0.981 1.0*12 e1.0*1  = 0.184 for n=2. P(n  5) = 1 – P(n  4 0.015 0.996 2! 4) = 1 – 0.996 = 0.004. B. FTE Figure 2.25 uses Frequency, not P(n), on the vertical axis. In the plot below, Poisson frequency = 17 * P(n). P(5+) = 0.06 or 0.07, depending on roundoff. The Poisson assumption seems to be reasonable.

Figure 3.1 Frequency histogram for Soccer Goals per Match

Observed Freq. Poisson Freq.

6.25 6.25 y c n e

u 4 q e r 3.13 F 3

1 1.04 1 0.26 0 0.06

0 1 2 3 4 5+ Goals per Match

2. Time between events. FTE Exercise 2.46, with part (c) reworded as: At what vehicle flow rate would bikes have a 90 percent chance of being able to cross the road during the next gap in traffic? A. (5 pts) Mean time between arrivals (headway) = 1/q = 1/(465 veh/hr) * 3600 sec/hr = 7.74 sec B. (10 pts) Arrival rate= 465 veh/hr * 1 hr/3600 sec = 0.1292 veh/sec; P (x > 7.3 s) = e -0.1292 * 7.3 = 0.389 C. (10 pts) Pr(T > t) = e -t = 0.90; therefore, t =0.1054. With *7.3 sec = 0.0144 veh/sec or 52 veh/hr average or 69.3 sec between vehicles. 3. LOS on State Road 361. A. (10 points) Adjusted flow rate for ATS. Iter. 1 Average Travel Speed Begin with Initial vp = V/PHF = 740/0.86 = 860. 860 1st v(p) = V/PHF 1 0.93 f(G) Exhibit 20-7 fHV  (3.1) 1 PT (ET 1)  PR (ER 1) 1.9 E(T) Exhibit 20-9 1 1.1 E(R) Exhibit 20-9 fHV  = 0.932 0.932 f(HV) Equation 3.1 1 0.08(1.9 1)  0.01(1.11) 993 v(p) Equation 3.2 After one iteration, vp = 993 pc/hr. Because 993<1200, a second iteration is not needed. B. (5 points) Field measurement of speeds. 65.0 S(FM) field measured speed 1 72 V(f) observed volume fHV  = 0.842 1 (9 / 72)(2.5 1)  0.01(1.11) 0.125 P(T) 0.00 P(R) Vf FFS  SFM  0.00776 (3.4) 2.5 E(T) Exhibit 20-9 f HV 1.1 E(R) Exhibit 20-9 72  65.0  0.00776 = 65.66 mph 0.842 f(HV) Equation 3.1 0.842 65.7 FFS free-flow speed Eqn 3.4 40 50 60 C. (5 points) Average Travel Speed. The value of fnp = 1.43 comes from Exhibit 20-11 by a 2-stage linear 800 1.9 2.15 2.4 interpolation. See the table at right. By (3.5), ATS = FFS 993 1.81 – 0.00776 vp – fnp = 65.66 – (0.00776 * 993) – 1.81 = 56.14 1000 1.6 1.80 2.0 mph. This ATS corresponds to LOS A. D. (10 points) Adjusted flow rate for PTSF. After one 0.94 f(G) Exhibit 20-8 iteration, vp = 952 pc/hr. Because 952<1200, a second 1.5 E(T) Exhibit 20-10 iteration is not needed. 1.0 E(R) Exhibit 20-10 0.962 f(HV) Equation 3.1 952 v(p) Equation 3.2 50/50 E. (5 points) BPTSP and PTSF. The value of fd/np = 1.79 40 50 60 comes from Exhibit 20-12 by a 3-stage linear 800 12.3 13.2 14.1 interpolation. See the tables at right. The average of 952 11.40 1400 5.5 6.1 6.7 11.40 and 10.28 is 10.84. By (3.7), BPTSF = 100 60/40 40 50 60  0.000879 vp  0.000879*952 1  e  = 100 1 e  = 800 10.3 11.65 13.0     952 10.28 100 (1-0.433) = 56.7. By (3.8), 1400 5.4 6.25 7.1

PTSF = BPTSF + fd/np = 56.7 + 10.84 = 67.54%. This PTSF corresponds to LOS D. Despite the good ATS value, the roadway’s LOS is D. CE361 HW 3 Fall 2006 - 3 -

F. (5 points) Two-Way Two-Lane Highway Segment Worksheet. Must be attached. CE361 HW 3 Fall 2006 - 4 -

4. Interstate Backup Analysis using Queueing Diagrams. At noon, a fatal crash at mile marker 226. Flow 1625 veh/hr over two NB lanes. The previous exit was at mile marker 220. Average stopped vehicle occupies 30 feet of highway. A. (5 points) Arrival rate = 1625 vph. Time until queue backs up to mile marker 220 = 6mi *5280 ft / mi *2lanes = 1.30 hr = 77.98 minutes. 1625veh / hr *30 ft / veh B. (5 points) Service rate from U-turns = 2 veh/min * 60 min/hr = 120 veh/hr C. (15 points) Queueing diagram from noon until queue dissipation.

AC3 = 1625: Arrivals resume 3000 AC2 = 0: No new arrivals

AC1 = 1625 vph: 2500 Arrival rate until

n diversions begin o o n

0 0 : 2

1 2000

r e t f a

s e l c i

h 1500 e v

e DC2 = 4000 vph: v i t Maximum queue length Road reopens a l u

m 1000 Maximum time in queue u C

500 DC1 = 120 vph: U-turns reduce queue

0 0 50 100 150 200 250 300 350 400 Minutes after 12:00 noon

D. Estimate the following values, showing the computations: (i) (5 points) Longest vehicle delay is from (x1=24.4,y2=660) to (x3=330,y2=660), where y2 = 660 (330/60)*120= 660, x1= 1625 = 24.4 and x3 – x1 = 330 - 24.4 = 305.6 minutes.  60 CE361 HW 3 Fall 2006 - 5 -

(ii) (5 points) Longest vehicle queue is from (x2=77.98,y1=155.96) to (x2=77.98,y3=2112), where y1=77.98 min * 2 veh/min = 155.96 veh. y2-y1=2112-155.96=1956.04 veh. (iii)(5 points) When will queue dissipate? Equation for DC2 is y = (330*2) + ((4000/60)*(x-330)); Equation for AC3 is y = 2112 + ((1625/60)*(x-330)). These equations cross at x=366.62 minutes or at about 6:07 PM.

5. Queueing Analysis using Equations. Transit magnetic stripe cards. A. (5 pts) Because the “transaction time” for a Mag stripe card Cash/token turnstile is very nearly constant, and lambda 16.0 lambda 16.0 because passenger arrivals are random at mu 20.0 mu 30.0 the time scale being used (minutes), an M/D/1 queue system is most appropriate. rho 0.80 rho 0.53 B. (15 pts) Use  = 16,  = 20 or 30,  = 16/20 rho^2 0.640 rho^2 0.284 = 0.8 and 16/30 = 0.53. Calcs for mag stripe 1-rho 0.20 1-rho 0.47  2 (0.8)2 Q bar (pax) 1.600 Q bar (pax) 0.305 card: (3.15) Q   2(1 ) 2(1 0.8) W bar (min) 0.100 W bar (min) 0.019 = 1.60 passengers  0.8 (3.16) W   = 0.100 minutes = 6 seconds. Repeat for Cash/token. Q  0.305 2(1  ) 2*20*(1 0.8) passengers, W  0.019 minutes = 1.14 seconds