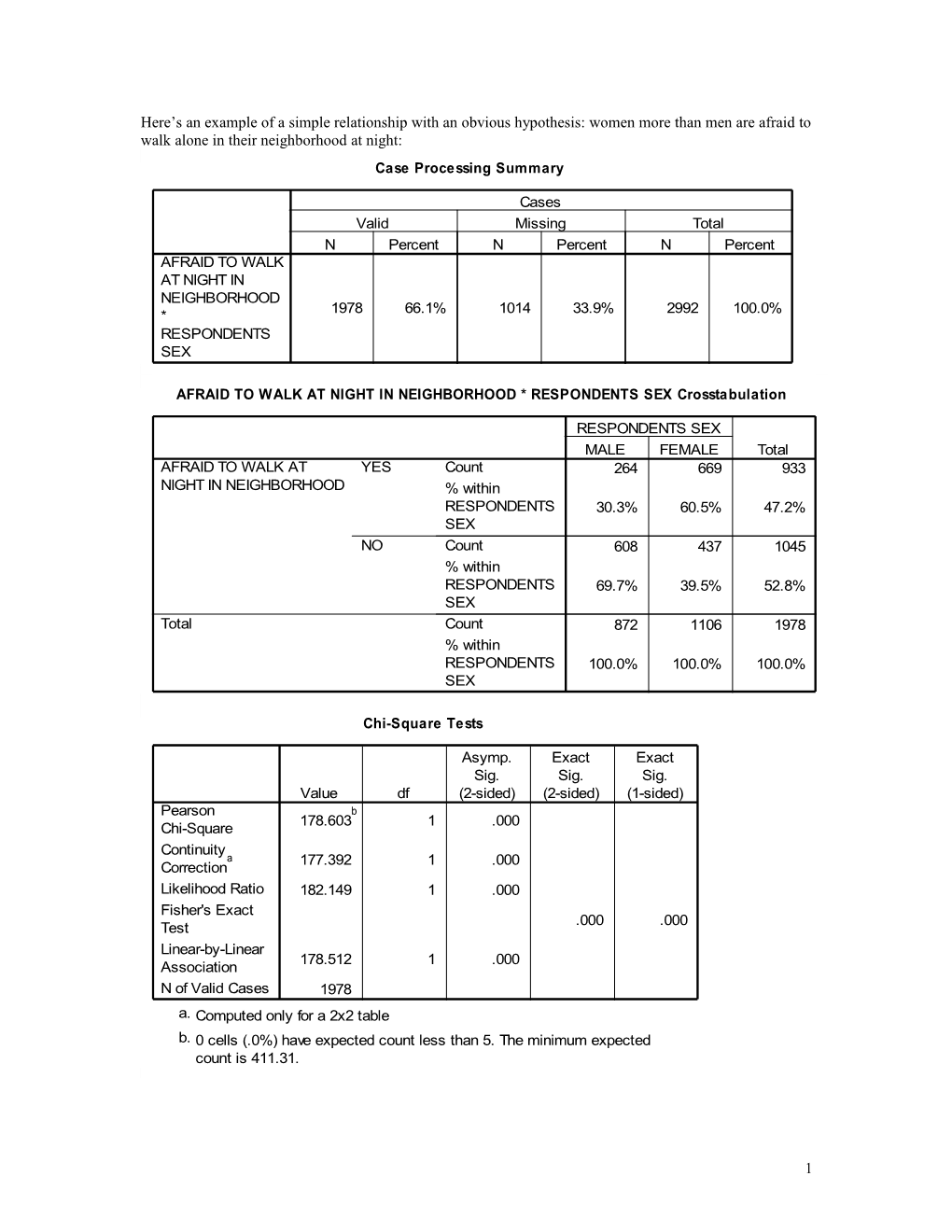
Here S an Example of a Simple Relationship with an Obvious Hypothesis: Women More Than

Here’s an example of a simple relationship with an obvious hypothesis: women more than men are afraid to walk alone in their neighborhood at night: Case Processing Summary

Cases Valid Missing Total N Percent N Percent N Percent AFRAID TO WALK AT NIGHT IN NEIGHBORHOOD 1978 66.1% 1014 33.9% 2992 100.0% * RESPONDENTS SEX

AFRAID TO WALK AT NIGHT IN NEIGHBORHOOD * RESPONDENTS SEX Crosstabulation

RESPONDENTS SEX MALE FEMALE Total AFRAID TO WALK AT YES Count 264 669 933 NIGHT IN NEIGHBORHOOD % within RESPONDENTS 30.3% 60.5% 47.2% SEX NO Count 608 437 1045 % within RESPONDENTS 69.7% 39.5% 52.8% SEX Total Count 872 1106 1978 % within RESPONDENTS 100.0% 100.0% 100.0% SEX

Chi-Square Tests

Asymp. Exact Exact Sig. Sig. Sig. Value df (2-sided) (2-sided) (1-sided) Pearson b 178.603 1 .000 Chi-Square Continuity a 177.392 1 .000 Correction Likelihood Ratio 182.149 1 .000 Fisher's Exact .000 .000 Test Linear-by-Linear 178.512 1 .000 Association N of Valid Cases 1978 a. Computed only for a 2x2 table b. 0 cells (.0%) have expected count less than 5. The minimum expected count is 411.31.

1 Symmetric Measures

Asymp. Approx. Value Std. Errora Approx. Tb Sig. Ordinal by Ordinal Gamma -.558 .033 -14.075 .000 N of Valid Cases 1978

a. Not assuming the null hypothesis. b. Using the asymptotic standard error assuming the null hypothesis.

We might want now to introduce a control variable to see if other variables affect the original hypothesis. Let’s try ownership of a gun. What’s your hypothesis? Here’s the results: Case Processing Summary

Cases Valid Missing Total N Percent N Percent N Percent AFRAID TO WALK AT NIGHT IN NEIGHBORHOOD * 1974 66.0% 1018 34.0% 2992 100.0% RESPONDENTS SEX * HAVE GUN IN HOME

2 AFRAID TO WALK AT NIGHT IN NEIGHBORHOOD * RESPONDENTS SEX * HAVE GUN IN HOME Crosstabulation

HAVE GUN RESPONDENTS SEX IN HOME MALE FEMALE Total YES AFRAID TO WALK AT YES Count 108 209 317 NIGHT IN NEIGHBORHOOD % within RESPONDENTS 24.6% 56.3% 39.1% SEX NO Count 331 162 493 % within RESPONDENTS 75.4% 43.7% 60.9% SEX Total Count 439 371 810 % within RESPONDENTS 100.0% 100.0% 100.0% SEX NO AFRAID TO WALK AT YES Count 153 455 608 NIGHT IN NEIGHBORHOOD % within RESPONDENTS 36.3% 62.7% 53.0% SEX NO Count 268 271 539 % within RESPONDENTS 63.7% 37.3% 47.0% SEX Total Count 421 726 1147 % within RESPONDENTS 100.0% 100.0% 100.0% SEX REFUSED AFRAID TO WALK AT YES Count 2 5 7 NIGHT IN NEIGHBORHOOD % within RESPONDENTS 20.0% 71.4% 41.2% SEX NO Count 8 2 10 % within RESPONDENTS 80.0% 28.6% 58.8% SEX Total Count 10 7 17 % within RESPONDENTS 100.0% 100.0% 100.0% SEX

3 Chi-Square Tests

Asymp. Exact Exact HAVE GUN Sig. Sig. Sig. IN HOME Value df (2-sided) (2-sided) (1-sided) YES Pearson b 85.003 1 .000 Chi-Square Continuity a 83.676 1 .000 Correction Likelihood Ratio 86.157 1 .000 Fisher's Exact .000 .000 Test Linear-by-Linear 84.898 1 .000 Association N of Valid Cases 810 NO Pearson c 74.164 1 .000 Chi-Square Continuity a 73.111 1 .000 Correction Likelihood Ratio 74.809 1 .000 Fisher's Exact .000 .000 Test Linear-by-Linear 74.100 1 .000 Association N of Valid Cases 1147 REFUSED Pearson d 4.496 1 .034 Chi-Square Continuity a 2.624 1 .105 Correction Likelihood Ratio 4.651 1 .031 Fisher's Exact .058 .052 Test Linear-by-Linear 4.232 1 .040 Association N of Valid Cases 17 a. Computed only for a 2x2 table b. 0 cells (.0%) have expected count less than 5. The minimum expected count is 145.19. c. 0 cells (.0%) have expected count less than 5. The minimum expected count is 197.84. d. 3 cells (75.0%) have expected count less than 5. The minimum expected count is 2.88.

4 Symmetric Measures

HAVE GUN Asymp. Approx. IN HOME Value Std. Errora Approx. Tb Sig. YES Ordinal by Ordinal Gamma -.596 .049 -9.616 .000 N of Valid Cases 810

NO Ordinal by Ordinal Gamma -.493 .048 -8.825 .000 N of Valid Cases 1147

REFUSED Ordinal by Ordinal Gamma -.818 .190 -2.368 .018 N of Valid Cases 17

a. Not assuming the null hypothesis. b. Using the asymptotic standard error assuming the null hypothesis.

Here’s another example. The theory of relative deprivation says that people who are blocked from success and gratification in the secular society are more likely to turn to religion as an alternative source of comfort and gratification. Because the US is largely a white, male-dominated society and so there should be a higher commitment to religion among women than men. Here’s the data: Case Processing Summary

Cases Valid Missing Total N Percent N Percent N Percent STRENGTH OF AFFILIATION * 2878 96.2% 114 3.8% 2992 100.0% RESPONDENTS SEX

5 STRENGTH OF AFFILIATION * RESPONDENTS SEX Crosstabulation

RESPONDENTS SEX MALE FEMALE Total STRENGTH OF STRONG Count 403 699 1102 AFFILIATION % within RESPONDENTS 32.6% 42.6% 38.3% SEX NOT VERY Count 552 636 1188 STRONG % within RESPONDENTS 44.6% 38.8% 41.3% SEX SOMEWHAT Count 127 187 314 STRONG % within RESPONDENTS 10.3% 11.4% 10.9% SEX NO Count 155 119 274 RELIGION % within RESPONDENTS 12.5% 7.3% 9.5% SEX Total Count 1237 1641 2878 % within RESPONDENTS 100.0% 100.0% 100.0% SEX

Chi-Square Tests

Asymp. Sig. Value df (2-sided) Pearson a 45.832 3 .000 Chi-Square Likelihood Ratio 45.816 3 .000 Linear-by-Linear 30.791 1 .000 Association N of Valid Cases 2878 a. 0 cells (.0%) have expected count less than 5. The minimum expected count is 117.77.

Symmetric Measures

Asymp. Approx. Value Std. Errora Approx. Tb Sig. Ordinal by Ordinal Gamma -.168 .030 -5.567 .000 N of Valid Cases 2878

a. Not assuming the null hypothesis. b. Using the asymptotic standard error assuming the null hypothesis.

6 Indeed, women have a stronger religious feeling than men. However, what happens when we control for income. For men and women with equal amounts of income, or women in higher income categories, are the results the same? Here’s the answer:

Case Processing Summary

Cases Valid Missing Total N Percent N Percent N Percent STRENGTH OF AFFILIATION * 2548 85.2% 444 14.8% 2992 100.0% RESPONDENTS SEX * INCOME

7 STRENGTH OF AFFILIATION * RESPONDENTS SEX * INCOME Crosstabulation

RESPONDENTS SEX INCOME MALE FEMALE Total $24,999 or less STRENGTH OF STRONG Count 124 271 395 AFFILIATION % within RESPONDENTS 31.2% 42.1% 38.0% SEX NOT VERY Count 177 253 430 STRONG % within RESPONDENTS 44.6% 39.3% 41.3% SEX SOMEWHAT Count 32 70 102 STRONG % within RESPONDENTS 8.1% 10.9% 9.8% SEX NO Count 64 49 113 RELIGION % within RESPONDENTS 16.1% 7.6% 10.9% SEX Total Count 397 643 1040 % within RESPONDENTS 100.0% 100.0% 100.0% SEX $25,000-50,000 STRENGTH OF STRONG Count 149 178 327 AFFILIATION % within RESPONDENTS 36.6% 40.6% 38.7% SEX NOT VERY Count 175 176 351 STRONG % within RESPONDENTS 43.0% 40.2% 41.5% SEX SOMEWHAT Count 43 53 96 STRONG % within RESPONDENTS 10.6% 12.1% 11.4% SEX NO Count 40 31 71 RELIGION % within RESPONDENTS 9.8% 7.1% 8.4% SEX Total Count 407 438 845 % within RESPONDENTS 100.0% 100.0% 100.0% SEX $50,000+ STRENGTH OF STRONG Count 92 147 239 AFFILIATION % within RESPONDENTS 28.9% 42.6% 36.0% SEX NOT VERY Count 148 138 286 STRONG % within RESPONDENTS 46.5% 40.0% 43.1% SEX SOMEWHAT Count 37 33 70 STRONG % within 8 RESPONDENTS 11.6% 9.6% 10.6% SEX NO Count 41 27 68 RELIGION % within RESPONDENTS 12.9% 7.8% 10.3% SEX Total Count 318 345 663 % within RESPONDENTS 100.0% 100.0% 100.0% SEX Chi-Square Tests

Asymp. Sig. INCOME Value df (2-sided) $24,999 or less Pearson a 27.645 3 .000 Chi-Square Likelihood Ratio 27.306 3 .000 Linear-by-Linear 16.990 1 .000 Association N of Valid Cases 1040 $25,000-50,000 Pearson b 3.625 3 .305 Chi-Square Likelihood Ratio 3.628 3 .305 Linear-by-Linear 1.632 1 .201 Association N of Valid Cases 845 $50,000+ Pearson c 15.043 3 .002 Chi-Square Likelihood Ratio 15.153 3 .002 Linear-by-Linear 12.666 1 .000 Association N of Valid Cases 663 a. 0 cells (.0%) have expected count less than 5. The minimum expected count is 38.94. b. 0 cells (.0%) have expected count less than 5. The minimum expected count is 34.20. c. 0 cells (.0%) have expected count less than 5. The minimum expected count is 32.62.

Symmetric Measures

Asymp. Approx. INCOME Value Std. Errora Approx. Tb Sig. $24,999 or less Ordinal by Ordinal Gamma -.198 .050 -3.890 .000 N of Valid Cases 1040

$25,000-50,000 Ordinal by Ordinal Gamma -.067 .056 -1.195 .232 N of Valid Cases 845

$50,000+ Ordinal by Ordinal Gamma -.235 .060 -3.813 .000 N of Valid Cases 663

a. Not assuming the null hypothesis. b. Using the asymptotic standard error assuming the null hypothesis.