Supplementary material: single neuron models
A.V. Chizhov1, E.Yu. Smirnova1, K.Kh. Kim2, A.V. Zaitsev2
1A.F.Ioffe Physical-Technical Institute of the Russian Academy of Sciences, Saint-Petersburg 2Sechenov Institute of Evolutionary Physiology and Biochemistry of the Russian Academy of Sciences, Saint-Petersburg
The individual models, taken from literature or constructed, are listed below. All voltage values are given in millivolts; time values are in milliseconds. The input is specified by two values of u and s, the voltage-independent input current and conductance, respectively, thus the external ext voltage-dependent current is I u s(V Vus ) with Vus 65 mV .
Model 1. Leaky integrate-and-fire (LIF) model with fixed threshold.
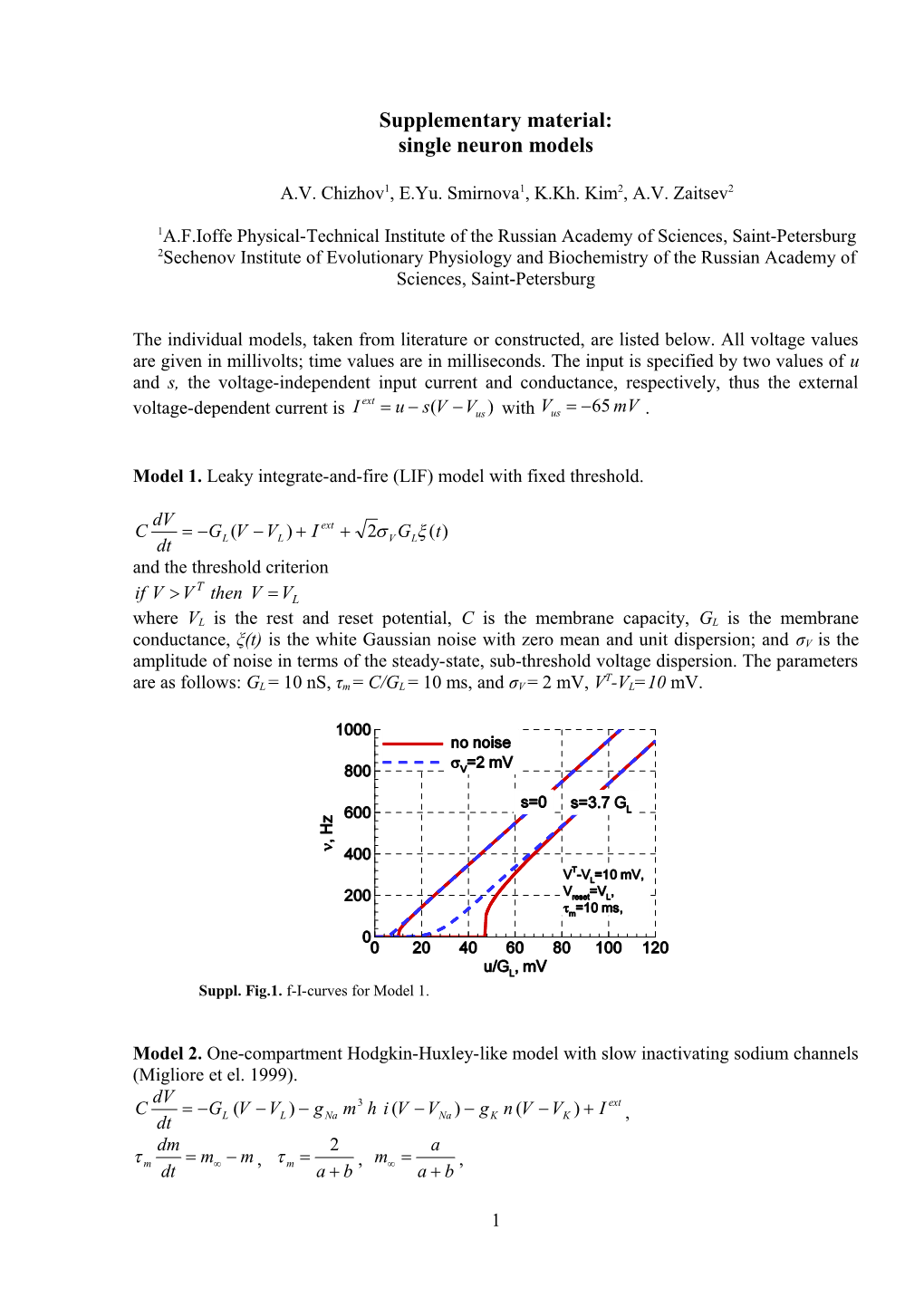
dV C G (V V ) I ext 2 G (t) dt L L V L and the threshold criterion T if V V then V VL where VL is the rest and reset potential, C is the membrane capacity, GL is the membrane conductance, ξ(t) is the white Gaussian noise with zero mean and unit dispersion; and σV is the amplitude of noise in terms of the steady-state, sub-threshold voltage dispersion. The parameters T are as follows: GL = 10 nS, τm = C/GL = 10 ms, and σV = 2 mV, V -VL=10 mV.
Suppl. Fig.1. f-I-curves for Model 1.
Model 2. One-compartment Hodgkin-Huxley-like model with slow inactivating sodium channels (Migliore et el. 1999).
dV 3 ext C GL (V VL ) g Na m h i (V VNa ) gK n (V VK ) I , dt dm 2 a m m , , m , m dt m a b a b
1 0.4(V 30) 0.124(V 30) a , b , if h 0.02 then h 0.02 , (exp((V 30) /7.2) 1) (exp((V 30) / 7.2) 1) dh 2 1 h h , , h , h dt h a b 1 exp(V 50) / 4) 0.03(V 45) 0.01(V 45) a , b , if h 0.5 then h 0.5 , (exp((V 45) /1.5) 1) (exp((V 45) /1.5) 1) di 3000b 1 0.5exp((V 58) / 2) i i , , i , i dt i 1 a 1 exp(V 58) / 2) a exp(0.45(V 60)) , b exp(0.09(V 60)) , if i 10 then i 10 , dn 50b 1 n n , , n , n dt n 1 a 1 a a exp(0.11(V 13)) , b exp(0.08(V 13)) , if n 2 then n 2 .
C 27 pF , GL 1.2nS , gNa 874nS , gK 273nS ,
VL 65.4mV , VNa 55mV , VK 72mV .
Suppl. Fig.2. Model 2: spike shape and phase-space plot in response to current step stimulation with u = 9.1 pA, starting at t=0.
Model 3. One-compartment reduction of the model (Borg-Graham 1999) with 4-state Markov approximation of sodium channels, where the effects of calcium channels were approximated by the AHP-channel. Described by Chizhov and Graham (2007): dV C = I I I I I I I G (V V ) I ext , (1) dt Na DR A M H L AHP L L Different types of ionic currents were inserted, including the leak current, IL , the fast sodium current, INa , the voltage-dependent potassium currents responsible for spike repolarization, IDR and I A , the voltage-dependent potassium current that contributes to spike frequency adaptation, IM , the voltage-dependent cation current, IH , and calcium-dependent potassium current that also contributes to spike frequency adaptation, I AHP . The approximating formulas for the currents INa , IDR , I A , IM and IH were adapted from [Graham (1999)]; the approximation for I AHP was taken from [Kopel (2000)]. 2 The sodium current INa
I Na (t) = gNa x1(t)(V (t) VNa ), (2)
x1 x2 x3 x4 = 1, (3) 4 4 dxi = Aj,i x j xi Ai, j , i = 1,2,3 (4) dt j=0, ji j=0, j i
1 1,3 1,4 A1,2 = 3 ms , A1,3 = f1 (V ), A1,4 = f1 (V ), 2,3 A2,1 = 0, A2,3 = f2 (V ), A2,4 = 0, 3,1 3,4 A3,1 = f1 (V ), A3,2 = 0, A3,4 = f2 (V ), 4,1 A4,1 = f1 (V ), A4,2 = 0, A4,3 = 0
1 V V i, j f i, j (V ) = i, j 1/exp 1/2 , 1 min i, j k 1 1 i, j i, j i, j i, j i, j 1 V V1/2 f2 (V ) = min ( max min ) exp i, j , k Note that there is an implicit coefficient of the exponential term of 1/ms in the equations i, j i, j for f1 (V ) and f2 (V ) . 1,3 1,3 1,3 min = 1/3 ms, V1/2 = 51 mV , k = 2 mV , 1,4 1,4 1,4 min = 1/3 ms, V1/2 = 57 mV , k = 2 mV , 2,3 2,3 2,3 2,3 min = 1 ms, V1/2 = 53 mV , k = 1 mV , max = 100 ms, 3,1 3,1 3,1 min = 1/3 ms, V1/2 = 42 mV , k = 1 mV , 3,4 3,4 3,4 3,4 min = 1 ms, V1/2 = 60 mV , k = 1 mV , max = 100 ms, 4,1 4,1 4,1 min = 1/3 ms, V1/2 = 51 mV , k = 1 mV ,
The voltage-dependent potassium current IDR
IDR (t) = gDR x(t) y(t) (V (t) VDR ), (5)
dx dy = x (V ) x (V ), = y (V ) y (V ) dt x dt y x = 1/(a b) 0.8 ms; x = a/(a b), a = 0.17exp((V 5) 0.090) ms 1, b = 0.17exp((V 5) 0.022) ms 1,
y = 300 ms, y = 1/(1 exp((V 68) 0.038));
The voltage-dependent potassium current I A 4 3 I A(t) = g A x (t) y (t) (V (t) VA ), (6)
dx dy = x (V ) x (V ), = y (V ) y (V ) dt x dt y 3 x = 1/(ax bx ) 1 ms; x = ax/(ax bx ), 1 ax = 0.08exp((V 41) 0.089) ms , 1 bx = 0.08exp((V 41) 0.016) ms ,
y = 1/(ay by ) 2 ms; y = ay/(ay by ), 1 ay = 0.04 exp((V 49) 0.11) ms , 1 by = 0.04 ms ;
The voltage-dependent potassium current IM
2 IM (t) = gM x (t) (V (t) VM ), (7)
dx = x (V ) x (V ), dt x x = 1/(a b) 8 ms, x = a/(a b), a = 0.003exp((V 45) 0.135) ms 1, b = 0.003exp((V 45) 0.090) ms 1;
The cation current IH
IH (t) = gH y(t) (V (t) VH ), (8)
dy = y (V ) y (V ), dt y 1 y = 180 ms, y = 1/(1 exp((V 98) 0.075)) ms ;
The adaptation current I AHP
I AHP (t) = g AHP w(t) (V (t) VAHP ), (9)
dw = w (V ) w (V ), dt w w = 4005/(3.3exp((V 35)/20) exp((V 35)/20)) ms,
w = 1/(1 exp((V 35)/10)); where the reversal potentials and maximum conductances are VDR = 70 mV , VA = 70 mV , VM = 80 mV ,
VH = 17 mV , VAHP = 70 mV ,
gNa = 1.2 S, gDR = 0.4 S, g A = 2.3 S,
gM = 0.4 S, gH = 0.003 S, g AHP = 0.32 S,
GL = 0.02 S (i.e. m = 14.4 ms),
VL = 58.5 mV (i.e. Vrest = 65 mV ),
4 Suppl. Fig.3. Model 3: spike trains (top), spike shape (bottom left) and phase-space plot (bottom right) in response to current step stimulation, starting at t=0. Stimulus amplitude for the bottom plots is u = 317 pA.
5 Model 4. One-compartment Hodgkin-Huxley-like model (Migliore et el. 1999) with two sodium channel subtypes distinguished by a shift (14 mV) of the activation and inactivation characteristics for the second channel. dV 3 ~ ~ 3 ~ ~ ext C GL (V VL ) g Na m h i (V VNa ) g Na m h i (V VNa ) g K n (V VK ) I , dt ~ dm ~ 2 a m m , , m , m dt m a b a b 0.4(V V 30) 0.124(V V 30) a , b , (exp((V V 30) / 7.2) 1) (exp((V V 30) / 7.2) 1) if h 0.02 then h 0.02 , ~ dh ~ 2 1 h h , h , h , h dt a b 1 exp(V V 50) / 4) 0.03(V V 45) 0.01(V V 45) a , b , (exp((V V 45) /1.5) 1) (exp((V V 45) /1.5) 1) if h 0.5 then h 0.5, ~ di ~ 3000b 1 0.5exp((V 58) / 2) i i , i , i , i dt 1 a 1 exp(V 58) / 2) a exp(0.45(V 60)) , b exp(0.09(V 60)) , if i 10 then i 10 . ~ V 14mV , gNa 437nS , gNa 437nS . The rest parameters and equations are the same as in Model 2.
6 Suppl. Fig.4. Model 4: top, f-I curves; bottom, spike shape and phase-space plot in response to current step stimulation with u = 14.1 pA, starting at t=0.
Model 5. Model 3, but with two sodium channel subtypes distinguished by a shift (14 mV) of the transition characteristics for the second channel. Below, the second channel current, conductance etc. are marked by tilde. dV ~ C = I I I I I I I I G (V V ) I ext , dt Na Na DR A M H L AHP L L ~ ~ ~ I Na (t) = gNa x1(t)(V (t) VNa ), (2)
x1 x2 x3 x4 = 1, (3) 4 4 dxi = Aj,i x j xi Ai, j , i = 1,2,3 (4) dt j=0, ji j=0, j i
1 1,3 1,4 A1,2 = 3 ms , A1,3 = f1 (V V ), A1,4 = f1 (V V ),
7 2,3 A2,1 = 0, A2,3 = f2 (V V ), A2,4 = 0, 3,1 3,4 A3,1 = f1 (V V ), A3,2 = 0, A3,4 = f2 (V V ), 4,1 A4,1 = f1 (V V ), A4,2 = 0, A4,3 = 0, ~ V 14mV , gNa 1S , gNa 1S . The rest parameters and equations are the same as in Model 2.
Suppl. Fig.5. Model 5: top, f-I curves; bottom, spike shape and phase-space plot in response to current step stimulation with u = 322 pA, starting at t=0.
Model 6. One-compartment, Hodgkin-Huxley-based but reduced to threshold model with slow inactivating sodium channels (Fernandez and White 2010). dV C g m h3 (V V ) g (V V ) I ext dt Na Na L L 1 m 1 exp((V 30) / 4) ,
8 dh h h 1 , h dt h 1 exp((V 52) / 2) if V 15mV then V VL 2 2 2 C 1.5F / cm , gNa 6mS / cm , gL 0.03mS / cm , VNa 50mV , VL 65mV ,
h 200ms .
Suppl. Fig.6. Model 6: top, f-I curves; bottom, spike shape and phase-space plot in response to current step stimulation with u = 0.73 μA/cm2, starting at t=0.
Model 7. One-compartment model with Markov, 26-state approximation of sodium channels (Milescu et al. 2010), fitted to experimental data obtained at room temperature. The rest ionic channels are from Model 3.
The schematic of the model of Na-channels is given in Suppl. Fig.7A,B.
A
9 B
C
Suppl. Fig.7. Model 7: Na channel kinetic model (extracted from [Milescu et al. 2010]). Model has two gating modes, differing only in their slow inactivation properties. Channels reside mostly in mode I during slow spiking, with a fraction switching to mode II during fast spiking. Rates were
exponential functions of voltage ( k k0 exp(k1 V ) ). The notations for the rates are given in A and B. C, spike shape and phase-space plot in response to current step stimulation with u = 690 pA, starting at t=0.
Numerical values for the rates and maximum conductance are given below: for m : k0= 5.254, k1= 0.01474; for m: k0= 0.3454, k1= -0.08526; for : k0= 85.07, k1=
0.005784; for : k0= 5.895, k1= -0.01043; for ’ : k0= 25.45, k1= 0.005784; for ’ : k0= 26.06, k1= -0.01043; for h: k0= 0.01068, k1= -0.04270; for h: k0= 0.05954, k1= 0.02803; for ho: k0=
0.004182, k1= -0.04270; for ho: k0= 1.805, k1= 0.02803; a= 0.71098; b= 8.1799; for s : k0= -5 5.987×10 , k1= -0.06819; for s : k0= 0.4260, k1= 0.01496; for s2 : k0= 0.01876, k1= 0.01534; for s2 : k0= 0.3355, k1= -0.02956; for c : k0= 0.03731, k1= 0.1111; for c : k0= 0.001808, k1=
0.01301; for o : k0= 1.059, k1= 0.08020; for o : k0= 0.05132, k1= -0.01791; g Na = 2.6 S . The model showed stationary spiking regime only in very limited range of stimulation parameters
10 and only without the adaptation channels, i.e. with gM g AHP 0 . That is why, the f-I-curves have not been plotted for the model.
Model 8. One-compartment model with Markov, 12-state approximation of sodium channels (Carter et al. 2010), fitted to experimental data obtained at 37 oC. The rest ionic channels are from Model 3.
The schematic of the model of Na-channels is given in Suppl. Fig.7B. Numerical values for the rates and maximum conductance are given below: for m : k0= 250, k1= 1/24; for m: k0= 12, k1= -1/24; = 250; = 60; ’= ; ’=; h= 2; h=
0.01; ho= 0.05; ho= 8; a= 2.51; b= 5.32; g Na = 2.6 S .
Suppl. Fig.8. Model 8: top, f-I curves; bottom, spike shape and phase-space plot in response to current step stimulation with u = 175 pA, starting at t=0.
11 Model 9. Spatially distributed neuron, consisting of soma and axon, based on Hodgkin-Huxley- like approximations (Yu et al. 2008).
The cable equation is dV d 2V C g 2 i (t,V ) I ext , dt L dz2 m 3 where im (t,V ) gL (V VL ) gNa m h i (V VNa ) gK n (V VK ) . The boundary conditions are
V V (t,0) ext soma ri C im (t,V (t,0)) I S , z z0 t V 0 z zL a Here is the characteristic length, a is the radius of the fiber (0.5 μm), rL is the 2 gL rL intracellular resistivity (150 Ωcm), axon length L 50 m , somatic membrane area S soma 3105 cm2 . dm 1 a m m m , m , m , dt (a b)T a b 0.182(V 43) 0.124(V 43) a , b ; (exp((V 43) / 7) 1) (exp((V 43) / 7) 1) dh 1 1 h h h , h , h , dt (a b)T 1 exp(V 72) / 6.2) 0.024(V 50) 0.0091(V 75) a , b ; (exp((V 50) / 5) 1) (exp((V 75) /5) 1) dn 1 a n n n , n , n , dt (a b)T a b 0.02(V 25) 0.002(V 25) a , b ; (exp((V 25) / 9) 1) (exp((V 25) / 9) 1) 2 2 2 2 C 0.75 F / cm , gL 33 S / cm , at soma gNa 80mS / cm , gK 32 mS / cm , at axon 2 2 gNa 800mS / cm , gK 160mS / cm , 2.3 VL 70mV , VNa 50mV , VK 90mV , the temperature factor T (T 296) /10 with T=37OC.
12 Suppl. Fig.9. Model 9: spike shape and phase-space plot in response to current step stimulation with u = 1.7 μA/cm2, starting at t=0.
Model 10. Adaptive exponential integrate-and-fire model (Brette and Gerstner 2005):
T dV (V V ) / T ext C GL (V VL ) GLT e w I , dt dw w a(V VL ) w , dt
if V 15 ms then V VL , w w w , T VL 65 mV , GL 26 nS , C 370 pF , V 50.3mV , T 2 mV , w 14.4 ms , a 4 nS , w 0.0805 nA
13 Suppl. Fig.10. Model 10: spike train (top), spike shape (bottom left) and phase-space plot (bottom right) in response to current step stimulation, starting at t=0. Stimulus amplitude is 4μA/cm2 for the top plot and u = 1.15 μA/cm2 for the bottom plots.
Model 11. Exponential integrate-and-fire model with spike-dependent parameters (Badel et al. 2008).
T dV (V V ) / T ext C GL (V VL ) GLT e I , dt
0 (t tk ) / 32.8 (t tk ) / 42.9 VL VL 49.8 e 42.7 e ,
0 (ttk ) / 20 GL GL 16 e
T T (t tk ) /14 V V0 18.4 e
if V 15 ms then V VL ,
tk - spike time moment; 0 0 T VL 57 mV , GL 18 nS , C 370 pF , V0 42 mV , T 1.51 mV .
14 Suppl. Fig.11. Model 11: spike train (top), spike shape (bottom left) and phase-space plot (bottom right) in response to current step stimulation, starting at t=0. Stimulus amplitude is 4μA/cm2 for the top plot and u = 1.15 μA/cm2 for the bottom plots.
15 Model 12. Model 3, but with a new semi-phenomenological model of sodium channels with 3 Markov states (closed (C), open (O), and inactivated (I)) and the dynamic, I-dependent threshold of C-to-O transition (see Sections 2.2.2 and 3.3).
Suppl. Fig.12. Model 12: spike shape and phase-space plot in response to current step stimulation with u = 320 pA, starting at t=0.
Model 13. LIF model with dynamic threshold. The model description and simulation results are given in Sections 2.2.3 and 3.4).
The models 1-12 were programmed in Delphi-7 environment. The source code and executive file are available from the webpage http://www.ioffe.ru/CompPhysLab/AntonV3.html.
16