Solution
Case 1
There are two variables in the question, shape and number of trees. Number of trees is the dependent variable. The dependent variable is quantitative. The shape is the independent variable. The independent variable is categorical. There are three categories: square, round, rectangular. The model Y~X now suggests ANOVA test.
Assumption checking:
1.The four samples are independent.
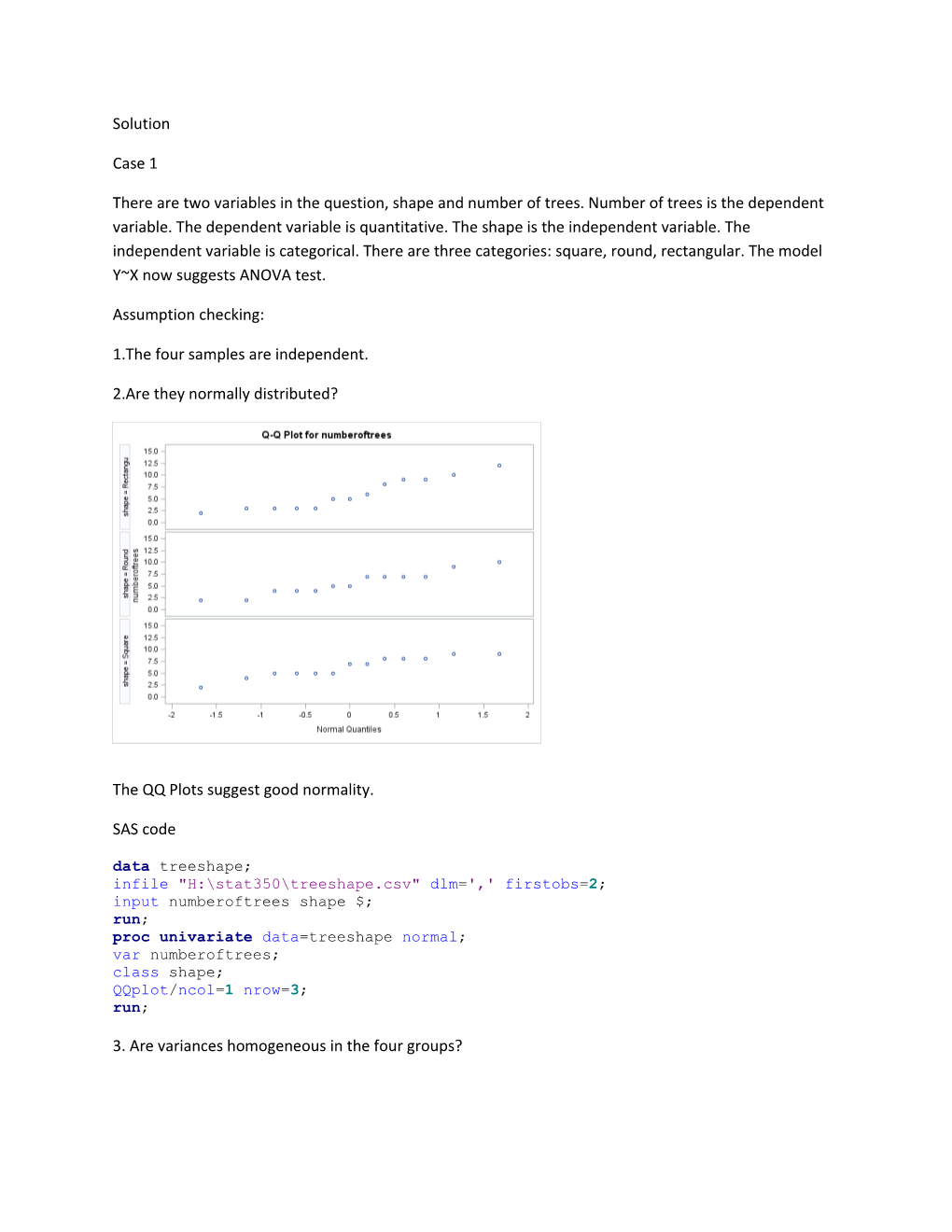
2.Are they normally distributed?
The QQ Plots suggest good normality.
SAS code data treeshape; infile "H:\stat350\treeshape.csv" dlm=',' firstobs=2; input numberoftrees shape $; run; proc univariate data=treeshape normal; var numberoftrees; class shape; QQplot/ncol=1 nrow=3; run;
3. Are variances homogeneous in the four groups? The boxplots suggest the variances are not equal. To make sure this, we run levene’s test for homogeneity.
example of one-way ANOVA
The ANOVA Procedure Levene's Test for Homogeneity of numberoftrees Variance ANOVA of Squared Deviations from Group Means Sourc DF Sum of Squares Mean Square F Pr > F e Value shape 2 223.4 111.7 2.23 0.1220 Error 36 1802.6 50.0735
Welch's ANOVA for numberoftrees Source DF F Value Pr > F shape 2.0000 0.28 0.7550 Error 23.3913
Since the p-value (0.122) is big enough, the s for each group are the same.
SAS code proc boxplot data=treeshape; plot numberoftrees * shape/boxstyle=skeletal; run; proc ANOVA data=treeshape; title example of one-way ANOVA; class shape; model numberoftrees = shape; means shape / hovtest welch; run;
The suggested method now is ANOVA. Output and the source code are shown below.
The ANOVA Procedure Dependent Variable: numberoftrees Source D Sum of Squares Mean Square F Pr > F F Value Model 2 3.1282051 1.5641026 0.22 0.8035 Error 36 255.8461538 7.1068376 Corrected Total 38 258.9743590
SAS code proc anova data=treeshape; class shape; model numberoftrees=shape;
Conclusion: According to the p-value (0.8035), the ANOVA test is not significant. Hence, the shape does not effect on the number of trees. Case 2
Y(categorical)~X(categorical), the model suggests contingency test. data case2; input improvement $ drug $ count; datalines; yes clozapine 61 yes haloperidol 51 no clozapine 102 no haloperidol 108 ; proc freq data=case2; tables improvement*drug/chisq nocol norow nopercent expected; weight count; run;
The FREQ Procedure
Table of improvement by drug
improvement drug
Frequency‚ Expected ‚clozapin‚haloperi‚ Total ƒƒƒƒƒƒƒƒƒˆƒƒƒƒƒƒƒƒˆƒƒƒƒƒƒƒƒˆ no ‚ 102 ‚ 108 ‚ 210 ‚ 106.3 ‚ 103.7 ‚ ƒƒƒƒƒƒƒƒƒˆƒƒƒƒƒƒƒƒˆƒƒƒƒƒƒƒƒˆ yes ‚ 61 ‚ 51 ‚ 112 ‚ 56.696 ‚ 55.304 ‚ ƒƒƒƒƒƒƒƒƒˆƒƒƒƒƒƒƒƒˆƒƒƒƒƒƒƒƒˆ Total 163 159 322
The expected frequency is 106.3, 103.7, 56.696 and 55.304, they are all greater than 5. Other wise Fisher’s exact test should be used.
Statistics for Table of improvement by drug
Statistic DF Value Prob ƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒ Chi- Square 1 1.0148 0.3138 Likelihood Ratio Chi- Square 1 1.0158 0.3135 Continuity Adj. Chi- Square 1 0.7927 0.3733 Mantel- Haenszel Chi- Square 1 1.0116 0.3145 Phi Coefficient - 0.0561 Contingency Coefficient 0.0560 Cramer's V - 0.0561 The p-value = 0.3138 >0.5, the contingency test suggests there is an insignificant association between patient’s improvement and the drug used.
Case 3
There are two variables group and hour of pain relief. Group is the independent variable. The independent variable is categorical. There are two categories: one is demerol, the other is experimental drug. The hour of pain relief is dependent variable. The dependent variable is quantitative. We should begin with two sample t-test for this case.
Assumption checking:
1. The two samples are independent.
2. Are the two samples normally distributed?
First, we plot a QQ plot.
The UNIVARIATE Procedure
The QQ plots do not suggest the normality, so we use the tests for normality.
Group 1:
Tests for Normality Test Statistic p Value Shapiro-Wilk W 0.764281 Pr < W 0.0178 Kolmogorov- D 0.247528 Pr > D >0.1500 Smirnov Tests for Normality Test Statistic p Value Cramer-von Mises W-Sq 0.121989 Pr > W- 0.0447 Sq Anderson-Darling A-Sq 0.733319 Pr > A-Sq 0.0307 Since the p-value (0.0178) is smaller than 0.05, there is moderate evidence for nonormality.
Group 2:
Tests for Normality Test Statistic p Value Shapiro-Wilk W 0.72105 Pr < W 0.0039 Kolmogorov- D 0.372958 Pr > D <0.0100 Smirnov Cramer-von Mises W-Sq 0.216307 Pr > W- <0.0050 Sq Anderson-Darling A-Sq 1.100942 Pr > A-Sq <0.0050 Since the p-value (0.0039) is smaller than 0.01, there is strong evidence for nonnormality.
Conclusion: Since the distributions of the two samples do not follow normal distribution and the two samples are independent, we should use WMW test.
SAS code data relief; infile "H:\stat350\relief.csv." dlm=',' firstobs=2; input group $ hour; run; proc univariate data=relief normal plot; var hour; class group; qqplot/ ncol=2 nrow=1; run; proc univariate data=relief normal; qqplot hour / normal (mu=est sigma=est color=red l=1); by group; run;
Relevant WMW test output
Wilcoxon Two-Sample Test Statistic (S) 53.0000 Wilcoxon Two-Sample Test Normal Approximation Z -0.2933 One-Sided Pr < Z 0.3847 Two-Sided Pr > |Z| 0.7693
t Approximation One-Sided Pr < Z 0.3868 Two-Sided Pr > |Z| 0.7736
Exact Test One-Sided Pr <= S 0.3731 Two-Sided Pr >= |S - Mean| 0.7465 Z includes a continuity correction of 0.5.
SAS code proc npar1way data=relief wilcoxon; title "nonparametric test to compare the hours between two groups"; class group; var hour; exact wilcoxon; run;
Conclusion: Look at the Exact Test. Since the p value (0.7465) of the two sided test are bigger than 0.05, we conclude that the number of pain hour between the two groups are insignificantly different. So, Demerol is insignificantly different than the experimental drug on the effects. Case 4
Research question: Is forearm length affected by body height?
There are two variables. One is body height, the other is forearm. Both are quantitative. Body height is independent variable. Forearm is dependent variable.
The model Y~X now suggests linear regression.
Assumption checking:
1. Are body height and forearm associated linearly?
Based on the picture above, body height and forearm are linear associated.
2. Are the body height homoscedastic? The scatter plot shows randomness, no patter, and approximately the same number of points above and below the e=0 line.
SAS code data forearm; infile "H:\stat350\forearm.csv." dlm="," firstobs=2; input height forearm; run; proc reg data=forearm; model forearm=height; plot forearm * height; output out=forearm1 p=red r=resid; run; proc gplot data=forearm1; plot resid * height/vref=0 cvref=red; run;
3. Are the body heights normally distributed? QQ plot suggests the sample is normally distributed.
SAS code proc univariate data=forearm1; qqplot resid / normal (mu=est sigma=est); run;
Relevant Output for linear regression is shown below.
Parameter Estimates Variable DF Parameter Standard t Value Pr > |t| Estimate Error Intercep 1 10.33121 4.80988 2.15 0.0497 t height 1 0.09463 0.02929 3.23 0.0060
SAS code proc reg data=forearm; model forearm=height; plot forearm * height; output out=forearm1 p=red r=resid; run; proc gplot data=forearm1; Conclusion: The linear regression function is calculated as body forearm=10.333121+0.09463*height, where test for slope is significant with a ts=3.23 and p-value=0.006. Hence, the height has a significant positive linear effect on weight.