DATA ANALYSIS GUIDE-SPSS When conducting any statistical analysis, you need to get familiar with your data and perform an examination of it in order to lessen the odds of having biased results that can make all of your hard work essentially meaningless or substantially weak.
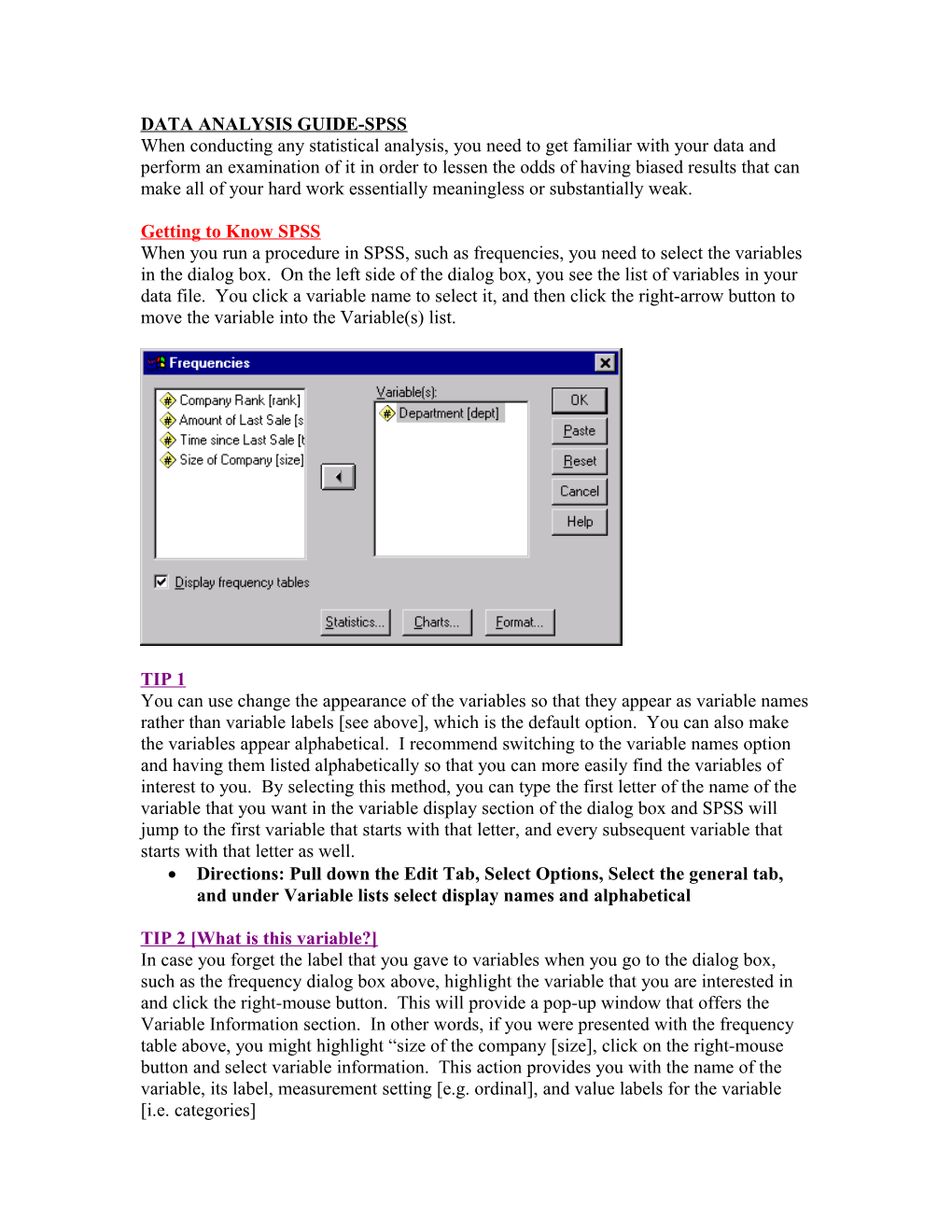
Getting to Know SPSS When you run a procedure in SPSS, such as frequencies, you need to select the variables in the dialog box. On the left side of the dialog box, you see the list of variables in your data file. You click a variable name to select it, and then click the right-arrow button to move the variable into the Variable(s) list.
TIP 1 You can use change the appearance of the variables so that they appear as variable names rather than variable labels [see above], which is the default option. You can also make the variables appear alphabetical. I recommend switching to the variable names option and having them listed alphabetically so that you can more easily find the variables of interest to you. By selecting this method, you can type the first letter of the name of the variable that you want in the variable display section of the dialog box and SPSS will jump to the first variable that starts with that letter, and every subsequent variable that starts with that letter as well. Directions: Pull down the Edit Tab, Select Options, Select the general tab, and under Variable lists select display names and alphabetical
TIP 2 [What is this variable?] In case you forget the label that you gave to variables when you go to the dialog box, such as the frequency dialog box above, highlight the variable that you are interested in and click the right-mouse button. This will provide a pop-up window that offers the Variable Information section. In other words, if you were presented with the frequency table above, you might highlight “size of the company [size], click on the right-mouse button and select variable information. This action provides you with the name of the variable, its label, measurement setting [e.g. ordinal], and value labels for the variable [i.e. categories] TIP 3 [What is this statistic?] If you are unsure of what a particular statistic is used for, then highlight the particular item, right-click on the selected statistics [e.g. mean] and you will receive a brief description of what the statistics available in the dialog box provide. If the variable is one that seems useful to you, then you select it by placing a check in the available box next to the statistic. Then click ok and you will return to the main frequencies box.
TIP 4 [What is in this output?] To obtain help on the output screen [i.e. the spss viewer], you need to double click a pivot table in order to activate it so that you can make modifications. When activated, it will appear to have “railroad track” lines surrounding it. See Table a below.
Favor or Oppose Death Penalty for Murder
Cumulative Frequency Percent Valid Percent Percent Valid Favor 1074 71.6 77.4 77.4 Oppose 314 20.9 22.6 100.0 Total 1388 92.5 100.0 Missing DK 106 7.1 NA 6 .4 Total 112 7.5 Total 1500 100.0
Once you have activated the pivot table, then you should right-click a row or column header for a pop up menu, such as the column labeled valid percent. Choose what’s this? This will bring up a pop-up window explaining what the particular column or row is addressing. If you forget to activate the pivot table and simply right-click on a column or row, you will get the following message: [Displays output. Click once to select an object (for example, so that you can copy it to the clipboard). Double-click to activate an object for editing. If the object is a pivot table, you can obtain detailed help on items within the table by right-clicking on row and column labels after the table is activated.]
If you want more than a pop-up delivers, choose results coach from the list instead of what’s this? Essentially, this will take you through a subsection of the SPSS tutorial.
Dressing Up Your Output Changing Text Activate the pivot table in the SPSS viewer [see Output screen] and then double- click on the text that you wish to change. Enter the new text and then follow the same procedure as needed. If you wish to get rid of the title, then you can select the title and then hit the delete button on your keyboard and you will obtain a table like the one below.
Changing the Number of Decimal Places Select the cell entries with too many [or too few] decimal places. From the format menu, choose Cell properties, select the number of decimal points that you want and click OK.
Showing/Hiding Cells Activate the table and then select the row or column you wish by using Ctrl-Alt- click in the column heading or row label. From the view label, choose hide. To resurrect the table at a later time, activate the table and then from the view menu, choose show all. If you’re sure that you never want to resurrect the information, then you can simply delete them and they will be permanently removed. See Table a above, which shows a table with unhidden columns. See Table b for an example of a table with hidden valid percent column.
Table b
Favor or Oppose Death Penalty for Murder
Cumulative Frequency Percent Percent Valid Favor 1074 71.6 77.4 Oppose 314 20.9 100.0 Total 1388 92.5 Missing DK 106 7.1 NA 6 .4 Total 112 7.5 Total 1500 100.0 Rearranging the rows, columns, and layers Activate the pivot table, and from the pivot menu, choose pivoting trays. A schematic representation of a pivot table appears with 3 areas [trays] labeled layer, row, and column. Colored icons in these trays represent the contents of the table, one for each variable and one for statistics. Place your mouse pointer over one of them to see what it represents and if you wish to change the structure of the table, then you can drag an icon and the table will rearrange itself. See Table b above for a pre-modification version of the table and Table c below for a post-modification version.
Table c = post-modification version of Table b
Favor or Oppose Death Penalty for Murder Valid Favor Frequency 1074 Percent 71.6 Cumulative 77.4 Percent Oppose Frequency 314 Percent 20.9 Cumulative 100.0 Percent Total Frequency 1388 Percent 92.5 Missing DK Frequency 106 Percent 7.1 NA Frequency 6 Percent .4 Total Frequency 112 Percent 7.5 Total Frequency 1500 Percent 100.0
Editing Your Charts Double click on the viewer option to open it in a new chart editor window. Note: To access some chart editing capabilities, such as identifying points on a scatterplot or changing the width of bars in a histogram, you must click an element of the chart to select it. For example, you must click any point in a scatterplot or any bar in a histogram or bar chart. You can change labels [double-click any text and substitute your own], create reference lines, and change colors, line types and sizes. When you close the Chart editor window, the original chart in the viewer updates show any changes that you made.
Using Syntax You should ALWAYS use syntax when running statistical analyses. There are 2 ways that you can do this. You can select the paste tab when you run a statistical analysis using one of the dialog boxes, such as that for frequencies. However, when you use the paste function, you have to remember to go to the newly created syntax window or one that you created in a previous session and highlight the commands if you wish the analysis to actually run. The other method is to open a new syntax file so that you can type in any commentary and syntax or copy and paste from an already existing syntax file. The syntax below is what you would receive if you did a paste command in SPSS after using a dialog box, such as that for frequencies and you would also receive this command if you did a copy and paste of prior commands in an already existing syntax or a newly created one.
FREQUENCIES VARIABLES=cappun /PIECHART PERCENT /ORDER= ANALYSIS .
Whichever method you use to create syntax, you MUST always type in commentary that explains what the command does. This ensures that you have a way of checking back to see the methodology that you used and the steps that were taken when you conducted your analysis. This is useful in case something goes wrong and you need to make corrections and just to provide you and others with a guide for how the analyses occurred in case replications need to be done. Commentary should be written in the following way when dealing with commands:
*frequencies of attitudes toward capital punishment and gun laws.*
Notice that there are asterisk at either end and that a period (.) is just before the closing asterisk. This tells the computer that this is not command text, so that while the computer may highlight it during a run of the analysis, it will not view it as command text. If you were going to combine the commentary and the command syntax in a syntax file, it would appear as you see it below. *frequencies of attitudes toward capital punishment and gun laws.*
FREQUENCIES VARIABLES=cappun /PIECHART PERCENT /ORDER= ANALYSIS .
In addition, you MUST keep a Log of the analyses that you run, which will appear in the output [SPSS viewer] file. To do this, you need to go to Edit, then options, and select the viewer tab. Under that tab, be sure that initial output state has “log” listed in the pull- down tab and that display commands in the log is checked. This ensures that the information that the program enters the text of any analysis that you do right before it displays the results of the analysis, which is another way to let yourself and others know what type of analysis you did and to evaluate whether it is the appropriate analysis and whether it has been done properly in that case. See the information just below this text for a sample.
FREQUENCIES VARIABLES=cappun /ORDER= ANALYSIS . Frequencies
Statistics
Favor or Oppose Death Penalty for Murder N Valid 1388 Missing 112
Favor or Oppose Death Penalty for Murder
Cumulative Frequency Percent Percent Valid Favor 1074 71.6 77.4 Oppose 314 20.9 100.0 Total 1388 92.5 Missing DK 106 7.1 NA 6 .4 Total 112 7.5 Total 1500 100.0
Introducing Data Typing your own data If your data aren’t already in a computer-readable SPSS format, you can enter the information directly into the SPSS Data Editor. From the menus, choose file, then new, then data, which opens the data editor in data view. If you type a number into the first cell, SPSS will label that column with the variable name VAR00001. To create your own variable names, click the variable view tab. Assigning Variable names and properties In the name column, enter a unique name for each variable in the order in which you want to enter the variables. The name must start with a letter, but the remaining part of the variable can be letters or digits. A name can’t end with a period, contain blanks or special characters, or be longer than 64 characters.
Assigning Descriptive Labels Variable Labels: Assign descriptive text to a variable by clicking the cell and then entering the label. For instance for the variable “cappun” the label says “favor or oppose death penalty for murder.” Value Labels: To label individual values, click the button in the Value column. This opens its dialog box. For cappun, the label is coded 1 = favor, 2 = oppose. The sequence of operations is to: enter the value, enter its label, click add, and repeat this process for each value. o Note: Labels for individual values are useful only for variables with a limited number of categories whose codes aren’t self-explanatory. You don’t want to attach value labels to individual ages; however, you should label the missing value codes for all variables if you use more than one code.
Assigning Missing Values To indicate which codes were used for each variable when information is not available, click in the missing column, and assign missing values. Cases with these codes will be treated differently during statistical analysis. If you don’t assign codes for missing values, even nonsensical values are accepted. A value of -1 for age would be considered a real age. The missing-value codes that you assign to a variable are called user- missing values. System-missing values are assigned by SPSS to any blank numeric cell in the Data Editor or to any calculated value that is not defined. A system-missing value is indicated with a period (.). Note: You can’t assign missing values to a string variable that is more than 8 characters in width. For string variables, uppercase and lowercase letters are treated as distinct characters. This means that if you use the code NA (not available) as a missing value code, entries coded as na will not be treated as missing. Also, if a string variable is 3 characters wide and the missing value code is only 2 characters wide, the placement of the two characters in the field of 3 affects what’s considered missing. Blanks at the end of the field (trailing blanks) are ignored in missing-value specifications. Warning: DON’T use a blank space as a missing value. Use a specific number or character to signify that I looked for this value and I don’t know what it is. DON’T use missing-value codes that are between the smallest and largest valid values, even if these particular codes don’t occur in the data.
Assigning Levels of Measurement Click in a cell in the Measure column to assign a level of measurement to each variable. You have 3 choices: nominal, ordinal, and scale. Warning 1: If you don’t specify the scale, SPSS attempts to divine it based on characteristics of the data, but its judgment in this matter is fallible. For example, string variables are always designated as nominal. In some procedures, SPSS uses different icons for the 3 types of variables. The scale on which a variable is measured doesn’t necessarily dictate the appropriate statistical analysis for a variable. For example, an ID number assigned to subjects in an experiment is usually classified as a nominal variable. If the numbers are assigned sequentially, however, they can be plotted on a scale to see if subject responses change with time. Vellemena and Wilkinson (1993) discuss the problems associated with stereotyping variables. Warning 2: Although SPSS assigns a level of measurement to each variable, this information is seldom used to guide you. SPSS will let you calculate means for nominal variables as long as they have numeric values. Certain statistical procedures don’t allow string variables in particular fields in the dialog boxes. For example, you can’t calculate the mean of a string variable.
Saving the Data File You MUST always save your data periodically so that you don’t have to start from scratch if anything goes wrong. You can also include text information in an SPSS data file by choosing utilities and data file comments, which will appear in the syntax screen. Anyone using the file can read the text associated with it. You can also elect to have the comments displayed in the output. This is similar to what you would do with your own inclusion of comments alerting what steps you are taking in your data analysis. I recommend the other way because you will already be in the syntax rather than having to switch back and forth, but this is a possible option.
* Data File Comments. PRESERVE. SET PRINT OFF. ADD DOCUMENT 'test of data file comments'. RESTORE.
Selecting Cases for Analyses If you wish to perform analyses on a subset of your cases, this command is invaluable. For instance, consider that you want to examine gender differences in support for or opposition to capital punishment. Choose select cases from the data menu and all analyses will be restricted to the cases that meet the criteria you specified. After choosing select cases, choose select if condition is satisfied and also click on the “if” tab. This will take you to a dialog box that allows you to complete the command syntax necessary to carry out the procedure. Considering the example, that I gave you, Males are coded 1 and Females are coded 2. I am interested in calculating results separately for both groups. Therefore, I click on sex under the variable list and use the arrow to put it in the box allocated for formulas. Once this variable has been transferred, I click on the = sign on the calculator provided and then on a “1” so that I inform the computer that I am only interested in selecting cases for males. Then I hit continue and go back to the original select cases dialog box where I can choose “unselected cases are filtered” or “unselected cases are deleted. If you wish to keep both males and females in the dataset, but you want to conduct separate analyses for each group, you want to choose “filtered.” If you wish to get rid of those cases that don’t meet the criterion, i.e. you want to delete the females from the data set permanently, you want to choose “deleted.” If you look at the Data Editor when Select Cases is in effect, you’ll see lines through the cases that did not meet the selection criteria [only for filtering of cases]. They won’t be included in any statistical analysis or graphical procedures.
Repeating the Analysis for Different Groups of Cases If you want to perform the same analysis for several groups of cases, choose Split File from the Data menu. A separate analysis is done for each combination of values of the variables specified in the Split File Dialog box.
SORT CASES BY sex . SPLIT FILE LAYERED BY sex .
Frequencies
Statistics
Favor or Oppose Death Penalty for Murder Male N Valid 607 Missing 34 Female N Valid 781 Missing 78
Favor or Oppose Death Penalty for Murder
Cumulative Respondent's Sex Frequency Percent Valid Percent Percent Male Valid Favor 502 78.3 82.7 82.7 Oppose 105 16.4 17.3 100.0 Total 607 94.7 100.0 Missing DK 34 5.3 Total 641 100.0 Female Valid Favor 572 66.6 73.2 73.2 Oppose 209 24.3 26.8 100.0 Total 781 90.9 100.0 Missing DK 72 8.4 NA 6 .7 Total 78 9.1 Total 859 100.0
You can also select how you want the output displayed—all output for each subgroup together or the same output for each subgroup together. SORT CASES BY sex . SPLIT FILE SEPARATE BY sex .
Frequencies
Respondent's Sex = Male
Statisticsa
Favor or Oppose Death Penalty for Murder N Valid 607 Missing 34 a. Respondent's Sex = Male
Favor or Oppose Death Penalty for Murdera
Cumulative Frequency Percent Valid Percent Percent Valid Favor 502 78.3 82.7 82.7 Oppose 105 16.4 17.3 100.0 Total 607 94.7 100.0 Missing DK 34 5.3 Total 641 100.0 a. Respondent's Sex = Male Respondent's Sex = Female
Statisticsa
Favor or Oppose Death Penalty for Murder N Valid 781 Missing 78 a. Respondent's Sex = Female Favor or Oppose Death Penalty for Murdera
Cumulative Frequency Percent Valid Percent Percent Valid Favor 572 66.6 73.2 73.2 Oppose 209 24.3 26.8 100.0 Total 781 90.9 100.0 Missing DK 72 8.4 NA 6 .7 Total 78 9.1 Total 859 100.0 a. Respondent's Sex = Female Preparing Your Data Checking Variable Definitions Using the Utilities Menu Choose utilities and then variables to get data-definition information for each variable in your data file. Make sure that all of your missing-value codes are correctly identified.
TIP 5 If you click, Go To, you find yourself in the column of the Data Editor for the selected variable if the data editor is in data view. To edit the variable information from the data editor in data view, double-click the variable name at the top of that column. This takes you to the variable view for that variable.
TIP 6 To get a listing of the information for all of the variables without having to select the variables individually, choose File, then display data file information, then working file. This lists variable information for the whole data file. The disadvantage is that you can’t quickly go back to the data editor to fix mistakes. An advantage is that codes that are defined as missing are identified, so it’s easier to check the labels.
Checking Your Case Count Eliminating Duplicate Cases If you have entered your own data, it is possible that you will enter the same case twice or even more. To oust any duplicates, choose data, then identify duplicate cases. If you entered a supposedly unique ID variable for each case, move the name of that ID variable into the Define Matching Cases By list. If it takes more than one variable to guarantee uniqueness (for example, college and student ID), move all of these variables into the list. When you click OK, SPSS checks the file for cases that have duplicate values of the ID variables.
TIP 7 DON’T automatically discard cases with the same ID number unless all of the other values also match. It’s possible that the problem is merely that a wrong ID number was entered. Adding Missing Cases Run any procedure and look at the count of the total cases processed. That’s always the first piece of output. Table d shows the summary from the Crosstabs procedure for sex by cappun.
Table d
Crosstabs
Case Processing Summary
Cases Valid Missing Total N Percent N Percent N Percent Respondent's Sex * Favor or Oppose Death 1388 92.5% 112 7.5% 1500 100.0% Penalty for Murder
You see that the data file has 1500 cases, but only 1388 have valid (nonmissing) values for the sex and cappun variables. If the count isn’t what you think it should be and if you assigned sequential numbers to cases, you can look for missing ID numbers.
Checking Your Case Count Warning: Data checking is not an excuse to get rid of data values that you don’t like. You are looking for values that are obviously in error and need to be corrected or replaced with missing values. This is not the time to deal with unusual but correct data points. You’ll deal with those during the actual data analysis phase.
Making Frequency Tables Use the frequency procedure to count the number of times each value of a variable occurs in your data. For example, how many people in the gss survey support capital punishment? You can also graph this information using pie charts, bar charts, or histograms.
TIP 8 You can acquire the information that you need for the descriptive statistics [e.g. mean, minimum, maximum] through the frequency dialog box by selecting the statistics tab and checking on those statistics of interest to you. To obtain your frequencies and descriptives, follow the instructions below. Go to Analyze, scroll down to descriptive statistics and select frequencies. Click on the variables of interests and move them into the box for analysis using the arrow shown. To obtain the descriptives, check on the statistics tab in the frequency dialog box and select the mean, minimum, maximum, and standard deviation boxes. Then click on charts and decide whether you wish to run a pie chart, a bar chart, or a histogram chart w/ a normal curve. You can only run one type of graph/chart at a time.
When conducting frequency analyses, you want to consider the following questions when reviewing the results presented in your output. Are the codes that you used for missing values labeled as missing values in the frequency table? If the codes are not labeled, go back to the data editor and specify them as missing values. Do the value labels correctly match the codes? For example, if you see that 50% of your customers are very dissatisfied with your product, make sure that you haven’t made a mistake in assigning the labels. Are all of the values in the table possible? For example, if you asked the number of times a person has been married and you see values of -2, you know that’s an error. Go back to the source and see if you can figure out what the correct values are. If you can’t, replace them with codes for missing values. Are there values that are possible, but highly unlikely? For example, if you see a subject who claims to own 11 toasters, you want to check whether the value is correct. If the value is incorrect, you’ll have to take that into account when analyzing the data. Are there unexpectedly large or small counts for any of the values? If you’re studying the relationship of highest educational degree to subscription to Web services offered by your company and you see that no one in your sample has a college degree, suspect problems.
TIP 9 To search for a particular data value for a variable, go to data view, highlight the column of the variable that you are interested in, choose edit, then find, and then type in the value that you are interested in finding.
Looking At the Distribution of Values For a scale variable with too many values for a frequency table [e.g. income in dollars], you need different tools for checking the data values because counting how often different values occur isn’t useful anymore.
Are the smallest and largest values sensible? You don’t want to look solely at the single largest and single smallest values; instead, you want to look at a certain % or # of cases with the largest and smallest values. There are several ways to do this. The simplest, but most limited way, is to choose: o Analyze, then Descriptive Statistics, then either descriptives or explore. Click statistics in the explore dialog box and select outliers in the explore statistics dialog box. You will receive a list of cases with the 5 smallest and the 5 largest values for a particular variable. Values that are defined as missing aren’t included, so if you see missing values in the list, there’s something wrong. Check the other values if they appear to be unusual. [see Table e]
Table e [using the Explore command]
Extreme Values
Case Number Value Hours Per Day Highest 1 1402 24 Watching TV 2 466 22 3 300 20 4 1360 20 5 115 16a Lowest 1 1500 0 2 1400 0 3 1373 0 4 1372 0 5 1356 0b a. Only a partial list of cases with the value 16 are shown in the table of upper extremes. b. Only a partial list of cases with the value 0 are shown in the table of lower extremes. You can see that one of the respondents claims to watch television 24 hours a day. You know that’s not correct. It’s possible that he or she understood the question to mean how many hours is the TV set on. When analyzing the TV variable, you’ll have to decide what to do with people who have reported impossible values. In Table e, you see that there are only 4 cases with values of 16 hours or greater and then there is a gap until 12 hours. You might want to set values greater than 12 hours to 12 hours when analyzing the data. This is similar to what many people do when dealing with a variable for “age.”
Is there anything strange about the distribution of values? The next task is to examine the distribution of the values using histograms or stem-and-leaf plots. Make a stem-and-leaf plot [for small data sets] or a histogram of the data using either Graphs/Histogram or the Explore Plots dialog box. You want to look for unusual patterns in your data. For example, look at the histogram of ages in Table f. Ask yourself where all of the 30-year-olds have gone? Why are there no people above the age of 90? Were there really no people younger than 18 in the survey?
Looking At the Distribution of Values Are there logical impossibilities? For example, if you have a data file of hospital admissions, you can make a frequency table to count the reason for admission and the number of male and female admissions. Looking at these tables, you may not notice anything strange. However, if you look at these 2 variables together in a Crosstabs table, you may uncover unusual events. For instance, you may find males giving birth to babies, and women undergoing prostate surgery. Sometimes, pairs of variables have values that must be ordered in a particular way. For example, if you ask a woman her current age, her age at first marriage, and the duration of her first marriage, you know that the current age must be greater than or equal to the age at first marriage. You also know that the age at first marriage plus the duration of first marriage cannot exceed the current age. Start by looking at the simplest relationship: Is the age at first marriage less than the current age? You can plot the two variables on a scatterplot and look for cases that have unacceptable values. You know that all of the points must fall on or above the identity line.
TIP 10 For large data files, the drawback to this approach is that it’s tedious and prone to error. A better way is to create a new variable that is the difference between the current age and the age at first marriage. Then use data, select cases to select cases with negative values and analyze, then reports, then case summaries to list the pertinent information. Once you’ve remedied the age problem, you can create a new variable that is the sum of the age at first marriage and the duration of first marriage. You can then find the difference between this sum and the current age. Reset the select cases criteria and use case summaries to list cases with offending values.
Is there consistency? For a survey, you often have questions that are conditional. For example, first you ask Do you have a car? and then, if the answer is Yes, you ask insightful questions about the car. You can make Crosstabs tables of the responses to the main question with those to the subquestions. You have to decide how to deal with these inconsistencies: do you impute answers to the main question, or do you discard answers to subquestions? It’s your call.
Is there agreement? This refers to whether you have pairs of variables that convey similar information in different ways. For example, you may have recorded both years of education and highest degree earned. Or, you may have created a new variable that groups age into 2 categories, such as less than 25, 25 to 50, and older than 50. Compare the values of the 2 variables using crosstabs. The table may be large, but it’s easy to check the correspondence between the 2 variables. You can also identify problems by plotting the values of the 2 variables.
Are there unusual combinations of values? Identify any outliers so that you can make sure the values of these variables are correct and make any necessary adjustments. What counts as an outlier depends on the variables that are being considered together.
TIP 11 You can identify points in a scatterplot by specifying a variable in the Label Cases By text box in the Scatterplot dialog box. Double-click the plot to activate it in the Chart Editor. From the Elements menu, choose Data Label Mode or click on the Data Label Mode icon on the toolbar. This changes your cursor to a black box. Click the cursor over the point that you want identified by the value of the labeling variable. To go to that case in the Data Editor, right click on the point, and then left click. Make sure that the Data Editor is in Data View. To turn Data Label Mode off, click on the Data label Mode icon on the toolbar.
Transforming Your Data Before you transform your data, be sure that you know that value of the variables that you are interested in so that you know how to code the information. See earlier instructions about how to use the utilities menu to obtain information on the variables either individually or for the entire working data file.
Computing a New Variable If you want to perform the same calculation for all of the cases in your data file, the transformation is called unconditional. If you want to perform different computations based on the values of 1 or more variables, the transformation is conditional. For example, if you compute an index differently for men and women, the transformation is conditional. Both types of transformations can be performed in the Compute Variable dialog box.
One Size Fits All: Unconditional Transformation Choose compute from the transform menu to open the compute variable dialog box. At the top left, assign a new name to the variable that you will be computing. To do so, click in the target variable box and type in the desired name. You must follow the same rules for assigning variable names as you did when naming variables in the Data Editor. Also, don’t forget to enter the information in the type and label tab in the dialog box.
Warning: You MUST use a new variable name rather than one already in use. If you reuse the same name and make a mistake specifying the transformation, you’ll replace the values of the original variable with values that you don’t want. If you don’t catch the mistake right away, and you save the data file, the original values of the variable are lost. SPSS will ask you for permission to proceed if you try to use an existing variable name. To specify the formula for the calculations that you want to perform, either type directly in the Numeric Expression text box or use the calculator pad. Each time you want to refer to an existing variable, click it in the variable list and then click the arrow button. The variable name will appear in the formula at the blinking insertion point. Once you click ok, the variable is added to your data file as the last variable. However, remember that you want to click the paste button and then run the syntax command from the syntax window so that you know what commands you specified. You also want to remember to use commentary information above the pasted syntax in order to tell yourself and the reviewer, in this case me, what you did to conduct your analysis.
TIP 12 Right-click your mouse on any button (except the #s) on the calculator pad or any function for an explanation of what it means.
Using a Built-in Function The function groups are located in the dialog box and can be used to perform your calculations, if necessary. There are 7 main groups of functions: arithmetic, statistical, string, data and time, distribution, random-variable, and missing-values. If you wish to use it, click it when the blinking insertion point is placed where you want to insert the function into your formula, and then click the up arrow button. The function will appear in your formula, but it will have question marks for the arguments. The arguments of a function are the numbers or strings that it operates on. In the expression SQRT(25), 25 is the sole argument of this function. Enter a value for the argument, or double-click a variable to move it into the argument list. If there are more question- mark arguments, select them in turn and enter a value, move a variable, or somehow supply whatever suits the needs of the function.
TIP 12 For detailed information about any function and its arguments, from the Help menu, choose Topics, click the index tab, and type the word functions. You can then select the type of function that you want.
If and Then: Conditional Transformation If you want to use different formulas, depending on the values of one or more existing variables, you have to enter the formula and then click the button labeled if at the bottom of the compute variable dialog box. This will take you a secondary compute data dialog box in which you choose, “include if cases satisfies condition.” To make your conditional equation. For example, if you wish to compute a new variable, you would specify how the new target variable is coded in reference to the “if, then expression.”
Changing the Coding Scheme Recode into Same Variables If you wish to change the coding of a variable but not create a totally different variable, you would select transform, recode, into same variables, and click on the variable or variables of interest and move them into the variable box by clicking the arrow. Depending on how you wish to recode the values within a variable, you could select old and new values and on the left side of the dialog box, choose the numbers that you wish to change and on the right side of the dialog box, choose what you want them to become and click add. When done, select continue, to go back to the previous dialog box and paste command syntax so that you can run it. Again don’t forget to type in a commentary of what the command is doing. In other cases, you might choose the “IF” tab to compute the conditions under which a recode will take place.
TIP 13 If you wish to recode a group of variables using the same coding scheme, such as recode a 2 into a 1 for a set of variables even if the numbers stand for different value labels, you can enter several variables into the dialog box at once.
Recode into Different Variables If you want to recode an existing variable into a new one in which every original value has to be transformed into a value of the new variable. Click transform, recode, into different variables and you will get a dialog box. In this dialog box, select the name of the variable that will be recoded. Then in the output variable name test box, enter a name for the new variable. Click the change button and the new name appears after the arrow in the central list. Once this is done, click “old and new values” and enter the recode criteria that will comprise the command syntax. SPSS carries out the recode specifications in the order they are listed in the old to new list.
TIP 14 Always specify all of the values even if you’re leaving them unchanged. Select all other values and then copy cold values. Remember to click the add button after entering each specification to move it into the old to new list; otherwise, it is ignored.
Checking the Recode The easiest method is to make a crosstabs table of the original variable with the new variable containing recoded values.
Warning: After you’ve created a new variable with recode, go to the variable view in the Data Editor and set the missing values for each newly created variable.
Describing Your Data Examining Tables and Chart Counts Frequency Tables Rap Music
Cumulative Frequency Percent Valid Percent Percent Valid Like Very Much 41 2.7 2.9 2.9 Like It 145 9.7 10.1 13.0 Mixed Feelings 266 17.7 18.6 31.6 Dislike It 401 26.7 28.0 59.6 Dislike Very Much 578 38.5 40.4 100.0 Total 1431 95.4 100.0 Missing DK Much About It 58 3.9 NA 11 .7 Total 69 4.6 Total 1500 100.0
Imagine that you were interested in analyzing respondents views regarding rap music. You would run a frequency table like the one above to find a count of the level of like or dislike of rap music reported by respondents. Each row of the table corresponds to one of the recorded answers. Be sure to make sure that the counts presented appear to be correct, including those for the missing data listing.
The 3rd-5th columns contain percentages. The 3rd column labeled simply percent is the % of all cases in the data file with that value. 9% of respondents reported that they like rap music. However, the 4th column, labeled valid percent indicates that 10% of respondents like rap music. Why the difference? The 4th column bases the % only on people who actually respondent to the question.
Warning: A large difference between the % and valid % columns can signal big problems for your study. If the missing values result from people not being asked the question because that’s the design of the study, you don’t have to worry. If people weren’t asked because the interviewer decided not to ask them or if they refused to answer, that’s a different matter.
The 5th column, labeled cumulative percent is the sum of the valid % for that row and all of the rows before it. It’s useful only if the variable is measured at least on an ordinal scale. For example, the cumulative % for “like” tells you that 13% of respondents either reported that they like rap music or that they like it very much. The valid data value that occurs most frequently is called the mode. For these data, “dislike very much” is the modal category since 578 of the respondents reported that they disliked rap music very much. The mode is not a particularly good summary measure, and if you report it, you should always indicate the percentage of cases with that value. For variables measured on a nominal scale, the mode is the only summary statistic that makes sense, but that isn’t the case for this variable because there is a natural order to the responses [i.e. ordinal variable]. Frequency Tables as Charts You can display the numbers in a frequency table in a pie chart or a bar chart, although prominent statisticians advise that one should “never use a pie chart.” Rap Music Like Very Much Like It Mixed Feelings Dislike It 2.87% Dislike Very Much 10.13%
40.39% 18.59%
28.02%
__ Warning: If you create a pie chart by choosing Descriptive Statistics, then frequencies, a slice for missing values is always included. Use graph, then select pie if you don’t want to include a slice for missing values. This was the way that I obtained the pie chart above. 50.0%
40.0%
30.0% t n e c r e P
20.0%
10.0%
0.0% Like Very Much Like It Mixed Feelings Dislike It Dislike Very Much Rap Music
Examining Tables and Chart Counts Now you know how people as a group feel about rap music, but what about more nuanced information about the kinds of people who hold these views. Are they male? College Educated? Racial and Ethnic Minorities? To find out this information, you need to look at attitudes regarding rap music in conjunction with other variables. A crosstabualtion involving a 2-way table of counts, for attitudes toward rap music and gender. Gender is the row variable since it defines the rows of the table, and attitudes toward rap music is the column variable since it defines the columns. Each of the unique combinations of the values of the 2 variables defines a cell of the table. The numbers in the total row and column are called marginals because they are in the margins of the table. They are frequency tables for the individual variables.
TIP 15 DON’T be alarmed if the marginals in the crosstabulation aren’t identical to the frequency tables for the individual variables. Only cases with valid values for both variables are in the crosstabulation, so if you have cases with missing values for one variable but not the other, they will be excluded from the crosstabulation. Respondents who tell you their gender but not their attitudes about rap music are included in the frequency table for gender but not in the crosstabulation of the 2 variables. The table below shows a crosstabulation that contains information solely on the number of cases that meet both criteria, but not a % distribution.
Respondent's Sex * Rap Music Crosstabulation
Count Rap Music Like Very Mixed Dislike Much Like It Feelings Dislike It Very Much Total Respondent's Male 17 62 97 181 258 615 Sex Female 24 83 169 220 320 816 Total 41 145 266 401 578 1431
Percentages The above information, i.e. the counts in the cell are the basic elements of the table, but they are usually not the best choice for reporting findings because they cannot be easily compared if there are different totals in the rows and columns of the table. For example, if you know that 17 Males and 24 Females like rap music very much, you can conclude little about the relationship between the 2 variables unless you also know the total of men and women in the sample.
For a crosstabulation, you can compute 3 different percentages: Row %: the cell count divided by the number of cases in the row times 100 Column %: the cell count divided by the number of cases in the column times 100 Total %: the cell count divided by the total number of cases in the table times 100
The 3 % convey different information, so be sure to choose the correct one for your problem. If one of the 2 variables in your table can be considered an independent variable and the other a dependent variable, make sure the % sum up to 100 for each category of the independent variable. Respondent's Sex * Rap Music Crosstabulation
Rap Music Like Very Mixed Dislike Much Like It Feelings Dislike It Very Much Total Respondent's Male Count 17 62 97 181 258 615 Sex % within 2.8% 10.1% 15.8% 29.4% 42.0% 100.0% Respondent's Sex % within Rap Music 41.5% 42.8% 36.5% 45.1% 44.6% 43.0% % of Total 1.2% 4.3% 6.8% 12.6% 18.0% 43.0% Female Count 24 83 169 220 320 816 % within 2.9% 10.2% 20.7% 27.0% 39.2% 100.0% Respondent's Sex % within Rap Music 58.5% 57.2% 63.5% 54.9% 55.4% 57.0% % of Total 1.7% 5.8% 11.8% 15.4% 22.4% 57.0% Total Count 41 145 266 401 578 1431 % within 2.9% 10.1% 18.6% 28.0% 40.4% 100.0% Respondent's Sex % within Rap Music 100.0% 100.0% 100.0% 100.0% 100.0% 100.0% % of Total 2.9% 10.1% 18.6% 28.0% 40.4% 100.0%
Since gender would fall under the realm of an independent variable, you want to calculate the row % because they will tell you what % of women and men fall into each of the attitudinal categories. This % isn’t affected by unequal numbers of males and females in your sample. From the row % displayed above, you find that 2.8% of males like rap music very much as do 2.9% of females. So with regard to strong positive feelings about rap music, you note that there are no visible differences. Note: No statistical differences are examined yet. From the column% displayed above, you find that among those who like rap music very much, 41.5% are men and 58.5% are female. This does not tell you that females are significantly more likely to report liking rap music very much than males. Instead, it tells you that of the people who like rap music very much, women tend to hold a stronger view than men. Note: The column % depend on the number of men and women in the sample as well as how they feel about rap music. If men and women have identical attitudes but there are twice as many men in the survey than women, the column % for men will be twice as large as the column % for women. You can’t draw any conclusions based on only the column %.
TIP 16 If you use row %, compare the % within a column. If you use column %, compare the % within a row.
Multiway Tables of Counts as Charts You can plot the % in the table above by using a clustered bar chart like the one below. For each attitudinal category regarding rap music, there are separate bars for men and women since gender is the cluster variable. The values plotted are the % of all men and the % of all women who gave each response. You can easily that females are equally likely to like rap music very much as much as males. Although the same information is in the crosstabulation, it is easier to see in the bar chart.
50.0% Respondent's Sex Male Female
40.0%
30.0% t n e c r e P
41.95% 20.0% 39.22%
29.43% 26.96%
10.0% 20.71% 15.77%
10.08%10.17%
2.76% 2.94% 0.0% Like Very Like It Mixed Dislike It Dislike Very Much Feelings Much Rap Music
TIP 17 Always select % in the clustered bar chart dialog boxes; otherwise, you’ll have a difficult time making comparisons within a cluster, since the height of the bars will depend on the number of cases in each subgroup. For example, you won’t be able to tell if the bar for men who always read newspapers is higher because men are more likely to read a newspaper daily or because there are more men in the sample.
Control Variables You can examine the relationship between gender and attitudes toward rap music separately for each category of another variable, such as education [i.e., the control variable]. See the crosstabulation model below to show you how the information would look when entered into the crosstabulation dialog box.
Respondent's Sex * Rap Music * RS Highest Degree Crosstabulation
Rap Music Like Very Mixed Dislike RS Highest Degree Much Like It Feelings Dislike It Very Much Total Less than HS Respondent's Male Count 5 11 14 30 55 115 Sex % within 4.3% 9.6% 12.2% 26.1% 47.8% 100.0% Respondent's Sex Female Count 10 18 19 35 59 141 % within 7.1% 12.8% 13.5% 24.8% 41.8% 100.0% Respondent's Sex Total Count 15 29 33 65 114 256 % within 5.9% 11.3% 12.9% 25.4% 44.5% 100.0% Respondent's Sex High school Respondent's Male Count 9 36 50 87 110 292 Sex % within 3.1% 12.3% 17.1% 29.8% 37.7% 100.0% Respondent's Sex Female Count 11 45 95 134 175 460 % within 2.4% 9.8% 20.7% 29.1% 38.0% 100.0% Respondent's Sex Total Count 20 81 145 221 285 752 % within 2.7% 10.8% 19.3% 29.4% 37.9% 100.0% Respondent's Sex Junior college Respondent's Male Count 1 4 4 13 14 36 Sex % within 2.8% 11.1% 11.1% 36.1% 38.9% 100.0% Respondent's Sex Female Count 1 3 13 15 18 50 % within 2.0% 6.0% 26.0% 30.0% 36.0% 100.0% Respondent's Sex Total Count 2 7 17 28 32 86 % within 2.3% 8.1% 19.8% 32.6% 37.2% 100.0% Respondent's Sex Bachelor Respondent's Male Count 2 8 22 32 41 105 Sex % within 1.9% 7.6% 21.0% 30.5% 39.0% 100.0% Respondent's Sex Female Count 2 11 30 27 52 122 % within 1.6% 9.0% 24.6% 22.1% 42.6% 100.0% Respondent's Sex Total Count 4 19 52 59 93 227 % within 1.8% 8.4% 22.9% 26.0% 41.0% 100.0% Respondent's Sex Graduate Respondent's Male Count 3 7 19 38 67 Sex % within 4.5% 10.4% 28.4% 56.7% 100.0% Respondent's Sex Female Count 5 12 9 16 42 % within 11.9% 28.6% 21.4% 38.1% 100.0% Respondent's Sex Total Count 8 19 28 54 109 % within 7.3% 17.4% 25.7% 49.5% 100.0% Respondent's Sex
You see that the largest difference in strong dislike of rap music between men and women occurs among those with a graduate degree. 56.7% of males strongly dislike rap compared to 38.1% of females. The % are almost equal for those with a high school education.
As the number of variables in a crosstabulation increases, it becomes unwieldy to plot all of the categories of a variable. Instead you can restrict your attention to a particular responses.
T-Tests When using these statistical tests, you are testing the null hypothesis that 2 population means are equal. The alternative hypothesis is that they are not equal. There are 3 different ways to go about this, depending on how the data were obtained.
Deciding Which T-test to Use Neither the one-sample t test nor the paired samples t test requires any assumption about the population variances, but the 2-sample t test does.
TIP 18 When reporting the results of a t test, make sure to include the actual means, differences, and standard errors. Don’t give just a t value and the observed significance level.
One-sample T test If you have a single sample of data and want to know whether it might be from a population with a known mean, you have what’s termed a one-sample design, which can be analyzed with a one-sample t test.
Examples You want to know whether CEOs have the same average score on a personality inventory as the population on which it was normed. You administer the test to a random sample of CEOs. The population value is assumed to be known in advance. You don’t estimate it from your data. You’re suspicious of the claim that the normal body temperature is 98.6 degrees. You want to test the null hypothesis that the average body temperature for human adults is the long assumed value of 98.6, against the alternative hypothesis that it is not. The value 98,6 isn’t estimated from the data; it is a known constant. You take a single random sample of 1,000 adult men and women and obtain their temperatures. You think that 40 hours no longer defines the traditional work week. You want to test the null hypothesis that the average work week is 40 hours, against the alternative that it isn’t. You ask a random sample of 500 full-time employees how many hours they worked last week. You want to know whether the average IQ score for children diagnosed with schizophrenia differs from 100, the average for the population of all children. You administer an IQ test to a random sample of 700 schizophrenic children. Your null hypothesis is that the population value for the average IQ score for schizophrenic children is 100, and the alternative hypothesis is that it isn’t. Data Arrangement For the one-sample t test, you have one variable that contains the values for each case. For example: A manufacturer of high-performance automobiles produces disc brakes that must measure 322 millimeters in diameter. Quality control randomly draws 16 discs made by each of eight production machines and measures their diameters. This example uses the file brakes.sav . Use One Sample T Test to determine whether or not the mean diameters of the brakes in each sample significantly differ from 322 millimeters. A nominal variable, Machine Number, identifies the production machine used to make the disc brake. Because the data from each machine must be tested as a separate sample, the file must first be split into groups by Machine Number. Select compare groups in the split file dialog box. Select machine number from the variable listing and move it into the box for “groups based on.” Select the “compare groups circle” and since the file isn’t already sorted, be sure that you have selected, “sort the file by grouping variables.”
Next select one-sample T test from the analyze tab.
Select analyze, then compare means, and then one-sample T test. Select the test variable, i.e. disc brake diameter (mm), type 322 as the test variables, and click options.
In the options dialog box for the one-sample T test, type 90 in the confidence interval %, then be sure that you have missing values coded as “exclude cases analysis by analysis,” then click continue, then click paste so that the syntax is entered in the syntax viewer, and then select ok. Note: A 95% confidence interval is generally used, but the examples below reflect a 90% confidence interval.
The Descriptives table displays the sample size, mean, standard deviation, and standard error for each of the eight samples. The sample means disperse around the 322mm standard by what appears to be a small amount of variation. The test statistic table shows the results of the one-sample T test.
The t column displays the observed t statistic for each sample, calculated as the ratio of the mean difference divided by the standard error of the sample mean.
The df column displays degrees of freedom. In this case, this equals the number of cases in each group minus 1.
The column labeled Sig. (2-tailed) displays a probability from the t distribution with 15 degrees of freedom. The value listed is the probability of obtaining an absolute value greater than or equal to the observed t statistic, if the difference between the sample mean and the test value is purely random.
The Mean Difference is obtained by subtracting the test value (322 in this example) from each sample mean.
The 90% Confidence Interval of the Difference provides an estimate of the boundaries between which the true mean difference lies in 90% of all possible random samples of 16 disc brakes produced by this machine.
Since their confidence intervals lie entirely above 0.0, you can safely say that machines 2, 5 and 7 are producing discs that are significantly wider than 322mm on the average.
Similarly, because its confidence interval lies entirely below 0.0, machine 4 is producing discs that are not wide enough. The one-sample t test can be used whenever sample means must be compared to a known test value. As with all t tests, the one-sample t test assumes that the data be reasonably normally distributed, especially with respect to skewness. Extreme or outlying values should be carefully checked; boxplots are very handy for this.
Paired-Samples T test You use a paired-samples (also known as the matched cases) T test if you want to test whether 2 population means are equal, and you have 2 measurements from pairs of people or objects that are similar in some important way. For example, you’ve observed the same person before and after treatment or you have personally measures for each CEO and their non-CEO sibling. Each “case” in this data file represents a pair of observations.
Examples You are interested in determining whether self-reported weights and actual weights differ. You ask a random sample of 200 people how much they weigh and then you weigh them on a scale. You want to compare the means of the 2 related sets of weights. You want to test the null hypothesis that husbands and wives have the same average years of education. You take a random sample of married couples and compare their average years of education. You want to compare 2 methods for teaching reading. You take a random sample of 50 pairs of twins and assign each member of a pair to one of the 2 methods. You compare average reading scores after completion of the program.
Data Arrangement In a paired-samples design, both members of a pair must be on the same data record. Different variable names are used to distinguish the 2 members of a pair. For example: A physician is evaluating a new diet for her patients with a family history of heart disease. To test the effectiveness of this diet, 16 patients are placed on the diet for 6 months. Their weights and triglyceride levels are measured before and after the study, and the physician wants to know if either set of measurements has changed. This example uses the file dietstudy.sav . Use Paired-Samples T Test to determine whether there is a statistically significant difference between the pre- and post- diet weights and triglyceride levels of these patients.
o Select Analyze, then compare means, then paired-samples T test Select Triglyceride and Final Triglyceride as the first set of paired variables.
Select Weight and final weight as the second pair and click ok. The Descriptives table displays the mean, sample size, standard deviation, and standard error for both groups. The information is disseminated in pairs such that pair 1 should come first and pair 2 should come second in the table.
Across all 16 subjects, triglyceride levels dropped between 14 and 15 points on average after 6 months of the new diet.
The subjects clearly lost weight over the course of the study; on average, about 8 pounds.
The standard deviations for pre- and post-diet measurements reveal that subjects were more variable with respect to weight than to triglyceride levels.
At -0.286, the correlation between the baseline and six-month triglyceride levels is not statistically significant. Levels were lower overall, but the change was inconsistent across subjects. Several lowered their levels, but several others either did not change or increased their levels.
On the other hand, the Pearson correlation between the baseline and six-month weight measurements is 0.996, almost a perfect correlation. Unlike the triglyceride levels, all subjects lost weight and did so quite consistently. The Mean column in the paired-samples t test table displays the average difference between triglyceride and weight measurements before the diet and six months into the diet.
The Std. Deviation column displays the standard deviation of the average difference score.
The Std. Error Mean column provides an index of the variability one can expect in repeated random samples of 16 patients similar to the ones in this study.
The 95% Confidence Interval of the Difference provides an estimate of the boundaries between which the true mean difference lies in 95% of all possible random samples of 16 patients similar to the ones participating in this study.
The t statistic is obtained by dividing the mean difference by its standard error.
The Sig. (2-tailed) column displays the probability of obtaining a t statistic whose absolute value is equal to or greater than the obtained t statistic.
Since the significance value for change in weight is less than 0.05, you can conclude that the average loss of 8.06 pounds per patient is not due to chance variation, and can be attributed to the diet.
However, the significance value greater than 0.10 for change in triglyceride level shows the diet did not significantly reduce their triglyceride levels.
Warning: When you click the first variable of a pair, it doesn’t move to the list box; instead, it moves to the lower left box labeled Current Selections. Only when you click a second variable and move it into Current Selections can you move the pair into the Paired Variable list. Two-Independent-Samples T test If you have 2 independent groups of subjects, such as CEOs and non-CEOs, men and women, or people who received a treatment and people who didn’t, and you want to test whether they come from populations with the same mean for the variable of interest, you have a 2-independent samples design. In an independent-samples design, there is no relationship between people or objects in the 2 groups. The T test you use is called an independent-samples T test.
Examples You want to test the null hypothesis that, in the U.S. population, the average hours spent watching TV per day is the same for males and females. You want to compare 2 teaching methods. One group of students is taught by one method, while the other group is taught by the other method. At the end of the course, you want to test the null hypothesis that the population values for the average scores are equal. You want to test the null hypothesis that people who report their incomes in a survey have the same average years of education as people who refuse.
Data Arrangement If you have 2 independent groups of subjects, e.g., boys and girls, and want to compare their scores, your data file must contain two variables for each child: one that identifies whether a case is a boy or a girl, and one with the score. The same variable name is used for the scores for all cases. To run the 2 independent samples T test, you have to tell SPSS which variable defines the groups. That’s the variable Gender, which is moved into the Grouping Variable box. Notice the 2 question marks after a variable name. They will disappear after you use the Define Groups dialog box to tell SPSS which values of the variable should be used to form the 2 groups.
TIP 18 Right-click the variable name in the Grouping Variable box and select variable information from the pop-up menu. Now you can check the codes and value labels that you’ve defined for that variable.
Warning: In the define groups dialog box, you must enter the actual values that you entered into the data editor, not the value labels. If you used the codes of 1 for male and 2 for female and assigned them value labels of m and f, then you enter the values 1 and 2, not the labels m and f, into the define groups dialog box.
An analyst at a department store wants to evaluate a recent credit card promotion. To this end, 500 cardholders were randomly selected. Half received an ad promoting a reduced interest rate on purchases made over the next three months, and half received a standard seasonal ad.
Select Analyze, then compare means, then independent samples T test Select money spent during the promotional period as the test variable. Select type of mail insert received as the grouping variable. Then click define groups.
Type 0 as the group 1 variable and 1 as the group 2 variable under define groups. For the default, the program should have “use specified values” selected. Then click continue and ok. The Descriptives table displays the sample size, mean, standard deviation, and standard error for both groups. On average, customers who received the interest-rate promotion charged about $70 more than the comparison group, and they vary a little more around their average.
The procedure produces two tests of the difference between the two groups. One test assumes that the variances of the two groups are equal. The Levene statistic tests this assumption.
In this example, the significance value of the statistic is 0.276. Because this value is greater than 0.10, you can assume that the groups have equal variances and ignore the second test. Using the pivoting trays, you can change the default layout of the table so that only the "equal variances" test is displayed.
Activate the pivot table. Then under pivot, select pivoting trays. Drag assumptions from the row to the layer and close the pivoting trays window.
With the test table pivoted so that assumptions are in the layer, the Equal variances assumed panel is displayed.
The df column displays degrees of freedom. For the independent samples t test, this equals the total number of cases in both samples minus 2. The column labeled Sig. (2-tailed) displays a probability from the t distribution with 498 degrees of freedom. The value listed is the probability of obtaining an absolute value greater than or equal to the observed t statistic, if the difference between the sample means is purely random.
The Mean Difference is obtained by subtracting the sample mean for group 2 (the New Promotion group) from the sample mean for group 1.
The 95% Confidence Interval of the Difference provides an estimate of the boundaries between which the true mean difference lies in 95% of all possible random samples of 500 cardholders.
Since the significance value of the test is less than 0.05, you can safely conclude that the average of 71.11 dollars more spent by cardholders receiving the reduced interest rate is not due to chance alone. The store will now consider extending the offer to all credit customers.
Churn propensity scores are applied to accounts at a cellular phone company. Ranging from 0 to 100, an account scoring 50 or above may be looking to change providers. A manager with 50 customers above the threshold randomly samples 200 below it, wanting to compare them on average minutes used per month.
Select analyze, then compare means, then independent samples T test Select average monthly minutes as the test variable and propensity to leave as the group variable. Then select define groups. Select cut point and type 50 as the cut point value. Then click continue and ok.
The Descriptives table shows that customers with propensity scores of 50 or more are using their cell phones about 78 minutes more per month on the average than customers with scores below 50.
The significance value of the Levene statistic is greater than 0.10, so you can assume that the groups have equal variances and ignore the second test. Using the pivoting trays, change the default layout of the table so that only the "equal variances" test is displayed. Play around with the pivot tray link if you wish. The t statistic provides strong evidence of a difference in monthly minutes between accounts more and less likely to change cellular providers.
Analyzing Truancy Data: The Example
To perform this analysis in order to test your skills using a T test, please see the spss file on the course blackboard page.
One-Sample T test
Consider whether the observed truancy rate before intervention [the % of school days missed because of truancy] differs from an assumed nationwide truancy rate of 8%. You have one sample of data [students enrolled in the TRP program-truancy reduction program] and you want to compare the results to a fixed, specified in-advance population value.
The null hypothesis is that the sample comes from a population with an average truancy rate of 8%. [Another way of stating the null hypothesis is that the difference in the population means between your population and the nation as a whole is 0.] The alternative hypothesis is that you sample doesn’t come from a population with a truancy rate of 8%.
To obtain the table below, you would do one of the following: Go to Analyze, choose desciptive statistics, then descriptives, select the variable to be examined, in this case prepct, then go to options in the descriptives dialog box and select, mean, minimu, maximum, and standard deviation, then select continue and okay. You can also choose frequencies under the descriptive statistics link, select the variable to be examined, go to statistics and pick the same statistics as above, select continue, and then okay. Descriptive Statistics
N Minimum Maximum Mean Std. Deviation prepct Percent truant 299 .00 72.08 14.2038 13.07160 days pre intervention Valid N (listwise) 299
From the table above, you see that, for the 299 students in this sample, the average truancy rate is 14.2%. You know that even if the sample is selected from a population in which the true rate is 8%, you don’t expect your sample to have an observed rate of exactly 8%. Samples from the population vary. What you want to determine is whether it’s plausible for a sample of 299 students to have an observed truancy rate of 14.2% if the population value is 8%.
TIP 19 Before you embark on actually computing a one-sample T test, make certain checks. Look at the histogram of the truancy rates to make sure that all of the values make sense. Are there percentages smaller than 0 or greater than 100? Are there values that are really far from the rest? If so, make sure they’re not the result of errors. If you have a small number of cases, outliers can have a large effect on the mean and the standard deviation.
Checking the Assumptions To use the one-sample T test, you have to make certain assumptions about the data: The observations must be independent of each other. In this data file, students came from 17 schools, so its possible that students in the same school may be more similar than students in different schools. If that’s the case, the estimated significance level may be smaller than it should be, since you don’t have as much information as the sample size indicates. [If you have 10 students from 10 different schools, that’s more information than having 10 students from the same school because it’s plausible that students in the same school are more similar than students from different schools.] Independence is one of the most important assumptions that you have to make when analyzing data. In the population, the distribution of the variable must be normal, or the sample size must be large enough so that it doesn’t matter. The assumption of normally distributed data is required for many statistical tests. The importance of the assumption differs, depending on the statistical test. In the case of a one-sample T test, the following guidelines are suggested: If the number of cases is < 15, the data should be approximately normally distributed; if the number of cases is between 15 and 40, the data should not have outliers or be very skewed; for samples of 40 or more, even markedly skewed distributions are acceptable. Because you have close to 300 observations, there’s little need to worry about the assumption of normality.
TIP 20 If you have reason to believe that the assumptions required for the T test are violated in an important way, you can analyze the data using a nonparametric tests.
Testing the Hypothesis Compute the difference between the observed sample mean and the hypothesized population value. [14.2%-8% = 6.2%]
Compute the standard error of the difference. This is a measure of how much you expect sample means, based on the same number of cases from the same population, to vary. The hypothetical population value is a constant and doesn’t contribute to the variability of the differences, so the standard error of the difference is just the standard error of the mean. Based on the standard deviation in the table above, the standard error equals: SE = std. deviation/SQRT of the sample size = 13.07/SQRT of 299 = .756 [Note: You should be able to obtain this value using the frequencies command and selecting standard error mean under statistics. This is a way for you to double check if you are unsure of your calculations. See the table below.
Statistics
prepct Percent truant days pre intervention N Valid 299 Missing 0 Mean 14.2038 Std. Error of Mean .75595 Std. Deviation 13.07160
You can calculate the t statistic by hand if you divide the observed difference by the standard error of the difference. T = Observed Mean [prepct]-Predicted Mean/Std. Error of the mean = 14.204-8/0.756 = 8.21
You can also conduct a one-sample T test using SPSS by going to analyze, compare means, one-sample T test, selecting the relevant variable, [i.e. prepct] and entering it into the test variable box and entering the number 8 in the test value box at the bottom of the dialog box and running the analysis. You will get the following output as shown below.
T-TEST /TESTVAL = 8 /MISSING = ANALYSIS /VARIABLES = prepct /CRITERIA = CI(.95) . T-Test One-Sample Statistics
Std. Error N Mean Std. Deviation Mean prepct Percent truant 299 14.2038 13.07160 .75595 days pre intervention
One-Sample Test
Test Value = 8 95% Confidence Interval of the Mean Difference t df Sig. (2-tailed) Difference Lower Upper prepct Percent truant 8.207 298 .000 6.20378 4.7161 7.6915 days pre intervention
Use the T distribution to determine if the observed t statistic is unlikely if the null hypothesis is true. To calculate the observed significance level for a T statistic, you have to take into account both how large the actual T value is and how many degrees of freedom it has. For a one-sample T test, the degress of freedom [dof] is one fewer than the number of cases. From the table above, you see that the observed significance level is < .0001. Your observed results are very unlikely if the true rate is 8%, so you reject the null hypothesis. Your sample probably comes from a population with a mean larger than 8%.
TIP 21 To obtain observed significance levels for an alternative hypothesis that specifies direction, often known as a one-sided or one-tailed test, divide the observed two-tailed significance level by two. Be very cautious about using one-sided tests.
Examining the Confidence Interval If you look at the 95% Confidence Interval for the population difference, you see that it ranges from 4.7% to 7.7%. You don’t know whether the true population difference is in this particular interval, but you know that 95% of the time, 95% confidence intervals include the true population values. Note that the value of 0 is not included in the confidence interval. If your observed significance level had been larger than 0.05, 0 would have been included in the 95% confidence interval.
TIP 22 There is a close relationship between hypothesis testing and confidence intervals. You can reject the null hypothesis that you sample comes from a population with any value outside of the 95% confidence interval. The observed significance level for the hypothesis test will be less than 0.05.
Paired-Samples T test You’ve seen that your students have a higher truancy rate than the country as a whole. Now the question is whether there is a statistically significant difference in the truancy rates before and after the truancy reduction programs. For each student, you have 2 values for unexcused absences. One is for the year before the student enrolled in the program; the other is for the year in which the student was enrolled in the program. Since there are two measurements for each subject, a before and an after, you want to use a paired-samples T test to test the null hypothesis that averages before and after rates are equal in the population.
TIP 23 The reason for doing a paired-samples design is to make the 2 groups as comparable as possible on characteristics other than the one being studied. By studying the same students before and after intervention, you control for differences in gender, socioeconomic status, family supervision, and so on. Unless you have pairs of observations that are quite similar to each other, pairing has little effect and may, in fact, hurt your chances of rejecting the null hypothesis when it is false.
Before running the paired-samples T test procedure, look at the histogram of the differences shown. You should see that the shape of the distribution is symmetrical [i.e. not too far from normal]. Many of the cases cluster around 0, indicating that the difference in the before and after scores is small for these students.
Checking the Assumptions The same assumptions about the distributions of the data are required for this test as those in the one-sample T test. The observations should be independent; if the sample size is small, the distribution of differences should be approximately normal. Note that the assumptions are about the differences, not the original observations. That’s because a paired-samples T test is nothing more than a one-sample T test on the differences. If you calculate the differences between the pre- and post-values and use the one-sample T test with a population value of 0, you’ll get exactly the same statistic as using the paired- samples T test.
Testing the Hypothesis From the table below, you see that the average truancy rate before intervention is 14.2% and the average truancy rate after intervention is 11.4%. That’s a difference about 2.8%. To get the table below, you should go to descriptives and select the prepct and postpct variables and enter them into the variable list, be sure that the right statistics are checked off [e.g. standard deviation], and then hit okay. Paired Samples Statistics
Std. Error Mean N Std. Deviation Mean Pair postpct Percent truant 11.4378 299 11.18297 .64673 1 days post intervention prepct Percent truant 14.2038 299 13.07160 .75595 days pre intervention
To see how often you would expect to see a difference of at least 2.8% when the null hypothesis of no difference is true, look at the paired-samples T test table below.
To obtain the table below, do the following: go to analyze, then select compare means, then select paired-samples T test and choose the 2 variables of interest of the pair to be selected, i.e., prepct and postpct, then select Ok.
Paired Samples Test
Paired Differences 95% Confidence Interval of the Std. Error Difference Mean Std. Deviation Mean Lower Upper t df Sig. (2-tailed) Pair postpct Percent truant 1 days post intervention -2.76602 12.69355 .73409 -4.21067 -1.32137 -3.768 298 .000 - prepct Percent truant days pre intervention
The T statistic, 3.8, is computed by dividing the average difference [2.77%] by the standard error of the mean difference [0.73]. The degrees of freedom is the number of pairs minus one. The observed significance level is < .001, so you can reject the null hypothesis that the pre-intervention and post-intervention truancy rates are equal in the population. Intervention appears to have reduced the truancy rate.
Warning: The conclusions you can draw about the effectiveness of truancy reduction programs from a study like this are limited. Even if you restrict your conclusions to the schools from which these children are a sample, there are many problems. Since you are looking at differences in truancy rates between adjacent years, you aren’t controlling for possible increases or decreases in truancy that occur as children grow older. For example, if truancy increases with age, the effect of the truancy reduction program may be larger than it appears. There is also potential bias in the determination of what is considered an “excused” absence.
The 95% confidence interval for the population change is from 1.3% to 4.2%. It appears that if the program has an effect, it is not a very large one. One average, assuming a 180- day school year, students in the truancy reduction program attended school five more days after the program than before. The 95% confidence interval for the number of days “saved” is from 2.3 days to 7.6 days. A paired-samples design is effective only if you have pairs of similar cases. If your pairing does not result in a positive correlation coefficient between the 2 measurements of close to 0.5, you may lose power [your computer stays on, but your ability to reject the null hypothesis when it is false fizzles] by analyzing the data as a paired-samples design. From the correlation coefficient table covering the correlation coefficient between the pre- and post-intervention rates is close to 0.5, so pairing was probably effective. See below.
Paired Samples Correlations
N Correlation Sig. Pair postpct Percent truant 1 days post intervention 299 .461 .000 & prepct Percent truant days pre intervention
Warning: Although well-intentioned, paired designs often run into trouble. If you give a subject the same test before and after an intervention, the practice effect, instead of the intervention, may be responsible for any observed change. You must also make sure that there is no carryover effect; that is, the effect of one intervention must be completely gone before you impose another.
Two-Independent Samples T test
You’ve seen that intervention seems to have had a small, although statistically significant effect. One of the questions that remains is whether the effect is similar for boys and girls prior to intervention? Is the average truancy rate the same for boys and girls after intervention? Is the change in truancy rates before and after intervention the same for boys and girls?
Group Statistics
Std. Error gender Gender N Mean Std. Deviation Mean prepct Percent truant f Female 152 13.0998 12.25336 .99388 days pre intervention m Male 147 15.3453 13.81620 1.13954 postpct Percent truant f Female 152 11.5130 11.43948 .92786 days post intervention m Male 147 11.3599 10.94995 .90314
diffpct Pre - Post f Female 152 1.5866 11.72183 .95077 m Male 147 3.9850 13.55834 1.11827
The table above shows summary statistics for the 2 groups for all 3 variables. Boys had somewhat larger average truancy scores prior to intervention than did girls. The average scores after intervention were similar for the 2 groups. The difference between the average pre- and post-intervention is larger for boys. You must determine whether these observed differences are large enough for you to conclude that, in the population, boys and girls differ in average truancy rates. You can use the 2 independent-samples T test to test all 3 hypotheses.
Checking the Assumptions You must assume that all observations are independent. If the sample sizes in the groups are small, the data must come from populations that have normal distributions. If the sum of the sample sizes in the 2 groups is greater than 40, you don’t have to worry about the assumption of normality. The 2-independent-samples T test also requires assumptions about the variances in the 2 groups. If the 2 samples come from populations with the same variance, you should use the “pooled” or equal-variance T test. If the variances are markedly different, you should use the separate-variance T test. Both of these are shown below.
Independent Samples Test
Levene's Test for Equality of Variances t-test for Equality of Means 95% Confidence Interval of the Mean Std. Error Difference F Sig. t df Sig. (2-tailed) Difference Difference Lower Upper prepct Percent truant Equal variances 5.248 .023 -1.488 297 .138 -2.24550 1.50904 -5.21527 .72426 days pre intervention assumed Equal variances -1.485 290.226 .139 -2.24550 1.51207 -5.22151 .73051 not assumed postpct Percent truant Equal variances .122 .727 .118 297 .906 .15309 1.29578 -2.39698 2.70317 days post intervention assumed Equal variances .118 296.969 .906 .15309 1.29483 -2.39511 2.70130 not assumed diffpct Pre - Post Equal variances 1.679 .196 -1.638 297 .102 -2.39839 1.46426 -5.28003 .48326 assumed Equal variances -1.634 287.906 .103 -2.39839 1.46782 -5.28740 .49063 not assumed
You can test the null hypothesis that the population variances in the 2 groups are equal using the Levene test, shown above. If the observed significance level is small [in the column labeled sig. under Levene’s Test], you reject the null hypothesis that the population variances are equal. For this example, you can reject the null hypothesis that the per-intervention truancy variances are equal in the 2 groups. For the other 2 variables, you can’t reject the null hypothesis that the variances are equal.
Testing the Hypothesis
In the 2-independent-samples T test, the T statistic is computed the same as for the other 2 tests. It is the ratio of the difference between the 2 sample means divided by the standard error of the difference. The standard error of the difference is computed differently, depending on whether the 2 variances are assumed to be equal or not. That’s why you see 2 sets of T values in the table above. In this example, the 2 T values and confidence intervals based on them are very similar. That will always be the case when the sample size in the 2 groups is almost the same.
The degrees of freedom for the t statistic also depends on whether you assume that the 2 variances are equal. If the variances are assumed to be equal, the degrees of freedom is 2 fewer than the sum of the number of cases in the 2 groups. If you don’t assume that the variances are equal, the degrees of freedom is calculated from the actual variances and the sample sizes in the groups. The result is usually not an integer.
From the column labeled Sig. [2-tailed], you can’t reject any of the 3 hypotheses of interest. The observed results are not incompatible with the null hypothesis that boys and girls are equally truant before and after the program and that intervention affects confidence intervals.
Warning: When you compare 2 independent groups, one of which has a factor of interest and the other that doesn’t, you must be very careful about drawing conclusions. For example, if you compare people enrolled in a weight-loss program to people who aren’t, you cannot attribute observed differences to the program unless the people have been randomly assigned to two programs.
T-Tests
Crosstabulations
You classify cases based on values for 2 or more categorical variables [e.g. type of health insurance coverage and satisfaction with health care.] Each combination of values is called a cell. To test whether the two variables that make up the rows and columns are independent, you calculate how many cases you expect in each cell if the variables are independent, and compare these expected values to those actually observed using the chi- square statistic. If your observed results are unlikely if the null hypothesis of independence is true, you reject the null hypothesis. You can measure how strongly the row and column variables are related by computing measures of association. There are many different measures, and they define association in different ways. In selecting a measure of association, you should consider the scale on which the variables are measured, the type of association you want to detect, and the ease of interpretation of the measure. You can study the relationship between a dichotomous [2-category] risk factor and a dichotomous outcome [e.g. family history of a disease and development of the disease], controlling for other variables [e.g. gender] by computing special measures based on the odds.
Chi-Square Test: Are Two Variables Independent?
If you think that 2 variables are related, the null hypothesis that you want to test is that they are not related. Another way of stating the null hypothesis is that the 2 variables are independent. Independence has a very precise meaning in this situation. It means that the probability that a case falls into a particular cell of a table is the product of the probability that a case falls into that row and the probability that a case falls into that column.
Warning: The word independent as used here has nothing to do with dependent and independent variables. It refers to the absence of a relationship between 2 variables. As an example of testing whether 2 variables are independent, look at the table below, a crosstabulation of highest educational attainment [degree] and perception of life’s excitement[life] based on the gssdata posted on blackboard. From the row %, you see that the % of people who find life exciting is not exactly the same in the 5 degree groups, although it is fairly similar for the 1st 2 degree groups. Slightly less than half of those with less than a high school education or with a high school education find life exciting. However, you see that there is substantial differences between those with some exposure to college and those with a post-graduate degree. For those respondents, almost 2/3 find that life is exciting.
degree Highest degree * life Is life exciting, routine or dull? Crosstabulation
life Is life exciting, routine or dull? 1 Exciting 2 Routine 3 Dull Total degree 0 Lt high school Count 59 67 10 136 Highest Expected Count 70.8 60.2 5.0 136.0 degree % within degree 43.4% 49.3% 7.4% 100.0% Highest degree 1 High school Count 218 232 18 468 Expected Count 243.7 207.1 17.2 468.0 % within degree 46.6% 49.6% 3.8% 100.0% Highest degree 2 Junior college Count 41 23 2 66 Expected Count 34.4 29.2 2.4 66.0 % within degree 62.1% 34.8% 3.0% 100.0% Highest degree 3 Bachelor Count 94 46 3 143 Expected Count 74.4 63.3 5.3 143.0 % within degree 65.7% 32.2% 2.1% 100.0% Highest degree 4 Graduate Count 55 29 0 84 Expected Count 43.7 37.2 3.1 84.0 % within degree 65.5% 34.5% .0% 100.0% Highest degree Total Count 467 397 33 897 Expected Count 467.0 397.0 33.0 897.0 % within degree 52.1% 44.3% 3.7% 100.0% Highest degree Warning: The chi-square test requires that all observations be independent. This means that each case can appear in only one cell of the table. For example, if you apply 2 different treatments to the same patients and classify them both times as improved or not improved, you can’t analyze the data with the chi-square test of independence.
Computing Expected Values You use the chi-square test to determine if your observed results are unlikely if the 2 variables are independent in the population. 2 variables are independent if knowing the value of one variable tells you nothing about the value of the other variable. The level of education one attains and one’s perception of life are independent if the probability of any level of educational attainment/perception of life combination is the product of the probability of that level of educational attainment times the probability of that perception of life. For example, under the independence assumption, the probability of being a college graduate and finding life exciting is:
P = Probability(bachelor degree) x Probability(life exciting)
P = 143/897 x 467/897 = .083
If the null hypothesis is true, you expect to find in your table 74 excited people with bachelor’s degrees. You see this expected value in the row labeled Expected Count in the table above
The chi-square test is based on comparing these 2 counts: the observed number of cases in a cell and the expected number of cases in a cell if the 2 variables are independent. The Pearson chi-square statistic is:
X2 = ∑ (observed-expected) 2/expected
TIP 24 By examining the differences between observed and expected values in the cells [the residuals], you can see where the independence model falls. You can examine actual residuals and residuals standardized by estimates of their variability to help you pinpoint departures from independence by requesting them in the Cells dialog box of the Analyze/Descriptive Statistics/Crosstabs procedure.
Determining the Observed Significance Level From the calculated chi-square value, you can estimate how often in a sample you would expect to see a chi-square value at least as large as the one you observed if the independence hypothesis is true in the population. If the observed significance level is small, enough you reject the null hypothesis that the 2 variables are independent. The value of chi-square depends on the number of rows and columns in the table. The degrees of freedom for the chi-square statistic is calculated by finding the product of one fewer than the number of rows and one fewer than the number of columns. [the degrees of freedom is the number of cells in a table that can be arbitrarily filled when the row and column totals are fixed.] In this example, the degrees of freedom is 6.
From the table below, you see that the observed significance level for the Pearson chi- square is 0.000, so you can reject the null hypothesis that level of educational attainment and perception of life are independent. Chi-Square Tests
Asymp. Sig. Value df (2-sided) Pearson Chi-Square 34.750a 8 .000 Likelihood Ratio 37.030 8 .000 Linear-by-Linear 29.373 1 .000 Association N of Valid Cases 897 a. 2 cells (13.3%) have expected count less than 5. The minimum expected count is 2.43.
Warning: A conservative rule for use of the chi-square test requires that the expected values in each cell be greater than 1 and that most cells have expected values greater than 5. After SPSS displays the pivot table with the statistics, it displays the number of celss with expected values less than 5 and the minimum expected count. If more than 20% of your cells have expected values less than 5, you should combine categories, if that makes sense for your table, so that most expected values are greater than 5.
Examining Additional Statistics SPSS displays several statistics in addition to the Pearson chi-square when you ask for a chi-square test as shown above. The likelihood-ratio-chi-square has a different mathematical basis than the Pearson chi-square, but for large sample sizes, it is close in value to the Pearson chi-square. It is seldom that these 2 statistics will lead you to different conclusions. The linear-by-linear association statistic is also known as the Mantel-Haenszel chi-square. It is based on the Pearson correlation coefficient. It tests whether there is a linear association between the 2 variables. You SHOULD NOT use this statistic for nominal variables. For ordinal variables, the test is more likely to detect a linear association between the variables than is the Pearson-chi-square test; it is more powerful. A continuity-corrected-chi-square [not shown here] is shown for tables with 2 rows and 2 columns. Some statisticians claim that this leads to a better estimate of the observed significance level, but the claim is disputed. Fisher’s exact test [not shown here] is calculated if any expected value in a 2 by 2 table is < 5. You get exact probabilities of obtaining the observed table or one more extreme if the 2 variables are independent and the marginals are fixed. That is, the number of cases in the rows and columns of the table are determined in advance by the researcher.
Warning: The Mantel-Haenszel test is calculated using the actual values of the row and column variables, so if you coded 3 unevenly spaced dosages of a drug as 1, 2, and 3, those values are used for the computations. Are Proportions Equal? A special case of the chi-square test for independence is the test that several proportions are equal. For example, you want to test whether the % of people who report themselves to be very happy has changed during the time that the GSS has been conducted. The figure below is a crosstabulation of the % of people who say were very happy for each of the decades. This uses the aggregatedgss.sav file. Almost 35% of the people questioned in the 1970s claimed that they were very happy, compared to 31% in this millennium.
happy GENERAL HAPPINESS * decade decade of survey Crosstabulation
decade decade of survey 1 1972-1979 2 1980-1989 3 1990-1999 4 2000-2002 Total happy GENERAL 1 VERY HAPPY Count 3637 4475 4053 1296 13461 HAPPINESS Expected Count 3403.4 4516.7 4211.5 1329.4 13461.0 % within decade 34.3% 31.8% 30.9% 31.3% 32.1% decade of survey 2 PRETTY HAPPY Count 6977 9611 9081 2850 28519 Expected Count 7210.6 9569.3 8922.5 2816.6 28519.0 % within decade 65.7% 68.2% 69.1% 68.7% 67.9% decade of survey Total Count 10614 14086 13134 4146 41980 Expected Count 10614.0 14086.0 13134.0 4146.0 41980.0 % within decade 100.0% 100.0% 100.0% 100.0% 100.0% decade of survey
Calculating the Chi-Square Statistic If the null hypothesis is true, you expect 32.1% of people to be very happy in each decade, the overall very happy rate. You calculate the expected number in each decade by multiplying the total number of people questioned in each decade by 32.1%. The expected number of not very happy people is 67.9% multiplied by the number of people in each decade. These values are shown in the table above. The chi-square statistic is calculated in the usual fashion.
From the table below, you see that the observed significance level for the chi-square statistic is < .001, leading you to reject the null hypothesis that in each decade people are equally likely to describe themselves as very happy. Notice that the difference between years isn’t very large; the largest % is 34.3% for the 1970s, while the smallest is 30.9% for the 1990s. the sample sizes in each group are very large, so even small differences are statistically significant, although they may have little practical implication.
Chi-Square Tests
Asymp. Sig. Value df (2-sided) Pearson Chi-Square 34.180a 3 .000 Likelihood Ratio 33.974 3 .000 Linear-by-Linear 25.746 1 .000 Association N of Valid Cases 41980 a. 0 cells (.0%) have expected count less than 5. The minimum expected count is 1329.43. Introducing a Control Variable To see whether both men and women experienced changes in happiness during this time period, you can compute the chi-square statistic separately for men and for women, as shown below:
Go to Analyze, then Descriptive Statistics, then Crosstabs, then put the variable happy in the row box and decade in the column box, then the variable sex into layer 1 of 1, then select under the cells tab in the crosstabs dialog box, the boxes marked observed and expected counts and column %, then select ok and go back and select the statistics box in order to order a chi- square test.
Chi-Square Tests
sex RESPONDENTS Asymp. Sig. SEX Value df (2-sided) 1 Male Pearson Chi-Square 3.677a 3 .298 Likelihood Ratio 3.668 3 .300 Linear-by-Linear .901 1 .343 Association N of Valid Cases 18442 2 Female Pearson Chi-Square 42.987b 3 .000 Likelihood Ratio 42.712 3 .000 Linear-by-Linear 35.904 1 .000 Association N of Valid Cases 23538 a. 0 cells (.0%) have expected count less than 5. The minimum expected count is 586.01. b. 0 cells (.0%) have expected count less than 5. The minimum expected count is 742.96.
You see that for men, you can’t reject the null hypothesis that happiness has not changed with time. You can reject the null hypothesis for women. From the line plot in the graph below, you see that in the sample, happiness decreases with time for women, but not for men. You can also graph the information. See the graph below, but also note how to obtain the graph.
Go to the graphs menu, choose line, then select the multiple icon and summaries for groups of cases, and then click define. Next move decade inot the category axis box and sex into the define lines by box in the dialog box that appears. Select other statistic, then move happy into the variable list, and then click change statistic. In the statistic subdialog box, select % inside and type 1 into both the low and high text boxes. Click continue, and then click OK. 36 RESPONDENTS SEX Male Female
35 S S E N I
P 34 P A H
L
A 33 R E N E G
) 32 1 , 1 ( n i % 31
30
1972-1979 1980-1989 1990-1999 2000-2002 decade of survey
Cases weighted by number of cases
Measuring Change: McNemar Test The chi-square test can also be used to test hypotheses about change when the same people or objects are observed at two different times. For example, the table below is a crosstabulation of whether a person voted in 1996 and whether he or she voted in 2000. [See gssdata.sav file] vote00 DID R VOTE IN 2000 ELECTION * vote96 DID R VOTE IN 1996 ELECTION Crosstabulation
Count vote96 DID R VOTE IN 1996 ELECTION 2 DID 1 VOTED NOT VOTE Total vote00 DID R VOTE 1 VOTED 1539 151 1690 IN 2000 ELECTION 2 DID NOT VOTE 187 502 689 Total 1726 653 2379
An interesting question is whether people were more likely to vote in one of the years than the other. The cases on the diagonal of the table don’t provide any information because they behaved similarly in both elections. You have to look at the off-diagonal cells, which correspond to people who voted in one election but not the other. If the null hypothesis that likelihood of voting did not change is true, a case should be equally likely tofallinto either of the 2 off-diagonal cells. The binomial distribution is used to calculate the exact probability of observing a split between the 2 off-diagonal cells at least as unequal as the one observed, if cases in the population are equally likely to fall into either off-diagonal cell. This test is called the McNemar test.
Chi-Square Tests
Exact Sig. Value (2-sided) McNemar Test .057a N of Valid Cases 2379 a. Binomial distribution used.
McNemar’s test can be calculated for a square table of any size to test whether the upper half and the lower half of a square table are symmetric. This test is labeled in the table above. For tables with more than 2 rows and columns, it is labeled the McNemar-Bowker test. From the figure below, you see that you can’t reject the null hypothesis that people who voted in only one of the 2 elections were equally likely to vote in another.
Warning: Since the same person is asked whether he or she voted in 1996 and whether he or she voted in 2000, you can’t make a table in which the rows are years and the columns are whether he or she voted. Each case would appear twice in such a table.
How Strongly are 2 Variables Related? If you reject the null hypothesis that 2 variables are independent, you may want to describe the nature and strength of the relationship between the 2 variables. There are many statistical indexes that you can use to quantify the strength of the relationship between 2 variables in a cross-classification. No single measure adequately summarizes all possible types of association. Measures vary in the way they define perfect and intermediate association and in the way they are interpreted. Some measures are used only when the categories of the variables can be ordered from lowest to highest on some scale.
Warning: Don’t compute a large number of measures and then report the most impressive as if it were the only one examined.
You can test the null hypothesis that a particular measure of association is 0 based on an approximate T statistic shown in the output. If the observed significance level is small enough, you reject the null hypothesis that the measure is 0. TIP 25 Measures of association should be calculated with as detailed data as possible. Don’t combine categories with small numbers of cases, as was suggested above for the chi- square test of independence.
FINAL NOTE: IF YOU WISH TO DO MEASURES OF ASSOCIATION TO DETERMINE HOW STRONGLY 2 VARIABLES ARE RELATED, THEN PLEASE SEE ME AND ASK FOR ASSISTANCE IF YOU HAVE ANY DIFFICULTIES ON YOUR OWN.