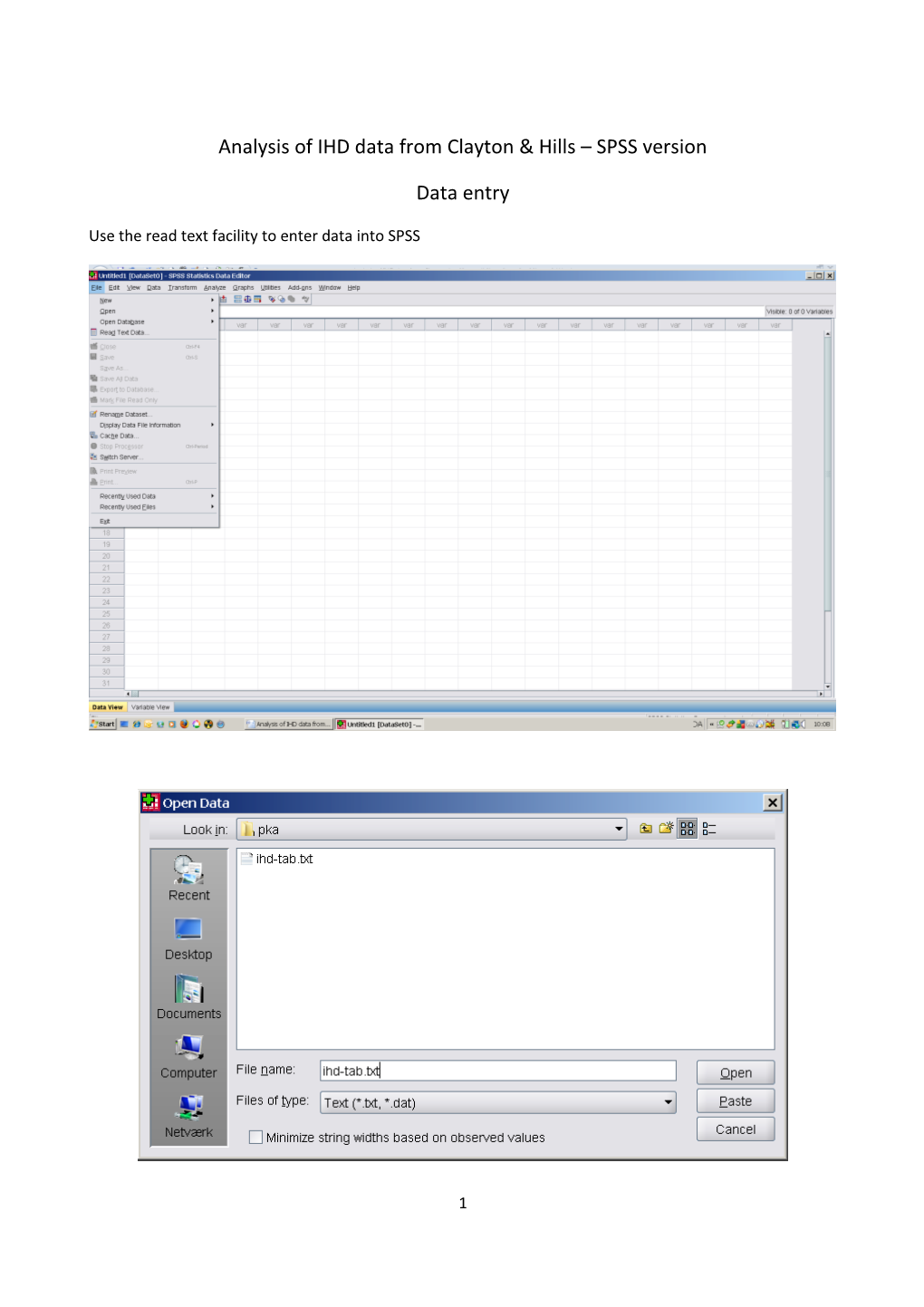
Analysis of IHD Data from Clayton & Hills SPSS Version

Analysis of IHD data from Clayton & Hills – SPSS version

Data entry

Use the read text facility to enter data into SPSS

1 Select “Next” and change the answer concerning variable names at the top of the file from the default “No” to “Yes” in the next dialog form

Select “next” and on the forms for Step 3 through 5

2 3 The data format will be wrong for the pyrs variable since the numbers in the data set uses dots instead of commas. You cannot correct it here, but it is possible to do so after you have selected “Finish” in the final Import Wizard form below.

4 The variable view after test import.

Note that pyrs is a string variable. To change it to a numerical you have to change the variable type to “Comma”. The decimal places need to be equal to 1 for this variable. You should also, of course enter category labels for Sex and Age (not shown here).

Save the data as IHD-TAB such that you do not have to read data again the next time you want to look at it.

5 6 Poisson regression

Important: You need to use the information on person-years (pyrs) as an offset during the Poison regression. The way, SPSS has been set up, the offset variable has to be the logarithm of the person-years.

Before you do anything else you must therefore create a new variable,

Lnpyrs = ln(pyrs)

Having done this, select Generalized linear models to do a Poisson regression

7 The Poisson regression model and analysis must be defined on a number of forms. The first of these is shown below. Note that the OK button has been disabled. It is not clearly shown on the form, but the “OK” to “Help” buttons is not a part of the specific page that you are looking at. Do not press the OK button just because you think that you have entered all the information required. The “Ok” button should first be pressed when you have been through all the pages.

We have selected Poisson loglinear models for this analysis. Many other options are available. At some point you should select Custom and look at all the distribution and link options.

You should also click on the help button to see what they are offering in terms of online help. Sice we know that students never do that when we suggest it we show below what SPS is saying about the analyses. Read it before you proceed!

8 Generalized Linear Models

Generalized Linear Models,Generalized Linear Models,Generalized Linear Models link function,link function,link function

The generalized linear model expands the general linear model so that the dependent variable is linearly related to the factors and covariates via a specified link function. Moreover, the model allows for the dependent variable to have a non-normal distribution. It covers widely used statistical models, such as linear regression for normally distributed responses, logistic models for binary data, loglinear models for count data, complementary log-log models for interval-censored survival data, plus many other statistical models through its very general model formulation.

Examples. A shipping company can use generalized linear models to fit a Poisson regression to damage counts for several types of ships constructed in different time periods, and the resulting model can help determine which ship types are most prone to damage. Show me

A car insurance company can use generalized linear models to fit a gamma regression to damage claims for cars, and the resulting model can help determine the factors that contribute the most to claim size. Show me

Medical researchers can use generalized linear models to fit a complementary log-log regression to interval-censored survival data to predict the time to recurrence for a medical condition. Show me

Generalized Linear Models Data Considerations

To Obtain a Generalized Linear Model

The Type of Model tab allows you to specify the distribution and link function for your model, providing short cuts for several common models that are categorized by response type.

Model Types

Distribution

Link Functions

This procedure pastes GENLIN command syntax.

See GENLIN Algorithms for computational details for this procedure. Related Topics

Generalized Linear Models Response

9 Generalized Linear Models Predictors Generalized Linear Models Model Generalized Linear Models Estimation Generalized Linear Models Statistics Generalized Linear Models EM Means Generalized Linear Models Save Generalized Linear Models Export GENLIN Command Additional Features GENLIN The different pages will be shown below. You do not need all of them to set up the analysis, so this is just to give you an idea about all the options available.

Response

Enter “Cases” as the dependent variable here.

Note that “OK” is enabled. Do not press it. You have not defined the complete model yet.

10 Predictors

The independent variables and the offset are defined on this page. Factors are independent categorical variables. Covariates are quantitative (interval or ratio scale) independent variables. There are no variables of this kind in this example, so the use of such variables cannot be illustrated here.

Pyrs is the offset variable.

Do not click on the Ok button yet. The model is not ready!

11 This page works exactly as the model form in the SPSS program for general linear models except that the default options here make more sense that the default options for the general linear models. Select the independent variables from the list to the left and create model terms (main effects and/or interactions)

12 Estimation

The model-based estimates are maximum likelihood estimate. There are several ways that you can change the way SPSS is supposed to find the estimates of the model.

One thing you must do is to turn the “get initial values for parameter estimates from a dataset” off!

Apart from that, don’t change anything here unless the teacher has told you about these options.

13 Statistics

This is where you tell the program about the output you require from the analysis. In addition to the default options we have selected exponential parameter estimates in order to obtain rate ratios.

Output will be described below.

14 Estimated means

This page can be used to defined tables with estimated means. We have not done this here since it is not part of the exrcise, but you may want to try it anyway.

15 Saving estimates and residuals

Select what you need. The default is not to save anything.

16 Export estimates of models

You may export estimates of model parameters. Default, of course, is not to do anything. Since I do not know what XML is, I would never select this anyway.

17 Output

First, the spss syntax generated by the graphical user interface.

* Generalized Linear Models. GENLIN cases BY exposure age (ORDER=ASCENDING) /MODEL exposure age INTERCEPT=YES OFFSET=pyrs DISTRIBUTION=POISSON LINK=LOG /CRITERIA METHOD=FISHER(1) SCALE=1 COVB=MODEL MAXITERATIONS=100 MAXSTEPHALVING=5 PCONVERGE=1E-006(ABSOLUTE) SINGULAR=1E- 012 ANALYS ISTYPE=3(WALD) CILEVEL=95 CITYPE=WALD LIKELIHOOD=FULL /MISSING CLASSMISSING=EXCLUDE /PRINT CPS DESCRIPTIVES MODELINFO FIT SUMMARY SOLUTION (EXPONENTIATED) LMATRIX.

Then information on then model

18 Then statistical tests.

The goodness of fit test is a test against the saturated model with interaction between exposure and age.For som reason, spss does not want to report p-values of the chi squared test. Since the chi squares are les than the degrees o freedom, it is obvious that the test is insignificant.

19 The omnibus test is a test of the model with no effect of exposure and age against the current model (in this case, the main effect model where both age and exposure has an effect)

The test of Model effects are the tests of each of the separate factors. Ge appears to be insignificant here.

20 Finally the parameter estimates including the rate ratios

The table above discloses a very inconvenient feature of some of the SPSS procedures. In some of these it is regarded as given that the reference category for calculation of effect measures always is the last category. To obtain rate ratios with non-exposure and age = 40-49 as reference you have to create new variables (INVexp = inverted exposure) and INVage = inverted age, where categories are reordered). Having done so, all the test results are as before, but the estimates are as follows:

To solve the second question you have to add the INVage*INVexp interaction to the model in the on the MODL page and then click on OK. We suggest that you do this yourself.