1. the Gell-Mann Nishijima Formula, Q = I3 + B + S /2 , Relates the Third Component Of

Problem Set 1 Physics 357/457

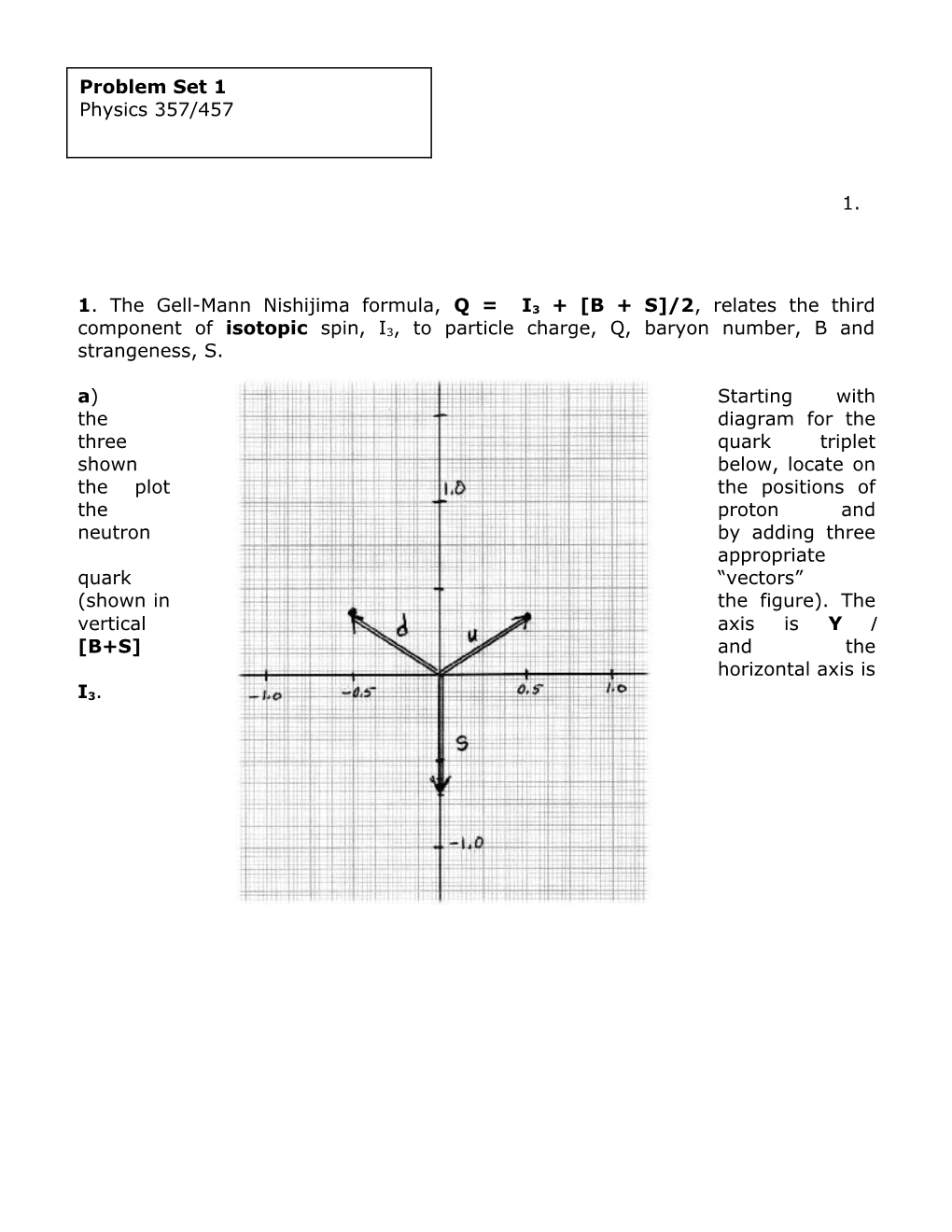
1. The Gell-Mann Nishijima formula, Q = I3 + [B + S]/2, relates the third component of isotopic spin, I3, to particle charge, Q, baryon number, B and strangeness, S. a) Starting with the diagram for the three quark triplet shown below, locate on the plot the positions of the proton and neutron by adding three appropriate quark “vectors” (shown in the figure). The vertical axis is Y  [B+S] and the horizontal axis is

b). Using the same plot, draw the vectors representing the antiparticles of the u, d and s quarks. Label the vectors with the particle name. (10 points)

2. a) Using the following rule, usd => add (in this order) u vector + s vector + d vector, locate on the plot below the end point of the vector sum for the following 10 vector sums: uuu, uud, udd, ddd, sss, suu, sdd, ssu, ssd, uds. Draw a large circle at each location and label with uuu, uud, etc. 3

b) Locate and label (with udu, dud, etc. ) on the plot below the endpoint of the following sums: udu, dud, usu, dsd, sds, sus, dus, sud (8 particles) Note that so far, no sequence of the three vectors has been repeated. 4

c) Repeat b) using the plot above for the following sums: duu, ddu, uus, dds, uss, dss, dsu, sdu (8 particles). Still no sequences are repeated. d) Finally, locate the last usd sum. This is a singlet. e) Name the dimensions of the “multiplets” you have so far identified. How many total (composite) qqq particle sequences have you found?

You should have successfully located all possible 3-quark composites for the the 8-fold way. A” multiplet” generally refers to particles which have the same spin and almost the same mass. One could have several decuplets, for example. They would differ in mass and/or spin. 5 3a) Repeat 2b) for all the quark-antiquark vector sums (using only u d and s) on the plot below.

3b) You should see an octet (8) and a singlet (1) totalling 3x3 = 8 + 1 = 9 total states. Identify these two multiplets (the 8 and the 1) on your plot. The 8 should contain composites which match the properties of the pions. Indicate these locations on your plot.

You will find in Lecture 2 tables which identify in detail the experimentally observed “composite particles” which “match” the multiplets you have generated. They are called the baryon decuplet, the baryon octet and the meson octet.