41. Determination of the Mass of Jupiter from Observations of 10 Hygiea During 1932-1969
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

(704) Interamnia from Its Occultations and Lightcurves
International Journal of Astronomy and Astrophysics, 2014, 4, 91-118 Published Online March 2014 in SciRes. http://www.scirp.org/journal/ijaa http://dx.doi.org/10.4236/ijaa.2014.41010 A 3-D Shape Model of (704) Interamnia from Its Occultations and Lightcurves Isao Satō1*, Marc Buie2, Paul D. Maley3, Hiromi Hamanowa4, Akira Tsuchikawa5, David W. Dunham6 1Astronomical Society of Japan, Yamagata, Japan 2Southwest Research Institute, Boulder, USA 3International Occultation Timing Association, Houston, USA 4Hamanowa Astronomical Observatory, Fukushima, Japan 5Yanagida Astronomical Observatory, Ishikawa, Japan 6International Occultation Timing Association, Greenbelt, USA Email: *[email protected], [email protected], [email protected], [email protected], [email protected], [email protected] Received 9 November 2013; revised 9 December 2013; accepted 17 December 2013 Copyright © 2014 by authors and Scientific Research Publishing Inc. This work is licensed under the Creative Commons Attribution International License (CC BY). http://creativecommons.org/licenses/by/4.0/ Abstract A 3-D shape model of the sixth largest of the main belt asteroids, (704) Interamnia, is presented. The model is reproduced from its two stellar occultation observations and six lightcurves between 1969 and 2011. The first stellar occultation was the occultation of TYC 234500183 on 1996 De- cember 17 observed from 13 sites in the USA. An elliptical cross section of (344.6 ± 9.6 km) × (306.2 ± 9.1 km), for position angle P = 73.4 ± 12.5˚ was fitted. The lightcurve around the occulta- tion shows that the peak-to-peak amplitude was 0.04 mag. and the occultation phase was just be- fore the minimum. -

Surface Composition of Icy Asteroids and the Special Case of Ceres
Surface composition of icy asteroids and the special case of Ceres P. Vernazza (Laboratoire d’Astrophysique de Marseille) March 15, 2017 SOFIA Tele-Talk Examples of asteroids with Compositional links between asteroids and meteorites meteoritic analogues Falls Mass in the asteroid belt 6.2% 9.6% 80.0% 8.4% 1.9% 1.0% 1.1% 0.4% 2.5% 0.1% 1.5% 7.0% 4.6% 3.3% Total Total ~98% ~30% Vernazza & Beck 2016 ~2/3 of the mass of the asteroid belt seems absent from our meteorite collections 6 asteroid types, representing ~2/3 of the main belt mass (DeMeo & Carry 2013), are presently unconnected to meteorites. Asteroid spectral properties (DeMeo et al. 2009) Metamorphosed CI/CM chondrites as analogues of most B, C, Cb, Cg types? (1) Metamorphosed CI/CM chondrites as analogues of most B, C, Cb, Cg types? (2) This is very unlikely because: a) Metamorphosed CI/CM chondrites represent 0.2% of the falls whereas B, C, Cb and Cg type represent ~50% of the mass of the belt b) Metamorphosed CI/CM chondrites possess a significantly higher density (2.5-3 g/cm3) than those asteroid types (0.8-1.5 g/cm3) c) Metamorphosed CI/CM chondrites possess different spectral properties in the mid-infrared with respect to those asteroid types Why are most B, C, Cb, Cg, P and D types unsampled by our meteorite collections? The lack of samples for these objects within our collections may stem from the fact that they are volatile-rich as implied by their low density (0.8-2 g/cm3) and their comet-like activity in some cases. -

Sciences, Is the Discovery of Twenty-Two Minor Planets Commonly Known As the Watson Asteriods
ASTRONOMY: A. O. LEUSCHNER 67 ADMISSIONS TO SICK REPORT-Concluded UNITED STATES NUMBERS opFr White Colored INTERNA- TIONAL CLASSIFICA- Mean strength..................................................... 545,518 13,150 TIONT Causes of admission to sick report Ratio perstrength1000 of mean 00-02, 07,15, 16,24- 27,29- 31,49, 57,58, 60,61, Traumatisms, others ............................... 9.14 10.04 63-65, 70-72, 74,76- 78,82- 84,97- 99 80 Sunstroke.. 0.04 0.08 Total for diseases................................. 882.51 1064.41 Total for external causes.. 91.69 90.42 Grand total................... ................ 974.19 1154.83 PERTURBATIONS AND TABLES OF THE MINOR PLANETS DISCOVERED BY JAMES C. WATSON BY ARMIN 0. LEUSCHNER BERKELEY ASTRONOMICAL DEPARTMENT, UNIVERSITY OF CALIFORNIA Read before the Academy, April 16, 1916 Among the many important contributions to Astronomical Science by James C. Watson, one of the original members of the National Academy of Sciences, is the discovery of twenty-two minor planets commonly known as the Watson asteriods. The first of these, (79) Eurynome, was discovered at Ann Arbor on September 14, 1863, and the last, (179) Klytaemnestra, on November 11, 1877, three years before his death. By his will a fund was bequeathed in trust to the National Academy of Sciences for the purpose of promoting astronomical research. One of the objects specifically designated was the construction of tables of the perturbations of the minor planets dis- covered by the testator. From the beginning Prof. Simon Newcomb was a Downloaded by guest on September 30, 2021 68 ASTRONOMY: A. O. LEUSCHNER member of the board of Watson Trustees; later he became chairman of the board, and remained in that capacity on the board until his death in 1908, being succeeded by Prof. -

Hydrated Minerals on Asteroids: the Astronomical Record
Hydrated Minerals on Asteroids: The Astronomical Record A. S. Rivkin, E. S. Howell, F. Vilas, and L. A. Lebofsky March 28, 2002 Corresponding Author: Andrew Rivkin MIT 54-418 77 Massachusetts Ave. Cambridge MA, 02139 [email protected] 1 1 Abstract Knowledge of the hydrated mineral inventory on the asteroids is important for deducing the origin of Earth’s water, interpreting the meteorite record, and unraveling the processes occurring during the earliest times in solar system history. Reflectance spectroscopy shows absorption features in both the 0.6-0.8 and 2.5-3.5 pm regions, which are diagnostic of or associated with hydrated minerals. Observations in those regions show that hydrated minerals are common in the mid-asteroid belt, and can be found in unex- pected spectral groupings, as well. Asteroid groups formerly associated with mineralogies assumed to have high temperature formation, such as MAand E-class asteroids, have been observed to have hydration features in their reflectance spectra. Some asteroids have apparently been heated to several hundred degrees Celsius, enough to destroy some fraction of their phyllosili- cates. Others have rotational variation suggesting that heating was uneven. We summarize this work, and present the astronomical evidence for water- and hydroxyl-bearing minerals on asteroids. 2 Introduction Extraterrestrial water and water-bearing minerals are of great importance both for understanding the formation and evolution of the solar system and for supporting future human activities in space. The presence of water is thought to be one of the necessary conditions for the formation of life as 2 we know it. -
Iso and Asteroids
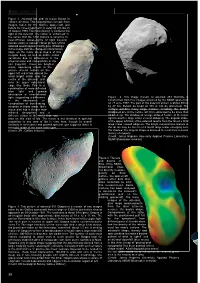
r bulletin 108 Figure 1. Asteroid Ida and its moon Dactyl in enhanced colour. This colour picture is made from images taken by the Galileo spacecraft just before its closest approach to asteroid 243 Ida on 28 August 1993. The moon Dactyl is visible to the right of the asteroid. The colour is ‘enhanced’ in the sense that the CCD camera is sensitive to near-infrared wavelengths of light beyond human vision; a ‘natural’ colour picture of this asteroid would appear mostly grey. Shadings in the image indicate changes in illumination angle on the many steep slopes of this irregular body, as well as subtle colour variations due to differences in the physical state and composition of the soil (regolith). There are brighter areas, appearing bluish in the picture, around craters on the upper left end of Ida, around the small bright crater near the centre of the asteroid, and near the upper right-hand edge (the limb). This is a combination of more reflected blue light and greater absorption of near-infrared light, suggesting a difference Figure 2. This image mosaic of asteroid 253 Mathilde is in the abundance or constructed from four images acquired by the NEAR spacecraft composition of iron-bearing on 27 June 1997. The part of the asteroid shown is about 59 km minerals in these areas. Ida’s by 47 km. Details as small as 380 m can be discerned. The moon also has a deeper near- surface exhibits many large craters, including the deeply infrared absorption and a shadowed one at the centre, which is estimated to be more than different colour in the violet than any 10 km deep. -

Ceres: Astrobiological Target and Possible Ocean World
ASTROBIOLOGY Volume 20 Number 2, 2020 Research Article ª Mary Ann Liebert, Inc. DOI: 10.1089/ast.2018.1999 Ceres: Astrobiological Target and Possible Ocean World Julie C. Castillo-Rogez,1 Marc Neveu,2,3 Jennifer E.C. Scully,1 Christopher H. House,4 Lynnae C. Quick,2 Alexis Bouquet,5 Kelly Miller,6 Michael Bland,7 Maria Cristina De Sanctis,8 Anton Ermakov,1 Amanda R. Hendrix,9 Thomas H. Prettyman,9 Carol A. Raymond,1 Christopher T. Russell,10 Brent E. Sherwood,11 and Edward Young10 Abstract Ceres, the most water-rich body in the inner solar system after Earth, has recently been recognized to have astrobiological importance. Chemical and physical measurements obtained by the Dawn mission enabled the quantification of key parameters, which helped to constrain the habitability of the inner solar system’s only dwarf planet. The surface chemistry and internal structure of Ceres testify to a protracted history of reactions between liquid water, rock, and likely organic compounds. We review the clues on chemical composition, temperature, and prospects for long-term occurrence of liquid and chemical gradients. Comparisons with giant planet satellites indicate similarities both from a chemical evolution standpoint and in the physical mechanisms driving Ceres’ internal evolution. Key Words: Ceres—Ocean world—Astrobiology—Dawn mission. Astro- biology 20, xxx–xxx. 1. Introduction these bodies, that is, their potential to produce and maintain an environment favorable to life. The purpose of this article arge water-rich bodies, such as the icy moons, are is to assess Ceres’ habitability potential along the same lines Lbelieved to have hosted deep oceans for at least part of and use observational constraints returned by the Dawn their histories and possibly until present (e.g., Consolmagno mission and theoretical considerations. -
Rocks in Space Asteroids, Comets and Meteors
Modern Astronomy: Voyage to the Planets Lecture 6 Rocks in Space asteroids, comets and meteors University of Sydney Centre for Continuing Education Autumn 2009 Tonight: • Asteroids – rocks that circle • Comets – rocks that evaporate • Trans-Neptunian objects – really cold rocks • Meteorites – rocks that fall Asteroids The Solar System contains a large number of small bodies, of which the largest are the asteroids. Some orbit the Sun inside the Earth’s orbit, and others have highly elliptical orbits which cross the Earth’s. However, the vast bulk of asteroids orbit the Sun in nearly circular orbits in a broad belt between Mars and Jupiter. An asteroid (or strictly minor planet*) is smaller than major planets, but larger than meteoroids, which are 10m or less in size. * since 2006, these are now officially small solar system bodies, though the term “minor planet” may still be used As of April 2009, there are 212,999 asteroids which have been given numbers; 15190 have been given names. The rate of discovery of new bodies is about 5000 per month. It is estimated there are between 1.1 and 1.9 million asteroids larger than 1 km in diameter. Number of minor planets with orbits (red) and names (green) The largest are 1 Ceres (1000 km in diameter), 2 Pallas (550 km), 4 Vesta (530!km), and 10 Hygiea (410 km). Only 16 asteroids are larger than 240 km in size. Ceres is by far the largest and most massive body in the asteroid belt, and contains approximately a third of the belt's total mass. -

Nasa Technical Memorandum .1
NASA TECHNICAL MEMORANDUM NASA TM X-64677 COMETS AND ASTEROIDS: A Strategy for Exploration REPORT OF THE COMET AND ASTEROID MISSION STUDY PANEL May 1972 .1!vP -V (NASA-TE-X- 6 q767 ) COMETS AND ASTEROIDS: A RR EXPLORATION (NASA) May 1972 CSCL 03A NATIONAL AERONAUTICS AND SPACE ADMINISTRATION Reproduced by ' NATIONAL "TECHINICAL INFORMATION: SERVICE US Depdrtmett ofCommerce :. Springfield VA 22151 TECHNICAL REPORT STANDARD TITLE PAGE · REPORT NO. 2. GOVERNMENT ACCESSION NO. 3, RECIPIENT'S CATALOG NO. NASA TM X-64677 . TITLE AND SUBTITLE 5. REPORT aE COMETS AND ASTEROIDS ___1_ A Strategy for Exploration 6. PERFORMING ORGANIZATION CODE AUTHOR(S) 8. PERFORMING ORGANIZATION REPORT # Comet and Asteroid Mission Study Panel PERFORMING ORGANIZATION NAME AND ADDRESS 10. WORK UNIT NO. 11. CONTRACT OR GRANT NO. 13. TYPE OF REPORT & PERIOD COVERED 2. SPONSORING AGENCY NAME AND ADDRESS National Aeronautics and Space Administration Technical Memorandum Washington, D. C. 20546 14. SPONSORING AGENCY CODE 5. SUPPLEMENTARY NOTES ABSTRACT Many of the asteroids probably formed near the orbits where they are found today. They accreted from gases and particles that represented the primordial solar system cloud at that location. Comets, in contrast to asteroids, probably formed far out in the solar system, and at very low temperatures; since they have retained their volatile components they are probably the most primordial matter that presently can be found anywhere in the solar system. Exploration and detailed study of comets and asteroids, therefore, should be a significant part of NASA's efforts to understand the solar system. A comet and asteroid program should consist of six major types of projects: ground-based observations;Earth-orbital observations; flybys; rendezvous; landings; and sample returns. -

Comets, Asteroids and Zodiacal Light As Seen by ISO ∗
Comets, Asteroids and Zodiacal Light as seen by ISO ∗ Thomas G. M¨uller Max-Planck-Institut f¨ur extraterrestrische Physik, Giessenbachstraße, 85748 Garching, Germany; ([email protected]) P´eter Abrah´´ am Konkoly Observatory, H-1525 P.O. Box 67, Budapest, Hungary; ([email protected]) Jacques Crovisier LESIA, Observatoire de Paris, 5 place Jules Janssen, F-92195 Meudon, France; ([email protected]) Abstract. ISO performed a large variety of observing programmes on comets, asteroids and zodiacal light –covering about 1% of the archived observations– with a surprisingly rewarding scientific return. Outstanding results were related to the exceptionally bright comet Hale-Bopp and to ISO’s capability to study in detail the water spectrum in a direct way. But many other results were broadly recognised: Investigation of cometary molecules, the studies of crystalline silicates, the work on asteroid surface mineralogy, results from thermophysical studies of asteroids, a new determination of the asteroid number density in the main-belt and last but not least, the investigations on the spatial and spectral features of the zodiacal light. Keywords: ISO – asteroids – comets – SSO: solar system objects – zodiacal light – dust Received: 13 July 2004 1. Introduction The comet, asteroid and zodiacal light programme of ISO –without the planets– covered approximately 325 hours, less than 1 % of all ISO observations. Thus, the solar system community did not expect much from this small number of observations with a 60-cm telescope circu- lating just outside the Earth’ atmosphere. Yet, the ISO results made a big impact on our knowledge of objects on our celestial “doorstep”. 11 Guaranteed Time projects and 31 Open Time projects were either dedicated to comets, asteroids and zodiacal light studies or included solar system science aspects. -

Organic Matter and Associated Minerals on the Dwarf Planet Ceres
minerals Review Organic Matter and Associated Minerals on the Dwarf Planet Ceres Maria Cristina De Sanctis 1,* and Eleonora Ammannito 2 1 Istituto di Astrofisica e Planetologia Spaziali, Istituto Nazionale di Astrofisica (INAF), 00133 Rome, Italy 2 Agenzia Spaziale Italiana, Via del Politecnico, 00133 Roma, Italy; [email protected] * Correspondence: [email protected] Abstract: Ceres is the largest object in the main belt and it is also the most water-rich body in the inner solar system besides the Earth. The discoveries made by the Dawn Mission revealed that the composition of Ceres includes organic material, with a component of carbon globally present and also a high quantity of localized aliphatic organics in specific areas. The inferred mineralogy of Ceres indicates the long-term activity of a large body of liquid water that produced the alteration minerals discovered on its surface, including ammonia-bearing minerals. To explain the presence of ammonium in the phyllosilicates, Ceres must have accreted organic matter, ammonia, water and carbon present in the protoplanetary formation region. It is conceivable that Ceres may have also processed and transformed its own original organic matter that could have been modified by the pervasive hydrothermal alteration. The coexistence of phyllosilicates, magnetite, carbonates, salts, organics and a high carbon content point to rock–water alteration playing an important role in promoting widespread carbon occurrence. Keywords: Ceres; asteroids; organics; aliphatics; solar system Citation: De Sanctis, M.C.; Ammannito, E. Organic Matter and Associated Minerals on the Dwarf 1. Ceres: A Dwarf Planet in the Main Belt Planet Ceres. Minerals 2021, 11, 799. -

The Case for Ceres: Report to the Planetary Science Decadal Survey Committee
The Case for Ceres: Report to the Planetary Science Decadal Survey Committee Andrew S. Rivkin (JHU/APL), Julie C. Castillo-Rogez (JPL), Neyda M. Abreu (Penn State Dubois), Erik Asphaug (University of California, Santa Cruz), Andrew F. Cheng (JHU/APL), Beth E. Clark (Ithaca College), Barbara A. Cohen (NASA MSFC), Pamela G. Conrad (JPL), Paul Hayne (UCLA), Ellen S. Howell (Arecibo Observatory), Torrence V. Johnson (JPL), Georgiana Kramer (Bear Fight Center), Jian-Yang Li (University of Maryland), Larry A. Lebofsky (University of Arizona), Lucy F. Lim (University of Maryland), Amy J. Lovell (Agnes Scott College), Dennis L. Matson (JPL), Thomas M. McCord (Bear Fight Center), Lucy-Ann McFadden (University of Maryland), William B. McKinnon (Washington University), Ralph E. Milliken (JPL), William Moore (UCLA), James H. Roberts (JHU/APL), Christopher T. Russell (UCLA), Britney E. Schmidt (UCLA), Mark V. Sykes (PSI), Peter C. Thomas (Cornell University), Mikhail Zolotov (ASU) Contact Author: Andrew Rivkin JHU/APL 443-778-2811 [email protected] Executive Summary Ceres is the largest object in the asteroid belt. With a diameter of 950 km and a density of 2.1 g/cm3 (Table 1), it accounts for one-third of the mass found between Mars and Jupiter. Since the last decadal survey our knowledge of Ceres has blossomed. Observations, modeling, and theory are converging on a paradigm of a severely aqueously altered body with an icy mantle covering a rocky core. Ceres is intermediate in nature between the rocky bodies of the inner solar system and the icy satellites. This paradigm is still in its infancy, however, and recent work has proposed alternatives including an undifferentiated object, and even an origin in the outer solar system. -

Techniques for Asteroid Spectrocopy Marcel Popescu
Techniques for asteroid spectrocopy Marcel Popescu To cite this version: Marcel Popescu. Techniques for asteroid spectrocopy. Earth and Planetary Astrophysics [astro- ph.EP]. Observatoire de Paris; Universitatea Politehnica din Bucuresti, Facultatea de Ştiinţe Aplicate, 2012. English. tel-00785991 HAL Id: tel-00785991 https://tel.archives-ouvertes.fr/tel-00785991 Submitted on 7 Feb 2013 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. OBSERVATOIRE DE PARIS ÉCOLE DOCTORALE D’ASTRONOMIE ET D’ASTROPHYSIQUE D’ÎLE-DE-FRANCE ∗ UNIVERSITATEA POLITHENICA BUCURE¸STI FACULTATEA DE ¸STIIN ¸TE APLICATE DOCTORAL THESIS by Marcel Popescu TECHNIQUES FOR ASTEROID SPECTROSCOPY Defended the 23 Octobre 2012 before the jury: Vasile IFTODE (Universitatea Polithenica Bucure¸sti) President Olivier GROUSSIN (Laboratoire d’Astrophysique de Marseille) Reviewer Petre POPESCU (Institutul Astronomic al Academiei Române) Reviewer Dan DUMITRA¸S (INFLPR, România) Reviewer Jean SOUCHAY (SYRTE - Observatoire de Paris) Examiner Mirel BIRLAN (IMCCE - Observatoire de Paris) Co-Advisor