Some Concepts from Algebra
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

"The Newton Polygon of a Planar Singular Curve and Its Subdivision"
THE NEWTON POLYGON OF A PLANAR SINGULAR CURVE AND ITS SUBDIVISION NIKITA KALININ Abstract. Let a planar algebraic curve C be defined over a valuation field by an equation F (x,y)= 0. Valuations of the coefficients of F define a subdivision of the Newton polygon ∆ of the curve C. If a given point p is of multiplicity m on C, then the coefficients of F are subject to certain linear constraints. These constraints can be visualized in the above subdivision of ∆. Namely, we find a 3 2 distinguished collection of faces of the above subdivision, with total area at least 8 m . The union of these faces can be considered to be the “region of influence” of the singular point p in the subdivision of ∆. We also discuss three different definitions of a tropical point of multiplicity m. 0. Introduction Fix a non-empty finite subset Z2 and any valuation field K. We consider a curve C given by an equation F (x,y) = 0, where A⊂ i j ∗ (1) F (x,y)= aijx y , aij K . ∈ (i,jX)∈A Suppose that we know only the valuations of the coefficients of the polynomial F (x,y). Is it possible to extract any meaningful information from this knowledge? Unexpectedly, many geometric properties of C are visible from such a viewpoint. The Newton polygon ∆=∆( ) of the curve C is the convex hull of in R2. The extended Newton A A2 polyhedron of the curve C is the convex hull of the set ((i, j),s) R R (i, j) ,s val(aij) . -

Kepler's Area Law in the Principia: Filling in Some Details in Newton's
Historia Mathematica 30 (2003) 441–456 www.elsevier.com/locate/hm Kepler’s area law in the Principia: filling in some details in Newton’s proof of Proposition 1 Michael Nauenberg Department of Physics, University of California, Santa Cruz, CA 95064, USA Abstract During the past 30 years there has been controversy regarding the adequacy of Newton’s proof of Prop. 1 in Book 1 of the Principia. This proposition is of central importance because its proof of Kepler’s area law allowed Newton to introduce a geometric measure for time to solve problems in orbital dynamics in the Principia.Itis shown here that the critics of Prop. 1 have misunderstood Newton’s continuum limit argument by neglecting to consider the justification for this limit which he gave in Lemma 3. We clarify the proof of Prop. 1 by filling in some details left out by Newton which show that his proof of this proposition was adequate and well-grounded. 2003 Elsevier Inc. All rights reserved. Résumé Au cours des 30 dernières années, il y a eu une controverse au sujet de la preuve de la Proposition 1 telle qu’elle est formulée par Newton dans le premier livre de ses Principia. Cette proposition est d’une importance majeure puisque la preuve qu’elle donne de la loi des aires de Kepler permit à Newton d’introduire une expression géometrique du temps, lui permettant ainsi de résoudre des problèmes dans la domaine de la dynamique orbitale. Nous démontrons ici que les critiques de la Proposition 1 ont mal compris l’argument de Newton relatif aux limites continues et qu’ils ont négligé de considérer la justification pour ces limites donnée par Newton dans son Lemme 3. -

Absolute Irreducibility of Polynomials Via Newton Polytopes
ABSOLUTE IRREDUCIBILITY OF POLYNOMIALS VIA NEWTON POLYTOPES SHUHONG GAO DEPARTMENT OF MATHEMATICAL SCIENCES CLEMSON UNIVERSITY CLEMSON, SC 29634 USA [email protected] Abstract. A multivariable polynomial is associated with a polytope, called its Newton polytope. A polynomial is absolutely irreducible if its Newton polytope is indecomposable in the sense of Minkowski sum of polytopes. Two general constructions of indecomposable polytopes are given, and they give many simple irreducibility criteria including the well-known Eisenstein’s crite- rion. Polynomials from these criteria are over any field and have the property of remaining absolutely irreducible when their coefficients are modified arbi- trarily in the field, but keeping certain collection of them nonzero. 1. Introduction It is well-known that Eisenstein’s criterion gives a simple condition for a polyno- mial to be irreducible. Over the years this criterion has witnessed many variations and generalizations using Newton polygons, prime ideals and valuations; see for examples [3, 25, 28, 38]. We examine the Newton polygon method and general- ize it through Newton polytopes associated with multivariable polynomials. This leads us to a more general geometric criterion for absolute irreducibility of multi- variable polynomials. Since the Newton polygon of a polynomial is only a small fraction of its Newton polytope, our method is much more powerful. Absolute irre- ducibility of polynomials is crucial in many applications including but not limited to finite geometry [14], combinatorics [47], algebraic geometric codes [45], permuta- tion polynomials [23] and function field sieve [1]. We present many infinite families of absolutely irreducible polynomials over an arbitrary field. These polynomials remain absolutely irreducible even if their coefficients are modified arbitrarily but with certain collection of them nonzero. -

Characterizing and Tuning Exceptional Points Using Newton Polygons
Characterizing and Tuning Exceptional Points Using Newton Polygons Rimika Jaiswal,1 Ayan Banerjee,2 and Awadhesh Narayan2, ∗ 1Undergraduate Programme, Indian Institute of Science, Bangalore 560012, India 2Solid State and Structural Chemistry Unit, Indian Institute of Science, Bangalore 560012, India (Dated: August 3, 2021) The study of non-Hermitian degeneracies { called exceptional points { has become an exciting frontier at the crossroads of optics, photonics, acoustics and quantum physics. Here, we introduce the Newton polygon method as a general algebraic framework for characterizing and tuning excep- tional points, and develop its connection to Puiseux expansions. We propose and illustrate how the Newton polygon method can enable the prediction of higher-order exceptional points, using a recently experimentally realized optical system. As an application of our framework, we show the presence of tunable exceptional points of various orders in PT -symmetric one-dimensional models. We further extend our method to study exceptional points in higher number of variables and demon- strate that it can reveal rich anisotropic behaviour around such degeneracies. Our work provides an analytic recipe to understand and tune exceptional physics. Introduction{ Energy non-conserving and dissipative Isaac Newton, in 1676, in his letters to Oldenburg and systems are described by non-Hermitian Hamiltoni- Leibniz [54]. They are conventionally used in algebraic ans [1]. Unlike their Hermitian counterparts, they are not geometry to prove the closure of fields [55] and are in- always diagonalizable and can become defective at some timately connected to Puiseux series { a generalization unique points in their parameter space { called excep- of the usual power series to negative and fractional ex- tional points (EPs) { where both the eigenvalues and the ponents [56, 57]. -

Newton Polygons
Last revised 12:55 p.m. October 21, 2018 Newton polygons Bill Casselman University of British Columbia [email protected] Newton polygons are associated to polynomials with coefficients in a discrete valuation ring, and they give information about the valuations of roots. There are several applications, among them to the structure of Dieudonne´ modules, the ramification of local field extensions, and the desingularization of algebraic curves in P2. As an exception to a common practice of attribution, Newton polygons were originally introduced by Isaac Newton himself, and how he used them is not so different from how they are used now. He wanted to solve polynomial equations f(x, y)=0 for y as a series in fractional powers of x. For example, to solve yn = x we write simply y = x1/n, and 1/n to solve yn =1+ x set y = xk . X0 k Newton sketched the procedure he had come up with in a letter to Oldenburg. It is quite readable (see p. 126 of [Newton:1959] for the original Latin, p. 145 for an English translation). The diagram he exhibits is not essentially different from the ones drawn today. Newton polygons are perfectly and appropriately named—they are non•trivial, and introduced by Newton. This thread became eventually a method related to desingularizing algebraic curves over C (explained in Chaper IV of [Walker:1950]). My original motivation in writing this essay was to understand the theory of crystals, particularly 5 of § Chapter IV of [Demazure:1970]. But since then I have come across other applications. -

Finsler Metric, Systolic Inequality, Isometr
DISCRETE SURFACES WITH LENGTH AND AREA AND MINIMAL FILLINGS OF THE CIRCLE MARCOS COSSARINI Abstract. We propose to imagine that every Riemannian metric on a surface is discrete at the small scale, made of curves called walls. The length of a curve is its number of wall crossings, and the area of the surface is the number of crossings of the walls themselves. We show how to approximate a Riemannian (or self-reverse Finsler) metric by a wallsystem. This work is motivated by Gromov's filling area conjecture (FAC) that the hemisphere minimizes area among orientable Riemannian sur- faces that fill a circle isometrically. We introduce a discrete FAC: every square-celled surface that fills isometrically a 2n-cycle graph has at least n(n−1) 2 squares. We prove that our discrete FAC is equivalent to the FAC for surfaces with self-reverse metric. If the surface is a disk, the discrete FAC follows from Steinitz's algo- rithm for transforming curves into pseudolines. This gives a combinato- rial proof of the FAC for disks with self-reverse metric. We also imitate Ivanov's proof of the same fact, using discrete differential forms. And we prove a new theorem: the FAC holds for M¨obiusbands with self- reverse metric. To prove this we use a combinatorial curve shortening flow developed by de Graaf-Schrijver and Hass-Scott. The same method yields a proof of the systolic inequality for Klein bottles with self-reverse metric, conjectured by Sabourau{Yassine. Self-reverse metrics can be discretized using walls because every normed plane satisfies Crofton's formula: the length of every segment equals the symplectic measure of the set of lines that it crosses. -

THE WILLIAM LOWELL PUTNAM MATHEMATICAL COMPETITION 1985–2000 Problems, Solutions, and Commentary
AMS / MAA PROBLEM BOOKS VOL 33 THE WILLIAM LOWELL PUTNAM MATHEMATICAL COMPETITION 1985–2000 Problems, Solutions, and Commentary Kiran S. Kedlaya Bjorn Poonen Ravi Vakil 10.1090/prb/033 The William Lowell Putnam Mathematical Competition 1985-2000 Originally published by The Mathematical Association of America, 2002. ISBN: 978-1-4704-5124-0 LCCN: 2002107972 Copyright © 2002, held by the American Mathematical Society Printed in the United States of America. Reprinted by the American Mathematical Society, 2019 The American Mathematical Society retains all rights except those granted to the United States Government. ⃝1 The paper used in this book is acid-free and falls within the guidelines established to ensure permanence and durability. Visit the AMS home page at https://www.ams.org/ 10 9 8 7 6 5 4 3 2 24 23 22 21 20 19 AMS/MAA PROBLEM BOOKS VOL 33 The William Lowell Putnam Mathematical Competition 1985-2000 Problems, Solutions, and Commentary Kiran S. Kedlaya Bjorn Poonen Ravi Vakil MAA PROBLEM BOOKS SERIES Problem Books is a series of the Mathematical Association of America consisting of collections of problems and solutions from annual mathematical competitions; compilations of problems (including unsolved problems) specific to particular branches of mathematics; books on the art and practice of problem solving, etc. Committee on Publications Gerald Alexanderson, Chair Problem Books Series Editorial Board Roger Nelsen Editor Irl Bivens Clayton Dodge Richard Gibbs George Gilbert Art Grainger Gerald Heuer Elgin Johnston Kiran Kedlaya Loren Larson Margaret Robinson The Contest Problem Book VII: American Mathematics Competitions, 1995-2000 Contests, compiled and augmented by Harold B. -

Galois Groups of Eisenstein Polynomials Whose Ramification
ON RAMIFICATION POLYGONS AND GALOIS GROUPS OF EISENSTEIN POLYNOMIALS CHRISTIAN GREVE AND SEBASTIAN PAULI Abstract. Let '(x) be an Eisenstein polynomial of degree n over a local field and α be a root of '(x). Our main tool is the ramification polygon of '(x), that is the Newton polygon of ρ(x) = '(αx + α)=(αnx). We present a method for determining the Galois group of '(x) in the case where the ramification polygon consists of one segment. 1. Introduction Algorithms for computing Galois groups are an important tool in constructive number theory. The commonly used algorithms for computing Galois groups of polynomials over Q (and Q(t)) are based on the method of Stauduhar [20]. Considerable progress has been made in this area over the last ten years. For local fields however, that is for fields K complete with respect to a non-archimedian exponential valuation ν with residue class field K of characteristic p 6= 1, there is no general algorithm. As the Galois groups of unramified extensions are explicitly known, we concentrate the Galois groups of totally ramified extensions. These can be generated by an Eisenstein poly- n Pn−1 i nomial, that is a polynomial '(x) = x + i=0 'ix 2 OK[x] with ν('0) = 1 and ν('i) ≥ 1 for 1 ≤ i ≤ n − 1. We denote by α a root of '(x) in an algebraic closure K of K. If p does not divide the degree of '(x) the extension K(α) is tamely ramified and can be generated by a pure polynomial. We show how this pure polynomial can be obtained and recall the (well known) explicit description of its Galois group (see section 2). -

Bibliography for Arithmetic Dynamical Systems
Bibliography for Arithmetic Dynamics Joseph H. Silverman May 5, 2020 This document lists a wide variety of articles and books in the area of arithmetic dynamics. It also includes some additional material that was referenced in The Arith- metic of Dynamical Systems (Springer-Verlag GTM 241) and some miscellaneous ar- ticles and books that I’ve referenced in my own work. Note that the numbering in this document does not match the numbering of references in GTM 241. Further note that I do not automatically update ArXiv preprints when they appear. Most recent pub- lished articles in arithmetic dynamics can be found by searching the 37P category on MathSciNet. References [1] N. Abarenkova, J.-C. Angles` d’Auriac, S. Boukraa, S. Hassani, and J.-M. Maillard. Topological entropy and Arnold complexity for two-dimensional mappings. Phys. Lett. A, 262(1):44–49, 1999. [2] W. Abram and J. C. Lagarias. Intersections of multiplicative translates of 3-adic cantor sets, 2013. arXiv:1308.3133. [3] R. L. Adler, A. G. Konheim, and M. H. McAndrew. Topological entropy. Trans. Amer. Math. Soc., 114:309–319, 1965. [4] L. V. Ahlfors. Complex Analysis. McGraw-Hill Book Co., New York, 1978. [5] F. Ahmad, R. L. Benedetto, J. Cain, G. Carroll, and L. Fang. The arithmetic basilica: a quadratic PCF arboreal Galois group, 2019. arXiv:1909.00039. [6] O. Ahmadi. A note on stable quadratic polynomials over fields of characteristic two, 2009. arXiv:0910.4556. [7] O. Ahmadi, F. Luca, A. Ostafe, and I. E. Shparlinski. On stable quadratic polynomials. Glasg. Math. J., 54(2):359–369, 2012. -

UC Davis Faculty
UC Davis Faculty Title Lectures on the Topological Recursion for Higgs Bundles and Quantum Curves Permalink https://escholarship.org/uc/item/858382hb Authors Dumitrescu, O Mulase, M Publication Date 2018 DOI 10.1142/9789813229099_0003 Peer reviewed eScholarship.org Powered by the California Digital Library University of California LECTURES ON THE TOPOLOGICAL RECURSION FOR HIGGS BUNDLES AND QUANTUM CURVES OLIVIA DUMITRESCU AND MOTOHICO MULASE Abstract. The paper aims at giving an introduction to the notion of quantum curves. The main purpose is to describe the new discovery of the relation between the following two disparate subjects: one is the topological recursion, that has its origin in random matrix theory and has been effectively applied to many enumerative geometry problems; and the other is the quantization of Hitchin spectral curves associated with Higgs bundles. Our emphasis is on explaining the motivation and examples. Concrete examples of the direct relation between Hitchin spectral curves and enumeration problems are given. A general geometric framework of quantum curves is also discussed. Contents 1. Introduction 2 1.1. On the other side of the rainbow 2 1.2. Quantum curves, semi-classical limit, and the WKB analysis 11 1.3. The topological recursion as quantization 13 1.4. Non-Abelian Hodge correspondence and quantum curves 16 1.5. The Lax operator for Witten-Kontsevich KdV equation 19 1.6. All things considered 21 2. From Catalan numbers to the topological recursion 24 2.1. Counting graphs on a surface 25 2.2. The spectral curve of a Higgs bundle and its desingularization 29 2.3. The generating function, or the Laplace transform 31 2.4. -

Final Report (PDF)
Women in Numbers 4 Chantal David (Concordia University) Michelle Manes (University of Hawaii at Manoa) Jennifer Balakrishnan (Boston University) Bianca Viray (University of Washington) August 13-18, 2017 1 Conference at BIRS 1.1 Rationale and Goals The first Women in Numbers workshop was held at BIRS in 2008, with the explicit goals of increasing the participation of women in number theory research and highlighting the contributions of women who were already doing high-quality research in the field. In their original proposal, the organizers cited the lack of representation of women in major institutions and at major international conferences. Since that first workshop, 84 different women have participated in three WIN conferences at BIRS, with more than 60 other participants at the Women in Numbers – Europe conferences held at CIRM in Luminy and at the Lorentz Center. The number of women doing research in number theory is steadily growing. Though it is difficult to know exactly how much of this increase is due (directly or indirectly) to WIN, the visibility of the WIN conferences — due both to the community that has developed and the high quality of research output from these workshops — has helped to raise awareness in the broader community of the important contributions made by these researchers. Another major indicator of the success of the WIN conferences is the publication output: three proceed- ings volumes containing a total of 36 papers (including some survey papers), as well as more than 10 journal articles published elsewhere. This far surpasses the output of a typical research workshop or graduate focused workshop such as the Arizona Winter School. -
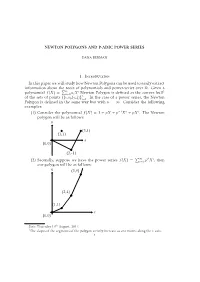
NEWTON POLYGONS and P-ADIC POWER SERIES 1. Introduction In
NEWTON POLYGONS AND P-ADIC POWER SERIES DANA BERMAN 1. Introduction In this paper we will study how Newton Polygons can be used to easily extract information about the roots of polynomials and power-series over Ω. Given a Pn i 1 polynomial f(X) = i=0 aiX Newton Polygon is defined as the convex hull n of the sets of points f(i; νp(ai))gi=1. In the case of a power series, the Newton Polygon is defined in the same way but with n = 1. Consider the following examples: (1) Consider the polynomial f(X) = 1 + pX + p−1X2 + pX3. The Newton polygon will be as follows: y (3,1) (1,1) x (0,0) (2,-1) P1 i2 i (2) Secondly, suppose we have the power series f(X) = i=0 p X , then our polygon will be as follows: y (3,9) (2,4) (1,1) x (0,0) Date: Thursday 10th August, 2017. 1The slopes of the segments of the polygon strictly increase as one moves along the x-axis. 1 2 DANA BERMAN P1 i (3) Finally, consider the power series f(X) = i=0 pX . Then notice that the associated Newton polygon is exactly the non-negative side of the x-axis. In remainder of the paper, if f(X) is a polynomial, than it will be assumed that f(X) 2 1 + Ω[X]. If f(X) is a power series, than it will be assumed that f(X) 2 1 + Ω[[X]]. Note that under these assumptions, 0 may not be a root of any polynomial or power series.