Some Aspects of Certain Form of Near Perfect Numbers
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Prime Divisors in the Rationality Condition for Odd Perfect Numbers
Aid#59330/Preprints/2019-09-10/www.mathjobs.org RFSC 04-01 Revised The Prime Divisors in the Rationality Condition for Odd Perfect Numbers Simon Davis Research Foundation of Southern California 8861 Villa La Jolla Drive #13595 La Jolla, CA 92037 Abstract. It is sufficient to prove that there is an excess of prime factors in the product of repunits with odd prime bases defined by the sum of divisors of the integer N = (4k + 4m+1 ℓ 2αi 1) i=1 qi to establish that there do not exist any odd integers with equality (4k+1)4m+2−1 between σ(N) and 2N. The existence of distinct prime divisors in the repunits 4k , 2α +1 Q q i −1 i , i = 1,...,ℓ, in σ(N) follows from a theorem on the primitive divisors of the Lucas qi−1 sequences and the square root of the product of 2(4k + 1), and the sequence of repunits will not be rational unless the primes are matched. Minimization of the number of prime divisors in σ(N) yields an infinite set of repunits of increasing magnitude or prime equations with no integer solutions. MSC: 11D61, 11K65 Keywords: prime divisors, rationality condition 1. Introduction While even perfect numbers were known to be given by 2p−1(2p − 1), for 2p − 1 prime, the universality of this result led to the the problem of characterizing any other possible types of perfect numbers. It was suggested initially by Descartes that it was not likely that odd integers could be perfect numbers [13]. After the work of de Bessy [3], Euler proved σ(N) that the condition = 2, where σ(N) = d|N d is the sum-of-divisors function, N d integer 4m+1 2α1 2αℓ restricted odd integers to have the form (4kP+ 1) q1 ...qℓ , with 4k + 1, q1,...,qℓ prime [18], and further, that there might exist no set of prime bases such that the perfect number condition was satisfied. -

Unit 6: Multiply & Divide Fractions Key Words to Know
Unit 6: Multiply & Divide Fractions Learning Targets: LT 1: Interpret a fraction as division of the numerator by the denominator (a/b = a ÷ b) LT 2: Solve word problems involving division of whole numbers leading to answers in the form of fractions or mixed numbers, e.g. by using visual fraction models or equations to represent the problem. LT 3: Apply and extend previous understanding of multiplication to multiply a fraction or whole number by a fraction. LT 4: Interpret the product (a/b) q ÷ b. LT 5: Use a visual fraction model. Conversation Starters: Key Words § How are fractions like division problems? (for to Know example: If 9 people want to shar a 50-lb *Fraction sack of rice equally by *Numerator weight, how many pounds *Denominator of rice should each *Mixed number *Improper fraction person get?) *Product § 3 pizzas at 10 slices each *Equation need to be divided by 14 *Division friends. How many pieces would each friend receive? § How can a model help us make sense of a problem? Fractions as Division Students will interpret a fraction as division of the numerator by the { denominator. } What does a fraction as division look like? How can I support this Important Steps strategy at home? - Frac&ons are another way to Practice show division. https://www.khanacademy.org/math/cc- - Fractions are equal size pieces of a fifth-grade-math/cc-5th-fractions-topic/ whole. tcc-5th-fractions-as-division/v/fractions- - The numerator becomes the as-division dividend and the denominator becomes the divisor. Quotient as a Fraction Students will solve real world problems by dividing whole numbers that have a quotient resulting in a fraction. -
![Arxiv:1412.5226V1 [Math.NT] 16 Dec 2014 Hoe 11](https://docslib.b-cdn.net/cover/0511/arxiv-1412-5226v1-math-nt-16-dec-2014-hoe-11-410511.webp)
Arxiv:1412.5226V1 [Math.NT] 16 Dec 2014 Hoe 11
q-PSEUDOPRIMALITY: A NATURAL GENERALIZATION OF STRONG PSEUDOPRIMALITY JOHN H. CASTILLO, GILBERTO GARC´IA-PULGAR´IN, AND JUAN MIGUEL VELASQUEZ-SOTO´ Abstract. In this work we present a natural generalization of strong pseudoprime to base b, which we have called q-pseudoprime to base b. It allows us to present another way to define a Midy’s number to base b (overpseudoprime to base b). Besides, we count the bases b such that N is a q-probable prime base b and those ones such that N is a Midy’s number to base b. Furthemore, we prove that there is not a concept analogous to Carmichael numbers to q-probable prime to base b as with the concept of strong pseudoprimes to base b. 1. Introduction Recently, Grau et al. [7] gave a generalization of Pocklignton’s Theorem (also known as Proth’s Theorem) and Miller-Rabin primality test, it takes as reference some works of Berrizbeitia, [1, 2], where it is presented an extension to the concept of strong pseudoprime, called ω-primes. As Grau et al. said it is right, but its application is not too good because it is needed m-th primitive roots of unity, see [7, 12]. In [7], it is defined when an integer N is a p-strong probable prime base a, for p a prime divisor of N −1 and gcd(a, N) = 1. In a reading of that paper, we discovered that if a number N is a p-strong probable prime to base 2 for each p prime divisor of N − 1, it is actually a Midy’s number or a overpseu- doprime number to base 2. -

MORE-ON-SEMIPRIMES.Pdf
MORE ON FACTORING SEMI-PRIMES In the last few years I have spent some time examining prime numbers and their properties. Among some of my new results are the a Prime Number Function F(N) and the concept of Number Fraction f(N). We can define these quantities as – (N ) N 1 f (N 2 ) 1 f (N ) and F(N ) N Nf (N 3 ) Here (N) is the divisor function of number theory. The interesting property of these functions is that when N is a prime then f(N)=0 and F(N)=1. For composite numbers f(N) is a positive fraction and F(N) will be less than one. One of the problems of major practical interest in number theory is how to rapidly factor large semi-primes N=pq, where p and q are prime numbers. This interest stems from the fact that encoded messages using public keys are vulnerable to decoding by adversaries if they can factor large semi-primes when they have a digit length of the order of 100. We want here to show how one might attempt to factor such large primes by a brute force approach using the above f(N) function. Our starting point is to consider a large semi-prime given by- N=pq with p<sqrt(N)<q By the basic definition of f(N) we get- p q p2 N f (N ) f ( pq) N pN This may be written as a quadratic in p which reads- p2 pNf (N ) N 0 It has the solution- p K K 2 N , with p N Here K=Nf(N)/2={(N)-N-1}/2. -

ON PERFECT and NEAR-PERFECT NUMBERS 1. Introduction a Perfect
ON PERFECT AND NEAR-PERFECT NUMBERS PAUL POLLACK AND VLADIMIR SHEVELEV Abstract. We call n a near-perfect number if n is the sum of all of its proper divisors, except for one of them, which we term the redundant divisor. For example, the representation 12 = 1 + 2 + 3 + 6 shows that 12 is near-perfect with redundant divisor 4. Near-perfect numbers are thus a very special class of pseudoperfect numbers, as defined by Sierpi´nski. We discuss some rules for generating near-perfect numbers similar to Euclid's rule for constructing even perfect numbers, and we obtain an upper bound of x5=6+o(1) for the number of near-perfect numbers in [1; x], as x ! 1. 1. Introduction A perfect number is a positive integer equal to the sum of its proper positive divisors. Let σ(n) denote the sum of all of the positive divisors of n. Then n is a perfect number if and only if σ(n) − n = n, that is, σ(n) = 2n. The first four perfect numbers { 6, 28, 496, and 8128 { were known to Euclid, who also succeeded in establishing the following general rule: Theorem A (Euclid). If p is a prime number for which 2p − 1 is also prime, then n = 2p−1(2p − 1) is a perfect number. It is interesting that 2000 years passed before the next important result in the theory of perfect numbers. In 1747, Euler showed that every even perfect number arises from an application of Euclid's rule: Theorem B (Euler). All even perfect numbers have the form 2p−1(2p − 1), where p and 2p − 1 are primes. -

NOTES on CARTIER and WEIL DIVISORS Recall: Definition 0.1. A
NOTES ON CARTIER AND WEIL DIVISORS AKHIL MATHEW Abstract. These are notes on divisors from Ravi Vakil's book [2] on scheme theory that I prepared for the Foundations of Algebraic Geometry seminar at Harvard. Most of it is a rewrite of chapter 15 in Vakil's book, and the originality of these notes lies in the mistakes. I learned some of this from [1] though. Recall: Definition 0.1. A line bundle on a ringed space X (e.g. a scheme) is a locally free sheaf of rank one. The group of isomorphism classes of line bundles is called the Picard group and is denoted Pic(X). Here is a standard source of line bundles. 1. The twisting sheaf 1.1. Twisting in general. Let R be a graded ring, R = R0 ⊕ R1 ⊕ ::: . We have discussed the construction of the scheme ProjR. Let us now briefly explain the following additional construction (which will be covered in more detail tomorrow). L Let M = Mn be a graded R-module. Definition 1.1. We define the sheaf Mf on ProjR as follows. On the basic open set D(f) = SpecR(f) ⊂ ProjR, we consider the sheaf associated to the R(f)-module M(f). It can be checked easily that these sheaves glue on D(f) \ D(g) = D(fg) and become a quasi-coherent sheaf Mf on ProjR. Clearly, the association M ! Mf is a functor from graded R-modules to quasi- coherent sheaves on ProjR. (For R reasonable, it is in fact essentially an equiva- lence, though we shall not need this.) We now set a bit of notation. -

The Distribution of Pseudoprimes
The Distribution of Pseudoprimes Matt Green September, 2002 The RSA crypto-system relies on the availability of very large prime num- bers. Tests for finding these large primes can be categorized as deterministic and probabilistic. Deterministic tests, such as the Sieve of Erastothenes, of- fer a 100 percent assurance that the number tested and passed as prime is actually prime. Despite their refusal to err, deterministic tests are generally not used to find large primes because they are very slow (with the exception of a recently discovered polynomial time algorithm). Probabilistic tests offer a much quicker way to find large primes with only a negligibal amount of error. I have studied a simple, and comparatively to other probabilistic tests, error prone test based on Fermat’s little theorem. Fermat’s little theorem states that if b is a natural number and n a prime then bn−1 ≡ 1 (mod n). To test a number n for primality we pick any natural number less than n and greater than 1 and first see if it is relatively prime to n. If it is, then we use this number as a base b and see if Fermat’s little theorem holds for n and b. If the theorem doesn’t hold, then we know that n is not prime. If the theorem does hold then we can accept n as prime right now, leaving a large chance that we have made an error, or we can test again with a different base. Chances improve that n is prime with every base that passes but for really big numbers it is cumbersome to test all possible bases. -

SUPERHARMONIC NUMBERS 1. Introduction If the Harmonic Mean Of
MATHEMATICS OF COMPUTATION Volume 78, Number 265, January 2009, Pages 421–429 S 0025-5718(08)02147-9 Article electronically published on September 5, 2008 SUPERHARMONIC NUMBERS GRAEME L. COHEN Abstract. Let τ(n) denote the number of positive divisors of a natural num- ber n>1andletσ(n)denotetheirsum.Thenn is superharmonic if σ(n) | nkτ(n) for some positive integer k. We deduce numerous properties of superharmonic numbers and show in particular that the set of all superhar- monic numbers is the first nontrivial example that has been given of an infinite set that contains all perfect numbers but for which it is difficult to determine whether there is an odd member. 1. Introduction If the harmonic mean of the positive divisors of a natural number n>1isan integer, then n is said to be harmonic.Equivalently,n is harmonic if σ(n) | nτ(n), where τ(n)andσ(n) denote the number of positive divisors of n and their sum, respectively. Harmonic numbers were introduced by Ore [8], and named (some 15 years later) by Pomerance [9]. Harmonic numbers are of interest in the investigation of perfect numbers (num- bers n for which σ(n)=2n), since all perfect numbers are easily shown to be harmonic. All known harmonic numbers are even. If it could be shown that there are no odd harmonic numbers, then this would solve perhaps the most longstand- ing problem in mathematics: whether or not there exists an odd perfect number. Recent articles in this area include those by Cohen and Deng [3] and Goto and Shibata [5]. -

Bound Estimation for Divisors of RSA Modulus with Small Divisor-Ratio
International Journal of Network Security, Vol.23, No.3, PP.412-425, May 2021 (DOI: 10.6633/IJNS.202105 23(3).06) 412 Bound Estimation for Divisors of RSA Modulus with Small Divisor-ratio Xingbo Wang (Corresponding author: Xingbo Wang) Department of Mechatronic Engineering, Foshan University Guangdong Engineering Center of Information Security for Intelligent Manufacturing System, China Email: [email protected]; [email protected] (Received Nov. 16, 2019; Revised and Accepted Mar. 8, 2020; First Online Apr. 17, 2021) Abstract make it easier to find the small divisor; articles [2, 10] found out the distribution of an odd integer's square-root Through subtle analysis on relationships among ances- in the T3 tree; articles [11, 15, 17] investigated divisors' tors, symmetric brothers, and the square root of a node distribution of an RSA number, presenting in detail how on the T3 tree, the article puts a method forwards to cal- two divisors distribute on the levels of the T3 tree in terms culate an interval that contains a divisor of a semiprime of their divisor-ratio. whose divisor-ratio is less than 3/2. Concrete mathemat- This paper, following the studies in [11, 15, 17], and ical reasonings to derive the method and programming based on the inequalities proved in [12] as well as the procedure from realizing the calculations are shown in theorems proved in [13, 16], gives in detail a bound esti- detail. Numerical experiments are made by applying the mation to the divisors of an RSA number. The results in method on both ordinary small semiprimes and the RSA this paper are helpful to design algorithm to search the numbers. -

Generation of Pseudoprimes Section 1:Introduction
Generation of Pseudoprimes Danielle Stewart Swenson College of Science and Engineering University of Minnesota [email protected] Section 1:Introduction: Number theory is a branch of mathematics that looks at the many properties of integers. The properties that are looked at in this paper are specifically related to pseudoprime numbers. Positive integers can be partitioned into three distinct sets. The unity, composites, and primes. It is much easier to prove that an integer is composite compared to proving primality. Fermat’s Little Theorem p If p is prime and a is any integer, then a − a is divisible by p. This theorem is commonly used to determine if an integer is composite. If a number does not pass this test, it is shown that the number must be composite. On the other hand, if a number passes this test, it does not prove this integer is prime (Anderson & Bell, 1997) . An example 5 would be to let p = 5 and let a = 2. Then 2 − 2 = 32 − 2 = 30 which is divisible by 5. Since p = 5 5 is prime, we can choose any a as a positive integer and a − a is divisible by 5. Now let p = 4 and 4 a = 2 . Then 2 − 2 = 14 which is not divisible by 4. Using this theorem, we can quickly see if a number fails, then it must be composite, but if it does not fail the test we cannot say that it is prime. This is where pseudoprimes come into play. If we know that a number n is composite but n n divides a − a for some positive integer a, we call n a pseudoprime. -
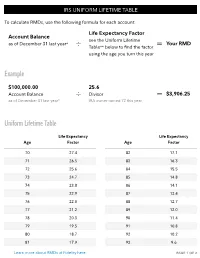
IRS Uniform Lifetime Table | Calculate Rmds | Fidelity
IRS UNIFORM LIFETIME TABLE To calculate RMDs, use the following formula for each account: Life Expectancy Factor Account Balance see the Uniform Lifetime as of December 31 last year* Your RMD ÷ Table** below to find the factor = using the age you turn this year Example $100,000.00 25.6 Account Balance ÷ Divisor = $3,906.25 as of December 31 last year* IRA owner turned 72 this year Uniform Lifetime Table Life Expectancy Life Expectancy Age Factor Age Factor 70 27.4 82 17.1 71 26.5 83 16.3 72 25.6 84 15.5 73 24.7 85 14.8 74 23.8 86 14.1 75 22.9 87 13.4 76 22.0 88 12.7 77 21.2 89 12.0 78 20.3 90 11.4 79 19.5 91 10.8 80 18.7 92 10.2 81 17.9 93 9.6 Learn more about RMDs at Fidelity here PAGE 1 OF 2 IRS UNIFORM LIFETIME TABLE Uniform Lifetime Table (continued) Life Expectancy Life Expectancy Age Factor Age Factor 94 9.1 105 4.5 95 8.6 106 4.2 96 8.1 107 3.9 97 7.6 108 3.7 98 7.1 109 3.4 99 6.7 110 3.1 100 6.3 111 2.9 101 5.9 112 2.6 102 5.5 113 2.4 103 5.2 114 2.1 104 4.9 115 and older 1.9 Learn more about RMDs at Fidelity here Source: Internal Revenue Service, Publication 590-B, Table III, Uniform Lifetime. -

Sums of Divisors, Perfect Numbers and Factoring*
J. COMPUT. 1986 Society for and Applied Mathematics No. 4, November 1986 02 SUMS OF DIVISORS, PERFECT NUMBERS AND FACTORING* ERIC GARY MILLER5 AND JEFFREY Abstract. Let N be a positive integer, and let denote the sum of the divisors of N = 1+2 +3+6 = 12). We show computing is equivalent to factoring N in the following sense: there is a random polynomial time algorithm that, given N),produces the prime factorization of N, and N) can be computed in polynomial time given the factorization of N. We show that the same result holds for the sum of the kth powers of divisors of We give three new examples of problems that are in Gill’s complexity class BPP perfect numbers, multiply perfect numbers, and amicable pairs. These are the first “natural” sets in BPP that are not obviously in RP. Key words. factoring, sum of divisors, perfect numbers, random reduction, multiply perfect numbers, amicable pairs subject classifications. 1. Introduction. Integer factoring is a well-known difficult problem whose precise computational complexity is still unknown. Several investigators have found algorithms that are much better than the classical method of trial division (see [Guy [Pol], [Dix], [Len]). We are interested in the relationship of factoring to other functions in number theory. It is trivial to show that classical functions like (the number of positive integers less than N and relatively prime to N) can be computed in polynomial time if one can factor N; hence computing is “easier” than factoring. One would also like to find functions “harder” than factoring.