Acharya Polynomial of Thorn Graphs
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Bulletin of Mathematics and Statistics Research
Vol.5.Issue.3.2017 (July-Sept) ©KY PUBLICATIONS BULLETIN OF MATHEMATICS AND STATISTICS RESEARCH A Peer Reviewed International Research Journal http://www.bomsr.com Email:[email protected] RESEARCH ARTICLE ACHARYA POLYNOMIAL OF SOME GRAPH TRANSFORMATIONS SHAILAJA S. SHIRKOL1 , SUNILKUMAR M. HOSAMANI2, SHOBHA V. PATIL3 1Department of Mathematics, SDMCET, Dharwad, Karnataka, India 2Department of Mathematics, Rani Channamma University,Belagavi, India 3Department of Mathematics KLE Dr. MSSCET, Belagavi, Karnataka India [email protected];[email protected];[email protected] ABSTRACT Let G be a connected graph of order n, the Acharya Polynomial AP(G, ) is defined as d,i xi of graph G and x is a parameter. In the present 1d n1 1i p work we determine Acharya polynomial and Acharya index of subdivision graph of wheel graph Wn and the para-line graph the wheel L(S(Wn)) for all positive integers n 3. Further we find Hosoya and Terminal Hosoya Polynomial for Kragujevac tree. Key words: Line graph, subdivision graph, para-line graph,wheel graph, Wiener index, Terminal Wiener index, Acharya index. 1. Introduction In the present paper all graphs considered are simple, finite and connected. Let G be a such graph with vertex set V(G) and edge set E(G). The number of edges incident on vertex v is called degree, d(v) of vertex. The distance between the vertices u and v is the length of shortest path. It is denoted by dG(u,v). The diameter diam(G)= p is maximum distance between two vertices of a graph G [1]. The line graph L(G) is the graph whose vertices corresponds to edges of G with two vertices being adjacent if and only if the corresponding edges in G have common vertex. -

Employees Details (1).Xlsx
Deputy Director, Animal Husbandry & Veterinary Services, Dharwad Super Specialities Hospitals ANIMAL HUSBANDRY Telephone Nos. Postal Address with PIN No. Sl. No. Name of the Officer Designation Office Fax Mobile ------- ------- ------- ------- ------- ------- Veterinary Hospitals ANIMAL HUSBANDRY Telephone Nos. Postal Address with PIN No. Sl. No. Name of the Officer Designation Office Fax Mobile Office of the Assistant Director, Veterinary 1 Dr. Jambunath Gaddi Assistant Director 0836-2443122 ------- 9448875730 Hospital, Dharwad-580008 Office of the Assistant Director, Veterinary 2 Dr. S.B.Padagannavar SVO ------- ------- 9008127745 Hospital, Alnavar-581103 Office of the Assistant Director, Veterinary 3 Dr. Tippanna SVO ------- ------- 9743285454 Hospital, Amminabhavi -581201 Office of the Assistant Director, Veterinary 4 Dr. Umesh N. Kondi Assistant Director 0836-2443415 ------- 9900675607 Hospital, Near New English School, Hubli- 580009 Office of the Assistant Director, Veterinary 5 Dr. P.B.Bankar [I/c] SVO ------- ------- 9480372315 Hospital, Byahatti-580023 Office of the Assistant Director, Veterinary 6 Dr. S.V.Santi [I/c] Assistant Director 08370-284504 ------- 9448374236 Hospital, Kalaghatagi-580114 Office of the Assistant Director, Veterinary 7 Dr. Manjunath Kurgund SVO ------- ------- 9448730137 Hospital, Dummawad-580114 Office of the Assistant Director, Veterinary 8 Dr. Mulki Patil Assistant Director 08304-290220 ------- 8310508903 Hospital, Kundgol-581113 Office of the Assistant Director, Veterinary 9 Dr. Sadanand Pattar [I/c] VO ------- ------- 9844962910 Hospital, Saunshi-581117 Office of the Assistant Director, Veterinary 10 Dr. K.H.Kyadad [I/c] Assistant Director 08380-229219 ------- 9448903324 Hospital, Navalgund-582208 Office of the Assistant Director, Veterinary 11 Dr. S.S.Patil CVO ------- ------- 9986268508 Hospital, Annigeri-582201 Office of the Assistant Director, Veterinary 12 Dr. Krishnappa R.M.[I/c] SVO ------- ------- 9449633788 Hospital, Morab-580112 Mobile Veterinary Clinics ANIMAL HUSBANDRY Telephone Nos. -

Congratulations
Vidyabharati Foundation’s INSTITUTE OF BUSINESS GROUP OF INSTITUTIONS MANAGEMENT & RESEARCH Placements for the Academic year 2019-20 Congratulations Aiswaryaprasad K. S. Akshata J. Anand N Dhongadi Anita N Gadag Nikita Shinde ICICI Bank - 3.27 L/A ICICI Bank - 3.27 L/A ICICI Bank - 3.27 L/A ICICI Bank - 3.27 L/A Akhila Soukhya-1.92 L/A Basavaraj A. Diana Anthony Gopal L. H.K. Mansurali Vidya Sayannavar ICICI Bank - 3.27 L/A Infosys - 3.68 L/A Mc Donalds - 2.57 L/A Wheels Eye - 1.89 L/A Akhila Soukhya-1.92 L/A Kavya Ankolekar Mahammadrasul F. Maheshwari B. N. Manasa V ICICI Bank - 3.27 L/A Wheels Eye - 1.94 L/A Info. Res. - 1.98 L/A Info. Res. - 1.98 L/A Wish you all the best for a successful career. Management, Director, Principal, Faculties, Staff & Students. Vidyabharati Foundation’s INSTITUTE OF BUSINESS GROUP OF INSTITUTIONS MANAGEMENT & RESEARCH Placements for the Academic year 2019-20 Congratulations Vaishnavi S. C. Mohammadusman M. M. Mujahid Kabburi Parish A Magadum Vinaya K Hasyagar Info. Res. - 1.98 L/A Pin Click - 5.52 L/A Wheels Eye - 1.89 L/A Pin Click - 5.52 L/A Info. Res. - 1.98 L/A Pooja Prashanth S. S. Sachin V Mone Sandesh Madannavar Mc Donalds - 2.57 L/A Info. Res. - 1.98 L/A Vikram M Hugar Shivaraj Bhagyad Soumya S. M. Soumyashree A. Wheels Eye - 1.89 L/A Pin Click - 5.52 L/A ICICI Bank - 3.27 L/A Direct Subzi - 1.8 L/A Wish you all the best for a successful career. -

Sub Centre List As Per HMIS SR
Sub Centre list as per HMIS SR. DISTRICT NAME SUB DISTRICT FACILITY NAME NO. 1 Bagalkote Badami ADAGAL 2 Bagalkote Badami AGASANAKOPPA 3 Bagalkote Badami ANAVALA 4 Bagalkote Badami BELUR 5 Bagalkote Badami CHOLACHAGUDDA 6 Bagalkote Badami GOVANAKOPPA 7 Bagalkote Badami HALADURA 8 Bagalkote Badami HALAKURKI 9 Bagalkote Badami HALIGERI 10 Bagalkote Badami HANAPUR SP 11 Bagalkote Badami HANGARAGI 12 Bagalkote Badami HANSANUR 13 Bagalkote Badami HEBBALLI 14 Bagalkote Badami HOOLAGERI 15 Bagalkote Badami HOSAKOTI 16 Bagalkote Badami HOSUR 17 Bagalkote Badami JALAGERI 18 Bagalkote Badami JALIHALA 19 Bagalkote Badami KAGALGOMBA 20 Bagalkote Badami KAKNUR 21 Bagalkote Badami KARADIGUDDA 22 Bagalkote Badami KATAGERI 23 Bagalkote Badami KATARAKI 24 Bagalkote Badami KELAVADI 25 Bagalkote Badami KERUR-A 26 Bagalkote Badami KERUR-B 27 Bagalkote Badami KOTIKAL 28 Bagalkote Badami KULAGERICROSS 29 Bagalkote Badami KUTAKANAKERI 30 Bagalkote Badami LAYADAGUNDI 31 Bagalkote Badami MAMATGERI 32 Bagalkote Badami MUSTIGERI 33 Bagalkote Badami MUTTALAGERI 34 Bagalkote Badami NANDIKESHWAR 35 Bagalkote Badami NARASAPURA 36 Bagalkote Badami NILAGUND 37 Bagalkote Badami NIRALAKERI 38 Bagalkote Badami PATTADKALL - A 39 Bagalkote Badami PATTADKALL - B 40 Bagalkote Badami SHIRABADAGI 41 Bagalkote Badami SULLA 42 Bagalkote Badami TOGUNSHI 43 Bagalkote Badami YANDIGERI 44 Bagalkote Badami YANKANCHI 45 Bagalkote Badami YARGOPPA SB 46 Bagalkote Bagalkot BENAKATTI 47 Bagalkote Bagalkot BENNUR Sub Centre list as per HMIS SR. DISTRICT NAME SUB DISTRICT FACILITY NAME NO. -

Prl District and Sessions Judge, Gadag RAJASHEKAR VENKANGOUDA PATIL Prl.District and Sessions Judge Cause List Date: 19-12-2020
Prl District and Sessions Judge, Gadag RAJASHEKAR VENKANGOUDA PATIL Prl.District and Sessions Judge Cause List Date: 19-12-2020 Sr. No. Case Number Timing/Next Date Party Name Advocate 02-45 to 05-45 PM 1 EX 279/2017 M/s Sundaram Finance Limitied, S.P.Patil (Refer to Lok Adalath) Chennai, Repted by Nagaraj Palankar Vs Nagaraj Ningappa Ragati 2 EX 292/2017 M/s Indusind Bank Ltd., Hubli S S Kori (Refer to Lok Adalath) Rept. by its GPA Holder, Shivashankaragouda Parwathagouda Patil Vs Vittal Premanathsa Bhandage 3 EX 36/2018 HDB Financial Services Ltd., M S Halakeri (Refer to Lok Adalath) Hubballi Rept. by its Representative Officer Vishalkumar B Doddagoudar Vs Shafasil Mohammedhafeez Khairati Mohammed Hafeez Khairathi 4 EX 37/2018 HDB Financial Services Ltd., M S Halakeri (Refer to Lok Adalath) Hubballi Rept. by its Representative Officer Vishalkumar B Doddagoudar Vs Mudassaranazar M Khairati Mohammed Hafeez Khairathi 5 EX 66/2018 M/s Sriram Transport Finance K R Naikar (Refer to Lok Adalath) Company Ltd., Gadag Rept. by its PA Holder Shankar Basappa Sutagatti Vs Raghvendra B Sathannavar 6 EX 76/2018 M/s Sriram Transport Finance K R Naikar (Refer to Lok Adalath) Company Ltd., Gadag Rept. by its PA Holder Shankar Basappa Sutagatti Vs Bharamappa Ningappa Hittalamani 7 EX 127/2018 M/s Sriram Transport Finance S B Challamarad (Refer to Lok Adalath) Company Ltd., Gadag Rept. by its PA Holder Shankar Basappa Sutagatti Vs Mohammadrafiq Mohamadhussain Dukandhur 1/5 Prl District and Sessions Judge, Gadag RAJASHEKAR VENKANGOUDA PATIL Prl.District and Sessions Judge Cause List Date: 19-12-2020 Sr. -

Land Identified for Afforestation in the Forest Limits of Dharwad District Μ
Land identified for afforestation in the forest limits of Dharwad District µ Kongavad Tadahal Arhatti Amargol Kadadhalli Kalle Kabbenur Datanal Sotakanhal Alagavadi Hebbal Naganur Hanmanhal Timmapur Harobelvadi Hanashi Javur Kallur Jirigivad Uppina Betgeri Kotbagi Byalal Shirkol Naikanur Hosatti Tadkod Sirur Ballur Halkusugal Boganur Gobbargumpi Gudisagar Lokur Shanavad Ahatti Hangarki Belavatigi Madanbhavi Pudkalkatti Gumgol Navalgund Khannur Shelvadi Morab Dubbanmardi Mugali Garag Sibargatti Kurabgatti Ag Sanhalli Bogur Hale Tegur Yadvad Kardigud Navalgund Singanhalli Mulmuttal Tali Morab Padesur Niralkatti Tegur Gulladkop Tirlapur Navalli Venkatapur Mangalgatti Imbrahimpur Timmapur Tuppadkuratti Kotur Aminbhavi Komargop Yamnur Marevad Lakmapur Durgadkeri Belur Kittur Matikop Rashrotthana Vidya Dasankop Hosval Arekurhatti Siddhapura Chilkvad Adnur Vanahalli Narendra Chandanmatti Mommigatti Kankur Kailapur Talvai Karlavad Virapur Belhar Hallikeri Kaulgeri Ramapur Yettinagudda Dharwad Kalvad Chik MalligvadHire Malligvad Hebli Hulikeri Varav Naglavi Maradgi Basapura Dindalkoppa Gongadikoppa Sasvihalli Nagarhalli Dandikoppa Somapur Govankoppa Sivalli Kambarganvi Naglavi University of Agriculture Kumbarkoppa Kamalapur Shanthinagar C olony Hebsur Ballarvad Mandihal Dharwad Kadabgatti Kogilgeri Aravatagi Sulla Behatti ANNIGERI Jaibharati Colony Kondikoppa Mugad Kiresur Amboli Honnapur Kyarkoppa Bennur Kashinhatti Alnavara Navalur Dundur Alnavar Dori Chavani Hubli Annigeri Sisvinhalli Manakapur Salkinkoppa Sattur Kalakeri Ingalahalli Dhopenhatti -
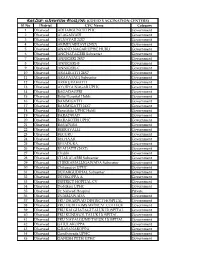
Sl No District CVC Name Category 1 Dharwad ADHARGUNCHI PHC
ಕೋ풿蓍- ಲ咾ಕರಣ ಕᲂ飍ರ ಗ쳁 (COVID VACCINATION CENTERS) Sl No District CVC Name Category 1 Dharwad ADHARGUNCHI PHC Government 2 Dharwad ALAGAWADI Government 3 Dharwad ALNAVAR 24X7 Government 4 Dharwad AMMINABHAVI (24X7) Government 5 Dharwad ANAND NAGAR UPHC HUBLI Government 6 Dharwad ANCHATAGERI Subcenter Government 7 Dharwad ANNIGERI 24X7 Government 8 Dharwad ANNIGERI-B Government 9 Dharwad ANNIGERI-C Government 10 Dharwad ARALIKATTI 24X7 Government 11 Dharwad ARAVATAGI Subcenter Government 12 Dharwad AREKURAHATTI Government 13 Dharwad AYODYA NAGAR UPHC Government 14 Dharwad BAGADAGERI Government 15 Dharwad Baliji Hospital Hubli Government 16 Dharwad BAMMIGATTI Government 17 Dharwad BAMMIGATTI 24X7 Government 18 Dharwad Banatiktta UPHC Hubli Government 19 Dharwad BARADWAD Government 20 Dharwad BARAKOTRI UPHC Government 21 Dharwad BASAPURA Government 22 Dharwad BEERAVALLI Government 23 Dharwad BEGURU Government 24 Dharwad BELHAAR Government 25 Dharwad BETADURA Government 26 Dharwad BYAHATTI (24X7) Government 27 Dharwad Chabbi Government 28 Dharwad CHAKALABBI Subcenter Government 29 Dharwad CHIKKAMALLIGAWADA Subcneter Government 30 Dharwad Chitaguppi UPHC Government 31 Dharwad DEVARGUDIHAL Subcenter Government 32 Dharwad DEVIKOPPA A Government 33 Dharwad DISTRICT HOPITAL CV Government 34 Dharwad Doddkeri UPHC Government 35 Dharwad Dr Nalwad Hospital Private 36 Dharwad DUMMAWADA Government 37 Dharwad FRU DHARWAD DISTRICT HOSPITAL Government 38 Dharwad FRU HUBLI KIMS MEDICAL COLLEGE Government 39 Dharwad FRU KALGHATAGI TALUK HOSPITAL Government -

Dr. Kishori. P. Narayankar Educational Qualification
Detailed CV Name: Dr. Kishori. P. Narayankar Educational Qualification: M.Sc.,Ph.D, P.G.D.C.A Designation: Asst Professor Address for Correspondence: Department of Mathematics Mangalore University, Mangalagangothri Mangalore-574 199 Karnataka. E-mail: [email protected] Phone: +91 8310230660 Research Areas: Graph Theory Professional Teaching Experience: 12 years Research Guidance (M.Phil. /Ph.D.): Completed students’ list (with hyperlinks to their CV if available) Registered Submitted 1. Lokesh S B : Awarded 2012-2013 February-2017 2. Shubhalakshmi D Awarded 2012-2013 October-2017 3. Dickson Selvan Awarded 2015-2016 September-2020 4. Afework Teka Submitted 2015-2016 Ongoing Registered Students’ list 5. Anteneh Alemn 2015-2016 6. Denzil Saldanha 2017-2018 7. Pandit Giri Mohandas 2017-2018 Research Projects (List)(if applicable) Completed Sl. Title of the Project Name of the Duration Status No. funding agency 1. Some Aspects of distance UGC, New Delhi 3 Years Completed Concept in Graph Theory 2. One Distance Parameters of a DST (SERB) 3 Years completed graph and its applications Ongoing: Nil Professional Collaboration(if applicable) International: Yes National Research Journal Publications (list) LIST OF PUBLICATIONS: 1. Walikar. H. B. Acharya. B. D., Kishori P. Narayankar., H. G. Shekharappa., Proc Graphs, Combinatorics, Algorithms and Applications, Edi S. Arumugam, Acharya. B. D and S. B. Rao., Narosa Publishing House. New Delhi. 2. Kishori P. Narayankar,. Lokesh S. B., Veena mathad, and Ivan Gutman, Hosoya Polynomial Of Hanoi Graphs Kragujevac Journal of Mathematics, Volume 36 Number 1 (2012), Pages 77-83. 3. Sandi KlavˇZar, Kishori P. Narayankar, H. B. Walikar Almost Self-Centered Graphs Acta Mathematica Sinica, English Series Dec., 2011, Vol. -

Society for Community Participation & Empowerment (SCOPE)
Society for Community Participation & Empowerment (SCOPE) Annual Report 2017-2018 Behind Government Primary School No.11, Betadur Compound, Malmaddi,Dharwad- 580007 Ph : 0836-2445044 E-mail: [email protected], www.scope-india.org SCOPE at a Glance Legal status: ⇒ Registered as a society under society registration act 1860 with its registration No.141/2000-2001. ⇒ Registered under section 12AA of Income Tax Act, 1961. ⇒ Registered under section 80G of IT ACT, 1961. ⇒ Registered under FCRA (Ministry of Home Affairs, Government of India), with its registration No. Social – 094520047. ⇒ PAN: AACTS 6172 R. ⇒ TAN: BLRS28625C. Vision: Enhancing quality of life of the disadvantaged communities. Mission: To facilitate community mobilisation, participation through appropriate technologies for efficient utilisation of natural resources for achieving better quality of life and value system. Objectives: ❖ To organise and empower farming community to rehabilitate tanks in an integrated manner. ❖ To enable the farmers reduce the risk of crop failure by embracing Integrated Farming System diversifying farm activities. ❖ To assist and train young professionals in the field of water and sanitation to anchor community led water and sanitation interventions at Panchayat level. ❖ To organise and mobilize farmers to set up their own entity which enables them to collectively venture into pooling, transporting, value adding and marketing their produce and thus to be self dependent and empowered. Impact so far: ● Rehabilitated 10 dilapidated irrigation tanks in Dharwad and Haveri districts of Karnataka, The structures have been maintained well. The water holding capacity of the tanks has gone up. Stored water is being used for crop cultivation. The command area which was 25% before rehabilitation rose to 75% post intervention. -

Details of Technical Experts and Farmers
Details of technical experts of UAS, Dharwad campus Sl. No. Name of the Scientist Expertise Contact No. 1. Dr. Angadi S. S. Cropping system 9449065459 2. Dr. Basavaraj Banakar Agriculture marketing 9448632398 3. Dr. M. V. Manjunatha Soil and water conservation 9449063372 4. Dr. Satish R. Desai Farm power and machineries 9448495341 5. Dr. C. B. Meti Soil and water conservation engineering 9449419613 6. Dr. Anuraj Farm power and machineries 9731907477 7. Dr. R. R. Patil Sericulture 9448894084 8. Dr. G. M. Patil Sericulture 9480461296 9. Dr. Bheemappa A. Agricultural extension 9449121372 10. Dr. S. S. Dolli Agricultural extension 9845142796 11. Dr. M. N. Sreenivasa Agriculture microbiology 9448220214 12. Dr. K. S. Jagadish Agriculture microbiology 9972755112 13. Dr. S. V. Hosmani Fodder production 9448497359 14. Dr. J. A. Mulla Poultry science 9448861650 15. Dr. S. D. Kololgi Dairy technology 9448497350 16. Dr. Ramesh Bhat Biotechnology 9945667300 17. Dr. Geeta G. Shirnalli Biogas production 9980024958 18. Dr. S. K. Deshpande Pulse breeder 9448214978 19. Dr. P. R. Dharamatti Vegetable breeder 9449070811 20. Dr. Venugopal C. K. Medicinal and aromatic plants 9448630255 21. Dr. R. V. Hegde Spices and plantation crops 9448923184 22. Dr. V. B. Nargund Mycology 9448797254 23. Dr. A. S. Byadgi Virology 9343104551 24. Dr. B. I. Bidari Soil Science & agril. chemistry 9449064306 25. Dr. Manjunath Hebbar Soil Science & agril. chemistry 9342218691 26. Dr. V. B. Kuligod Soil Science & agril. chemistry 9343167764 27. Dr. Anil Kumar Mugali Veterinary science 9845708013 28. Dr. Anil S. Patil Veterinary science 9731088592 29. Dr. Renuka S. Salunke Family resource management 9900484680 30. Dr. -
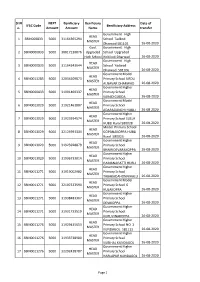
Sl.N O. IFSC Code NEFT Amount Benificiary Account Benificiary
Sl.N NEFT Benificiary Benificiary Date of IFSC Code Benificiary Address o. Amount Account Name transfer Government High HEAD 1 SBIN000833 5000 31164365294 School Tadkod MASTER Dharwad 581105 26-08-2020 Govt Government High 2 SBIN0000833 5000 36017230076 Upgraded School Upgraded High School Holtikoti Dharwad 26-08-2020 Government High HEAD 3 SBIN0000833 5000 31164343644 School Yadwad MASTER Dharwad 581206 26-08-2020 Government Model HEAD 4 SBIN0013285 5000 32034509873 Primary School URDU MASTER ALNAVAR DHARWAD 26-08-2020 Government Higher HEAD 5 SBIN0000833 5000 31991469337 Primary School MASTER KARADIGUDDA 26-08-2020 Government Model HEAD 6 SBIN0013029 5000 31921461807 Primary School MASTER ADARAGUNCHI HUBLI 26-08-2020 Government Higher HEAD 7 SBIN0013029 5000 31923914574 Primary School SULLA MASTER HUBLI Rural 580028 26-08-2020 Model Primary School HEAD 8 SBIN0013029 5000 32124991334 GOPANAKOPPA HUBLI MASTER Rural 580023 26-08-2020 Government Higher HEAD 9 SBIN0013029 5000 31925928879 Primary School MASTER BHAIRIDEVARAKOPPA 26-08-2020 Government Higher HEAD 10 SBIN0013029 5000 31936733014 Primary School MASTER GAMANAGATTI HUBLI 26-08-2020 Government Higher HEAD 11 SBIN0011271 5000 31919002982 Primary School MASTER TABAKADAHONNIHALLI 26-08-2020 Government Model HEAD 12 SBIN0011271 5000 32107333590 Primary School G MASTER HULAKOPPA 26-08-2020 Government Higher HEAD 13 SBIN0011271 5000 31938483367 Primary School MASTER DEVIKOPPA 26-08-2020 Government Higher HEAD 14 SBIN0011271 5000 31931733519 Primary School MASTER KURUVINAKOPPA 26-08-2020 Government Higher HEAD 15 SBIN0011276 5000 31929435653 Primary School NO 2 MASTER KUNDAGOL 581113 26-08-2020 Government Higher HEAD 16 SBIN0011276 5000 31933738980 Primary School MASTER KUBIHAL KUNDAGOL 26-08-2020 Government Higher HEAD 17 SBIN0011276 5000 32292418787 Primary School MASTER HARLAPUR KUNDAGOL 26-08-2020 Page 1 Sl.N NEFT Benificiary Benificiary Date of IFSC Code Benificiary Address o. -

Department of Animal Husbandry and Veterinary Services Helpline Information of Dharwad District
Department of Animal Husbandry and Veterinary Services Helpline Information of Dharwad District Name of the Hospital SL Taluk Veterinary Hospital(VH), Doctor Name Contact Number Google Links No. Name Veterinary Dispensary(VD), Primary Veterinary Centre(PVC) 1 Polyclinic Dharwad B S Lingaraju 9449541722 https://goo.gl/maps/riwvqaXu2JhXB5oD9 2 Veterinary Despensary Uppinbetegeri Sharanabasava Sajjan 9449930268 https://goo.gl/maps/qAAdHHDvDqkvzvEw6 3 Veterinary Despensary Hebbali M R Beerdar 9538912274 https://goo.gl/maps/MYGApki2tqp14YVt6 4 Veterinary Despensary Maradagi R M Krishnappa 9449633788 https://goo.gl/maps/ejJSsFL4J1QdZk7K6 5 Veterinary Despensary Tegur Ramesh Hebballi 9900470554 https://goo.gl/maps/yXM2PV6ZAWcvpxZ46 6 Veterinary Despensary Managundi Tharasing Lamani 8722891640 https://goo.gl/maps/C5BG3PJjgFbSAQoH8 7 Veterinary Despensary Narendra Prakah Bennur 9740829378 https://goo.gl/maps/4GEMgQFxi2BQyjJY7 8 Veterinary Despensary Nigadi Suresh Arakeri 6362573730 https://goo.gl/maps/o53RCAM25YdW7R3RA 9 Veterinary Despensary Navalur H R Balanggoudar 9448745923 https://goo.gl/maps/1zboP4UtnQkkK9NE7 10 Veterinary Despensary Managalgatti Anand Padeyappanavar 9449740201 https://goo.gl/maps/y1nQj5KV3nWzbK5C7 11 Veterinary Despensary Garag Ramesh Hebballi 9900470554 https://goo.gl/maps/SBUvAxYkoi7gHwu39 12 Veterinary Despensary Kotabagi Suresh Arakeri 6362573730 https://goo.gl/maps/kbR5RirFPE37ub9a8 13 Veterinary Despensary Mummigatti Aftab Yellapur 9741669450 https://goo.gl/maps/2ZUh9DYNBowHBHb87 14 Primary Veterinary Center APMC