An Introduction to Smooth Infinitesimal Analysis
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Tutorial 8: Solutions
Tutorial 8: Solutions Applications of the Derivative 1. We are asked to find the absolute maximum and minimum values of f on the given interval, and state where those values occur: (a) f(x) = 2x3 + 3x2 12x on [1; 4]. − The absolute extrema occur either at a critical point (stationary point or point of non-differentiability) or at the endpoints. The stationary points are given by f 0(x) = 0, which in this case gives 6x2 + 6x 12 = 0 = x = 1; x = 2: − ) − Checking the values at the critical points (only x = 1 is in the interval [1; 4]) and endpoints: f(1) = 7; f(4) = 128: − Therefore the absolute maximum occurs at x = 4 and is given by f(4) = 124 and the absolute minimum occurs at x = 1 and is given by f(1) = 7. − (b) f(x) = (x2 + x)2=3 on [ 2; 3] − As before, we find the critical points. The derivative is given by 2 2x + 1 f 0(x) = 3 (x2 + x)1=2 and hence we have a stationary point when 2x + 1 = 0 and points of non- differentiability whenever x2 + x = 0. Solving these, we get the three critical points, x = 1=2; and x = 0; 1: − − Checking the value of the function at these critical points and the endpoints: f( 2) = 22=3; f( 1) = 0; f( 1=2) = 2−4=3; f(0) = 0; f(3) = (12)2=3: − − − Hence the absolute minimum occurs at either x = 1 or x = 0 since in both − these cases the minimum value is 0, while the absolute maximum occurs at x = 3 and is f(3) = (12)2=3. -
Lecture Notes – 1
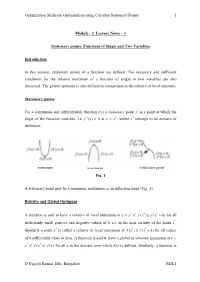
Optimization Methods: Optimization using Calculus-Stationary Points 1 Module - 2 Lecture Notes – 1 Stationary points: Functions of Single and Two Variables Introduction In this session, stationary points of a function are defined. The necessary and sufficient conditions for the relative maximum of a function of single or two variables are also discussed. The global optimum is also defined in comparison to the relative or local optimum. Stationary points For a continuous and differentiable function f(x) a stationary point x* is a point at which the slope of the function vanishes, i.e. f ’(x) = 0 at x = x*, where x* belongs to its domain of definition. minimum maximum inflection point Fig. 1 A stationary point may be a minimum, maximum or an inflection point (Fig. 1). Relative and Global Optimum A function is said to have a relative or local minimum at x = x* if f ()xfxh**≤+ ( )for all sufficiently small positive and negative values of h, i.e. in the near vicinity of the point x*. Similarly a point x* is called a relative or local maximum if f ()xfxh**≥+ ( )for all values of h sufficiently close to zero. A function is said to have a global or absolute minimum at x = x* if f ()xfx* ≤ ()for all x in the domain over which f(x) is defined. Similarly, a function is D Nagesh Kumar, IISc, Bangalore M2L1 Optimization Methods: Optimization using Calculus-Stationary Points 2 said to have a global or absolute maximum at x = x* if f ()xfx* ≥ ()for all x in the domain over which f(x) is defined. -

The Theory of Stationary Point Processes By
THE THEORY OF STATIONARY POINT PROCESSES BY FREDERICK J. BEUTLER and OSCAR A. Z. LENEMAN (1) The University of Michigan, Ann Arbor, Michigan, U.S.A. (3) Table of contents Abstract .................................... 159 1.0. Introduction and Summary ......................... 160 2.0. Stationarity properties for point processes ................... 161 2.1. Forward recurrence times and points in an interval ............. 163 2.2. Backward recurrence times and stationarity ................ 167 2.3. Equivalent stationarity conditions .................... 170 3.0. Distribution functions, moments, and sample averages of the s.p.p ......... 172 3.1. Convexity and absolute continuity .................... 172 3.2. Existence and global properties of moments ................ 174 3.3. First and second moments ........................ 176 3.4. Interval statistics and the computation of moments ............ 178 3.5. Distribution of the t n .......................... 182 3.6. An ergodic theorem ........................... 184 4.0. Classes and examples of stationary point processes ............... 185 4.1. Poisson processes ............................ 186 4.2. Periodic processes ........................... 187 4.3. Compound processes .......................... 189 4.4. The generalized skip process ....................... 189 4.5. Jitte processes ............................ 192 4.6. ~deprendent identically distributed intervals ................ 193 Acknowledgments ............................... 196 References ................................... 196 Abstract An axiomatic formulation is presented for point processes which may be interpreted as ordered sequences of points randomly located on the real line. Such concepts as forward recurrence times and number of points in intervals are defined and related in set-theoretic Q) Presently at Massachusetts Institute of Technology, Lexington, Mass., U.S.A. (2) This work was supported by the National Aeronautics and Space Administration under research grant NsG-2-59. 11 - 662901. Aeta mathematica. 116. Imprlm$ le 19 septembre 1966. -

The First Derivative and Stationary Points
Mathematics Learning Centre The first derivative and stationary points Jackie Nicholas c 2004 University of Sydney Mathematics Learning Centre, University of Sydney 1 The first derivative and stationary points dy The derivative of a function y = f(x) tell us a lot about the shape of a curve. In this dx section we will discuss the concepts of stationary points and increasing and decreasing functions. However, we will limit our discussion to functions y = f(x) which are well behaved. Certain functions cause technical difficulties so we will concentrate on those that don’t! The first derivative dy The derivative, dx ,isthe slope of the tangent to the curve y = f(x)atthe point x.Ifwe know about the derivative we can deduce a lot about the curve itself. Increasing functions dy If > 0 for all values of x in an interval I, then we know that the slope of the tangent dx to the curve is positive for all values of x in I and so the function y = f(x)isincreasing on the interval I. 3 For example, let y = x + x, then y dy 1 =3x2 +1> 0 for all values of x. dx That is, the slope of the tangent to the x curve is positive for all values of x. So, –1 0 1 y = x3 + x is an increasing function for all values of x. –1 The graph of y = x3 + x. We know that the function y = x2 is increasing for x>0. We can work this out from the derivative. 2 If y = x then y dy 2 =2x>0 for all x>0. -

EE2 Maths: Stationary Points
EE2 Maths: Stationary Points df Univariate case: When we maximize f(x) (solving for the x0 such that dx = 0) the d df gradient is zero at these points. What about the rate of change of gradient: dx ( dx ) at the minimum x0? For a minimum the gradient increases as x0 ! x0 + ∆x (∆x > 0). It follows d2f d2f that dx2 > 0. The opposite is true for a maximum: dx2 < 0, the gradient decreases upon d2f positive steps away from x0. For a point of inflection dx2 = 0. r @f @f Multivariate case: Stationary points occur when f = 0. In 2-d this is ( @x ; @y ) = 0, @f @f namely, a generalization of the univariate case. Recall that df = @x dx + @y dy can be written as df = ds · rf where ds = (dx; dy). If rf = 0 at (x0; y0) then any infinitesimal step ds away from (x0; y0) will still leave f unchanged, i.e. df = 0. There are three types of stationary points of f(x; y): Maxima, Minima and Saddle Points. We'll draw some of their properties on the board. We will now attempt to find ways of identifying the character of each of the stationary points of f(x; y). Consider a Taylor expansion about a stationary point (x0; y0). We know that rf = 0 at (x0; y0) so writing (∆x; ∆y) = (x − x0; y − y0) we find: − ∆f = f(x; y)[ f(x0; y0) ] 1 @2f @2f @2f ' 0 + (∆x)2 + 2 ∆x∆y + (∆y)2 : (1) 2! @x2 @x@y @y2 Maxima: At a maximum all small steps away from (x0; y0) lead to ∆f < 0. -

Applications of Differentiation Applications of Differentiation– a Guide for Teachers (Years 11–12)
1 Supporting Australian Mathematics Project 2 3 4 5 6 12 11 7 10 8 9 A guide for teachers – Years 11 and 12 Calculus: Module 12 Applications of differentiation Applications of differentiation – A guide for teachers (Years 11–12) Principal author: Dr Michael Evans, AMSI Peter Brown, University of NSW Associate Professor David Hunt, University of NSW Dr Daniel Mathews, Monash University Editor: Dr Jane Pitkethly, La Trobe University Illustrations and web design: Catherine Tan, Michael Shaw Full bibliographic details are available from Education Services Australia. Published by Education Services Australia PO Box 177 Carlton South Vic 3053 Australia Tel: (03) 9207 9600 Fax: (03) 9910 9800 Email: [email protected] Website: www.esa.edu.au © 2013 Education Services Australia Ltd, except where indicated otherwise. You may copy, distribute and adapt this material free of charge for non-commercial educational purposes, provided you retain all copyright notices and acknowledgements. This publication is funded by the Australian Government Department of Education, Employment and Workplace Relations. Supporting Australian Mathematics Project Australian Mathematical Sciences Institute Building 161 The University of Melbourne VIC 3010 Email: [email protected] Website: www.amsi.org.au Assumed knowledge ..................................... 4 Motivation ........................................... 4 Content ............................................. 5 Graph sketching ....................................... 5 More graph sketching .................................. -

Lecture 3: 20 September 2018 3.1 Taylor Series Approximation
COS 597G: Toward Theoretical Understanding of Deep Learning Fall 2018 Lecture 3: 20 September 2018 Lecturer: Sanjeev Arora Scribe: Abhishek Bhrushundi, Pritish Sahu, Wenjia Zhang Recall the basic form of an optimization problem: min (or max) f(x) subject to x 2 B; where B ⊆ Rd and f : Rd ! R is the objective function1. Gradient descent (ascent) and its variants are a popular choice for finding approximate solutions to these sort of problems. In fact, it turns out that these methods also work well empirically even when the objective function f is non-convex, most notably when training neural networks with various loss functions. In this lecture we will explore some of the basics ideas behind gradient descent, try to understand its limitations, and also discuss some of its popular variants that try to get around these limitations. We begin with the Taylor series approximation of functions which serves as a starting point for these methods. 3.1 Taylor series approximation We begin by recalling the Taylor series for univariate real-valued functions from Calculus 101: if f : R ! R is infinitely differentiable at x 2 R then the Taylor series for f at x is the following power series (∆x)2 (∆x)k f(x) + f 0(x)∆x + f 00(x) + ::: + f (k)(x) + ::: 2! k! Truncating this power series at some power (∆x)k results in a polynomial that approximates f around the point x. In particular, for small ∆x, (∆x)2 (∆x)k f(x + ∆x) ≈ f(x) + f 0(x)∆x + f 00(x) + ::: + f (k)(x) 2! k! Here the error of the approximation goes to zero at least as fast as (∆x)k as ∆x ! 0. -

Motion in a Straight Line Motion in a Straight Line – a Guide for Teachers (Years 11–12)
1 Supporting Australian Mathematics Project 2 3 4 5 6 12 11 7 10 8 9 A guide for teachers – Years 11 and 12 Calculus: Module 17 Motion in a straight line Motion in a straight line – A guide for teachers (Years 11–12) Principal author: Dr Michael Evans AMSI Peter Brown, University of NSW Associate Professor David Hunt, University of NSW Dr Daniel Mathews, Monash University Editor: Dr Jane Pitkethly, La Trobe University Illustrations and web design: Catherine Tan, Michael Shaw Full bibliographic details are available from Education Services Australia. Published by Education Services Australia PO Box 177 Carlton South Vic 3053 Australia Tel: (03) 9207 9600 Fax: (03) 9910 9800 Email: [email protected] Website: www.esa.edu.au © 2013 Education Services Australia Ltd, except where indicated otherwise. You may copy, distribute and adapt this material free of charge for non-commercial educational purposes, provided you retain all copyright notices and acknowledgements. This publication is funded by the Australian Government Department of Education, Employment and Workplace Relations. Supporting Australian Mathematics Project Australian Mathematical Sciences Institute Building 161 The University of Melbourne VIC 3010 Email: [email protected] Website: www.amsi.org.au Assumed knowledge ..................................... 4 Motivation ........................................... 4 Content ............................................. 6 Position, displacement and distance ........................... 6 Constant velocity ..................................... -

1 Overview 2 a Characterization of Convex Functions
AM 221: Advanced Optimization Spring 2016 Prof. Yaron Singer Lecture 8 — February 22nd 1 Overview In the previous lecture we saw characterizations of optimality in linear optimization, and we reviewed the simplex method for finding optimal solutions. In this lecture we return to convex optimization and give a characterization of optimality. The main theorem we will prove today shows that for a convex function f : S ! R defined over a convex set S, a stationary point (the point x¯ for which rf(x¯)) is a global minimum. We we will review basic definitions and properties from multivariate calculus, prove some important properties of convex functions, and obtain various characterizations of optimality. 2 A Characterization of Convex Functions Recall the definitions we introduced in the second lecture of convex sets and convex functions: Definition. A set S is called a convex set if any two points in S contain their line, i.e. for any x1; x2 2 S we have that λx1 + (1 − λ)x2 2 S for any λ 2 [0; 1]. n Definition. For a convex set S ⊆ R , we say that a function f : S ! R is convex on S if for any two points x1; x2 2 S and any λ 2 [0; 1] we have that: f (λx1 + (1 − λ)x2) ≤ λf(x1) + 1 − λ f(x2): We will first give an important characterization of convex function. To so, we need to characterize multivariate functions via their Taylor expansion. 2.1 First-order Taylor approximation n n Definition. The gradient of a function f : R ! R at point x 2 R denoted rf(x¯) is: @f(x) @f(x)| rf(x) := ;:::; @x1 @xn First-order Taylor expansion. -

Implicit Differentiation
Learning Development Service Differentiation 2 To book an appointment email: [email protected] Who is this workshop for? • Scientists-physicists, chemists, social scientists etc. • Engineers • Economists • Calculus is used almost everywhere! Learning Development Service What we covered last time : • What is differentiation? Differentiation from first principles. • Differentiating simple functions • Product and quotient rules • Chain rule • Using differentiation tables • Finding the maxima and minima of functions Learning Development Service What we will cover this time: • Second Order Differentiation • Maxima and Minima (Revisited) • Parametric Differentiation • Implicit Differentiation Learning Development Service The Chain Rule by Example (i) Differentiate : Set: The differential is then: Learning Development Service The Chain Rule: Examples Differentiate: 2 1/3 (i) y x 3x 1 (ii) y sincos x (iii) y cos3x 1 3 2x 1 (iv) y 2x 1 Learning Development Service Revisit: maxima and minima Learning Development Service Finding the maxima and minima Learning Development Service The second derivative • The second derivative is found by taking the derivative of a function twice: dy d 2 y y f (x) f (x) f (x) dx dx2 • The second derivative can be used to classify a stationary point Learning Development Service The second derivative • If x0 is the position of a stationary point, the point is a maximum if the second derivative is <0 : d 2 y 0 dx2 and a minimum if: d 2 y 0 dx2 • The nature of the stationary point is inconclusive if the second derivative=0. Learning Development Service The second derivative: Examples 3 • Find the stationary points of the function f (x) x 6x and classify the stationary points. -

Calculus Online Textbook Chapter 13 Sections 13.5 to 13.7
13.5 The Chain Rule 34 A quadratic function ax2 + by2 + cx + dy has the gradi- 42 f=x x = cos 2t y = sin 2t ents shown in Figure B. Estimate a, b, c, d and sketch two level curves. 43 f=x2-y2 x=xo+2t y=yo+3t 35 The level curves of f(x, y) are circles around (1, 1). The 44 f=xy x=t2+1 y=3 curve f = c has radius 2c. What is f? What is grad f at (0, O)? 45 f=ln xyz x = e' y = e2' = e-' 36 Suppose grad f is tangent to the hyperbolas xy = constant 46 f=2x2+3y2+z2 x=t y=t2 Z=t3 in Figure C. Draw three level curves off(x, y). Is lgrad f 1 larger 47 (a) Find df/ds and df/dt for the roller-coaster f = xy along at P or Q? Is lgrad f 1 constant along the hyperbolas? Choose the path x = cos 2t, y = sin 2t. (b) Change to f = x2 + y2 and a function that could bef: x2 + y2, x2 - y2, xy, x2y2. explain why the slope is zero. 37 Repeat Problem 36, if grad f is perpendicular to the hyper- bolas in Figure C. 48 The distance D from (x, y) to (1, 2) has D2 = (x - + (y - 2)2. Show that aD/ax = (X- l)/D and dD/ay = 38 Iff = 0, 1, 2 at the points (0, I), (1, O), (2, I), estimate grad f (y - 2)/D and [grad Dl = 1. -

Module C6 Describing Change – an Introduction to Differential Calculus 6 Table of Contents
Module C6 – Describing change – an introduction to differential calculus Module C6 Describing change – an introduction to differential calculus 6 Table of Contents Introduction .................................................................................................................... 6.1 6.1 Rate of change – the problem of the curve ............................................................ 6.2 6.2 Instantaneous rates of change and the derivative function .................................... 6.15 6.3 Shortcuts for differentiation ................................................................................... 6.19 6.3.1 Polynomial and other power functions ............................................................. 6.19 6.3.2 Exponential functions ....................................................................................... 6.28 6.3.3 Logarithmic functions ...................................................................................... 6.30 6.3.4 Trigonometric functions ................................................................................... 6.34 6.3.5 Where can’t you find a derivative of a function? ............................................. 6.37 6.4 Some applications of differential calculus ............................................................. 6.40 6.4.1 Displacement-velocity-acceleration: when derivatives are meaningful in their own right ........................................................................................................... 6.41 6.4.2 Twists and turns ...............................................................................................