More on Distributions.Pdf
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

A Matrix-Valued Bernoulli Distribution Gianfranco Lovison1 Dipartimento Di Scienze Statistiche E Matematiche “S
Journal of Multivariate Analysis 97 (2006) 1573–1585 www.elsevier.com/locate/jmva A matrix-valued Bernoulli distribution Gianfranco Lovison1 Dipartimento di Scienze Statistiche e Matematiche “S. Vianelli”, Università di Palermo Viale delle Scienze 90128 Palermo, Italy Received 17 September 2004 Available online 10 August 2005 Abstract Matrix-valued distributions are used in continuous multivariate analysis to model sample data matrices of continuous measurements; their use seems to be neglected for binary, or more generally categorical, data. In this paper we propose a matrix-valued Bernoulli distribution, based on the log- linear representation introduced by Cox [The analysis of multivariate binary data, Appl. Statist. 21 (1972) 113–120] for the Multivariate Bernoulli distribution with correlated components. © 2005 Elsevier Inc. All rights reserved. AMS 1991 subject classification: 62E05; 62Hxx Keywords: Correlated multivariate binary responses; Multivariate Bernoulli distribution; Matrix-valued distributions 1. Introduction Matrix-valued distributions are used in continuous multivariate analysis (see, for exam- ple, [10]) to model sample data matrices of continuous measurements, allowing for both variable-dependence and unit-dependence. Their potentials seem to have been neglected for binary, and more generally categorical, data. This is somewhat surprising, since the natural, elementary representation of datasets with categorical variables is precisely in the form of sample binary data matrices, through the 0-1 coding of categories. E-mail address: [email protected] URL: http://dssm.unipa.it/lovison. 1 Work supported by MIUR 60% 2000, 2001 and MIUR P.R.I.N. 2002 grants. 0047-259X/$ - see front matter © 2005 Elsevier Inc. All rights reserved. doi:10.1016/j.jmva.2005.06.008 1574 G. -

Discrete Probability Distributions Uniform Distribution Bernoulli
Discrete Probability Distributions Uniform Distribution Experiment obeys: all outcomes equally probable Random variable: outcome Probability distribution: if k is the number of possible outcomes, 1 if x is a possible outcome p(x)= k ( 0 otherwise Example: tossing a fair die (k = 6) Bernoulli Distribution Experiment obeys: (1) a single trial with two possible outcomes (success and failure) (2) P trial is successful = p Random variable: number of successful trials (zero or one) Probability distribution: p(x)= px(1 − p)n−x Mean and variance: µ = p, σ2 = p(1 − p) Example: tossing a fair coin once Binomial Distribution Experiment obeys: (1) n repeated trials (2) each trial has two possible outcomes (success and failure) (3) P ith trial is successful = p for all i (4) the trials are independent Random variable: number of successful trials n x n−x Probability distribution: b(x; n,p)= x p (1 − p) Mean and variance: µ = np, σ2 = np(1 − p) Example: tossing a fair coin n times Approximations: (1) b(x; n,p) ≈ p(x; λ = pn) if p ≪ 1, x ≪ n (Poisson approximation) (2) b(x; n,p) ≈ n(x; µ = pn,σ = np(1 − p) ) if np ≫ 1, n(1 − p) ≫ 1 (Normal approximation) p Geometric Distribution Experiment obeys: (1) indeterminate number of repeated trials (2) each trial has two possible outcomes (success and failure) (3) P ith trial is successful = p for all i (4) the trials are independent Random variable: trial number of first successful trial Probability distribution: p(x)= p(1 − p)x−1 1 2 1−p Mean and variance: µ = p , σ = p2 Example: repeated attempts to start -

STATS8: Introduction to Biostatistics 24Pt Random Variables And
STATS8: Introduction to Biostatistics Random Variables and Probability Distributions Babak Shahbaba Department of Statistics, UCI Random variables • In this lecture, we will discuss random variables and their probability distributions. • Formally, a random variable X assigns a numerical value to each possible outcome (and event) of a random phenomenon. • For instance, we can define X based on possible genotypes of a bi-allelic gene A as follows: 8 < 0 for genotype AA; X = 1 for genotype Aa; : 2 for genotype aa: • Alternatively, we can define a random, Y , variable this way: 0 for genotypes AA and aa; Y = 1 for genotype Aa: Random variables • After we define a random variable, we can find the probabilities for its possible values based on the probabilities for its underlying random phenomenon. • This way, instead of talking about the probabilities for different outcomes and events, we can talk about the probability of different values for a random variable. • For example, suppose P(AA) = 0:49, P(Aa) = 0:42, and P(aa) = 0:09. • Then, we can say that P(X = 0) = 0:49, i.e., X is equal to 0 with probability of 0.49. • Note that the total probability for the random variable is still 1. Random variables • The probability distribution of a random variable specifies its possible values (i.e., its range) and their corresponding probabilities. • For the random variable X defined based on genotypes, the probability distribution can be simply specified as follows: 8 < 0:49 for x = 0; P(X = x) = 0:42 for x = 1; : 0:09 for x = 2: Here, x denotes a specific value (i.e., 0, 1, or 2) of the random variable. -

Chapter 5 Sections
Chapter 5 Chapter 5 sections Discrete univariate distributions: 5.2 Bernoulli and Binomial distributions Just skim 5.3 Hypergeometric distributions 5.4 Poisson distributions Just skim 5.5 Negative Binomial distributions Continuous univariate distributions: 5.6 Normal distributions 5.7 Gamma distributions Just skim 5.8 Beta distributions Multivariate distributions Just skim 5.9 Multinomial distributions 5.10 Bivariate normal distributions 1 / 43 Chapter 5 5.1 Introduction Families of distributions How: Parameter and Parameter space pf /pdf and cdf - new notation: f (xj parameters ) Mean, variance and the m.g.f. (t) Features, connections to other distributions, approximation Reasoning behind a distribution Why: Natural justification for certain experiments A model for the uncertainty in an experiment All models are wrong, but some are useful – George Box 2 / 43 Chapter 5 5.2 Bernoulli and Binomial distributions Bernoulli distributions Def: Bernoulli distributions – Bernoulli(p) A r.v. X has the Bernoulli distribution with parameter p if P(X = 1) = p and P(X = 0) = 1 − p. The pf of X is px (1 − p)1−x for x = 0; 1 f (xjp) = 0 otherwise Parameter space: p 2 [0; 1] In an experiment with only two possible outcomes, “success” and “failure”, let X = number successes. Then X ∼ Bernoulli(p) where p is the probability of success. E(X) = p, Var(X) = p(1 − p) and (t) = E(etX ) = pet + (1 − p) 8 < 0 for x < 0 The cdf is F(xjp) = 1 − p for 0 ≤ x < 1 : 1 for x ≥ 1 3 / 43 Chapter 5 5.2 Bernoulli and Binomial distributions Binomial distributions Def: Binomial distributions – Binomial(n; p) A r.v. -

Lecture 6: Special Probability Distributions
The Discrete Uniform Distribution The Bernoulli Distribution The Binomial Distribution The Negative Binomial and Geometric Di Lecture 6: Special Probability Distributions Assist. Prof. Dr. Emel YAVUZ DUMAN MCB1007 Introduction to Probability and Statistics Istanbul˙ K¨ult¨ur University The Discrete Uniform Distribution The Bernoulli Distribution The Binomial Distribution The Negative Binomial and Geometric Di Outline 1 The Discrete Uniform Distribution 2 The Bernoulli Distribution 3 The Binomial Distribution 4 The Negative Binomial and Geometric Distribution The Discrete Uniform Distribution The Bernoulli Distribution The Binomial Distribution The Negative Binomial and Geometric Di Outline 1 The Discrete Uniform Distribution 2 The Bernoulli Distribution 3 The Binomial Distribution 4 The Negative Binomial and Geometric Distribution The Discrete Uniform Distribution The Bernoulli Distribution The Binomial Distribution The Negative Binomial and Geometric Di The Discrete Uniform Distribution If a random variable can take on k different values with equal probability, we say that it has a discrete uniform distribution; symbolically, Definition 1 A random variable X has a discrete uniform distribution and it is referred to as a discrete uniform random variable if and only if its probability distribution is given by 1 f (x)= for x = x , x , ··· , xk k 1 2 where xi = xj when i = j. The Discrete Uniform Distribution The Bernoulli Distribution The Binomial Distribution The Negative Binomial and Geometric Di The mean and the variance of this distribution are Mean: k k 1 x1 + x2 + ···+ xk μ = E[X ]= xi f (xi ) = xi · = , k k i=1 i=1 1/k Variance: k 2 2 2 1 σ = E[(X − μ) ]= (xi − μ) · k i=1 2 2 2 (x − μ) +(x − μ) + ···+(xk − μ) = 1 2 k The Discrete Uniform Distribution The Bernoulli Distribution The Binomial Distribution The Negative Binomial and Geometric Di In the special case where xi = i, the discrete uniform distribution 1 becomes f (x)= k for x =1, 2, ··· , k, and in this from it applies, for example, to the number of points we roll with a balanced die. -

11. Parameter Estimation
11. Parameter Estimation Chris Piech and Mehran Sahami May 2017 We have learned many different distributions for random variables and all of those distributions had parame- ters: the numbers that you provide as input when you define a random variable. So far when we were working with random variables, we either were explicitly told the values of the parameters, or, we could divine the values by understanding the process that was generating the random variables. What if we don’t know the values of the parameters and we can’t estimate them from our own expert knowl- edge? What if instead of knowing the random variables, we have a lot of examples of data generated with the same underlying distribution? In this chapter we are going to learn formal ways of estimating parameters from data. These ideas are critical for artificial intelligence. Almost all modern machine learning algorithms work like this: (1) specify a probabilistic model that has parameters. (2) Learn the value of those parameters from data. Parameters Before we dive into parameter estimation, first let’s revisit the concept of parameters. Given a model, the parameters are the numbers that yield the actual distribution. In the case of a Bernoulli random variable, the single parameter was the value p. In the case of a Uniform random variable, the parameters are the a and b values that define the min and max value. Here is a list of random variables and the corresponding parameters. From now on, we are going to use the notation q to be a vector of all the parameters: Distribution Parameters Bernoulli(p) q = p Poisson(l) q = l Uniform(a,b) q = (a;b) Normal(m;s 2) q = (m;s 2) Y = mX + b q = (m;b) In the real world often you don’t know the “true” parameters, but you get to observe data. -

Chapter 3. Discrete Random Variables and Probability Distributions
Chapter 3. Discrete random variables and probability distributions. ::::Defn: A :::::::random::::::::variable (r.v.) is a function that takes a sample point in S and maps it to it a real number. That is, a r.v. Y maps the sample space (its domain) to the real number line (its range), Y : S ! R. ::::::::Example: In an experiment, we roll two dice. Let the r.v. Y = the sum of two dice. The r.v. Y as a function: (1; 1) ! 2 (1; 2) ! 3 . (6; 6) ! 12 Discrete random variables and their distributions ::::Defn: A :::::::discrete::::::::random :::::::variable is a r.v. that takes on a ::::finite or :::::::::countably ::::::infinite number of different values. ::::Defn: The probability mass function (pmf) of a discrete r.v Y is a function that maps each possible value of Y to its probability. (It is also called the probability distribution of a discrete r.v. Y ). pY : Range(Y ) ! [0; 1]: pY (v) = P(Y = v), where ‘Y=v’ denotes the event f! : Y (!) = vg. ::::::::Notation: We use capital letters (like Y ) to denote a random variable, and a lowercase letters (like v) to denote a particular value the r.v. may take. Cumulative distribution function ::::Defn: The cumulative distribution function (cdf) is defined as F(v) = P(Y ≤ v): pY : Range(Y ) ! [0; 1]: Example: We toss two fair coins. Let Y be the number of heads. What is the pmf of Y ? What is the cdf? Quiz X a random variable. values of X: 1 3 5 7 cdf F(a): .5 .75 .9 1 What is P(X ≤ 3)? (A) .15 (B) .25 (C) .5 (D) .75 Quiz X a random variable. -

Some Discrete Distributions.Pdf
CHAPTER 6 Some discrete distributions 6.1. Examples: Bernoulli, binomial, Poisson, geometric distributions Bernoulli distribution A random variable X such that P(X = 1) = p and P(X = 0) = 1 − p is said to be a Bernoulli random variable with parameter p. Note EX = p and EX2 = p, so Var X = p − p2 = p(1 − p). We denote such a random variable by X ∼ Bern (p). Binomial distribution A random variable X has a binomial distribution with parameters n and p if P(X = n k n−k. k) = k p (1 − p) We denote such a random variable by X ∼ Binom (n; p). The number of successes in n Bernoulli trials is a binomial random variable. After some cumbersome calculations one can derive EX = np. An easier way is to realize that if X is binomial, then X = Y1 + ··· + Yn, where the Yi are independent Bernoulli variables, so . EX = EY1 + ··· + EYn = np We have not dened yet what it means for random variables to be independent, but here we mean that the events such as (Yi = 1) are independent. Proposition 6.1 Suppose , where n are independent Bernoulli random variables X := Y1 +···+Yn fYigi=1 with parameter p, then EX = np; Var X = np(1 − p): Proof. First we use the denition of expectation to see that n n X n X n X = i pi(1 − p)n−i = i pi(1 − p)n−i: E i i i=0 i=1 Then 81 82 6. SOME DISCRETE DISTRIBUTIONS n X n! X = i pi(1 − p)n−i E i!(n − i)! i=1 n X (n − 1)! = np pi−1(1 − p)(n−1)−(i−1) (i − 1)!((n − 1) − (i − 1))! i=1 n−1 X (n − 1)! = np pi(1 − p)(n−1)−i i!((n − 1) − i)! i=0 n−1 X n − 1 = np pi(1 − p)(n−1)−i = np; i i=0 where we used the Binomial Theorem (Theorem 1.1). -
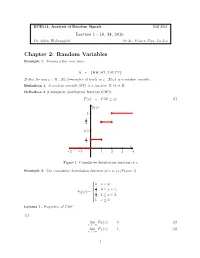
Chapter 2: Random Variables Example 1
ECE511: Analysis of Random Signals Fall 2016 Lecture 1 - 10, 24, 2016 Dr. Salim El Rouayheb Scribe: Peiwen Tian, Lu Liu Chapter 2: Random Variables Example 1. Tossing a fair coin twice: Ω = fHH;HT;TH;TT g: Define for any ! 2 Ω , X(!)=number of heads in !. X(!) is a random variable. Definition 1. A random variable (RV) is a function X: Ω ! R. Definition 2 (Cumulative distribution function(CDF)). F (χ) = P (X ≤ χ): (1) F(x) 1 3 4 0:5 1 4 x −2 −1 1 2 3 4 . Figure 1: Cumulative distribution function of x Example 2. The cumulative distribution function of x is as (Figure 1) 8 > >0 x < 0; <> 1 0 ≤ x < 1; F (x) = 4 X > 3 > 1 ≤ x < 2; :> 4 1 x ≥ 2: Lemma 1. Properties of CDF (1) lim FX (x) = 0 (2) x→−∞ lim FX (x) = 1; (3) x!+1 1 (2) FX (x) is non-decreasing: x1 ≤ x2 =) FX (x1) ≤ FX (x2) (4) (3) FX (x)is continuous from the right lim FX (x + ϵ) = FX (x); ϵ > 0 (5) ϵ!0 (4) P (a ≤ X ≤ b) = P (X ≤ b) − P (X ≤ a) + P (X = a) (6) = FX (b) − FX (a) + P (X = a) (7) (5) P (X = a) = lim FX (a) − FX (a − "); " > 0 (8) "!0 Definition 3. If random variable X has finite or countable number of values, X is called discrete. Example 3. Non-countable example:<: A set S is countable if you can find a bijection of f. f : S ! N: Definition 4. X is continuous if FX (x) is continuous. -
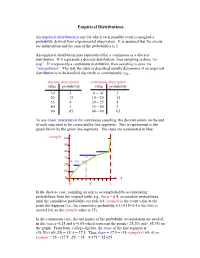
Discrete Distributions: Empirical, Bernoulli, Binomial, Poisson
Empirical Distributions An empirical distribution is one for which each possible event is assigned a probability derived from experimental observation. It is assumed that the events are independent and the sum of the probabilities is 1. An empirical distribution may represent either a continuous or a discrete distribution. If it represents a discrete distribution, then sampling is done “on step”. If it represents a continuous distribution, then sampling is done via “interpolation”. The way the table is described usually determines if an empirical distribution is to be handled discretely or continuously; e.g., discrete description continuous description value probability value probability 10 .1 0 – 10- .1 20 .15 10 – 20- .15 35 .4 20 – 35- .4 40 .3 35 – 40- .3 60 .05 40 – 60- .05 To use linear interpolation for continuous sampling, the discrete points on the end of each step need to be connected by line segments. This is represented in the graph below by the green line segments. The steps are represented in blue: rsample 60 50 40 30 20 10 0 x 0 .5 1 In the discrete case, sampling on step is accomplished by accumulating probabilities from the original table; e.g., for x = 0.4, accumulate probabilities until the cumulative probability exceeds 0.4; rsample is the event value at the point this happens (i.e., the cumulative probability 0.1+0.15+0.4 is the first to exceed 0.4, so the rsample value is 35). In the continuous case, the end points of the probability accumulation are needed, in this case x=0.25 and x=0.65 which represent the points (.25,20) and (.65,35) on the graph. -

Hand-Book on STATISTICAL DISTRIBUTIONS for Experimentalists
Internal Report SUF–PFY/96–01 Stockholm, 11 December 1996 1st revision, 31 October 1998 last modification 10 September 2007 Hand-book on STATISTICAL DISTRIBUTIONS for experimentalists by Christian Walck Particle Physics Group Fysikum University of Stockholm (e-mail: [email protected]) Contents 1 Introduction 1 1.1 Random Number Generation .............................. 1 2 Probability Density Functions 3 2.1 Introduction ........................................ 3 2.2 Moments ......................................... 3 2.2.1 Errors of Moments ................................ 4 2.3 Characteristic Function ................................. 4 2.4 Probability Generating Function ............................ 5 2.5 Cumulants ......................................... 6 2.6 Random Number Generation .............................. 7 2.6.1 Cumulative Technique .............................. 7 2.6.2 Accept-Reject technique ............................. 7 2.6.3 Composition Techniques ............................. 8 2.7 Multivariate Distributions ................................ 9 2.7.1 Multivariate Moments .............................. 9 2.7.2 Errors of Bivariate Moments .......................... 9 2.7.3 Joint Characteristic Function .......................... 10 2.7.4 Random Number Generation .......................... 11 3 Bernoulli Distribution 12 3.1 Introduction ........................................ 12 3.2 Relation to Other Distributions ............................. 12 4 Beta distribution 13 4.1 Introduction ....................................... -

Discrete Probability Distributions
Machine Learning Srihari Discrete Probability Distributions Sargur N. Srihari 1 Machine Learning Srihari Binary Variables Bernoulli, Binomial and Beta 2 Machine Learning Srihari Bernoulli Distribution • Expresses distribution of Single binary-valued random variable x ε {0,1} • Probability of x=1 is denoted by parameter µ, i.e., p(x=1|µ)=µ – Therefore p(x=0|µ)=1-µ • Probability distribution has the form Bern(x|µ)=µ x (1-µ) 1-x • Mean is shown to be E[x]=µ Jacob Bernoulli • Variance is var[x]=µ (1-µ) 1654-1705 • Likelihood of n observations independently drawn from p(x|µ) is N N x 1−x p(D | ) = p(x | ) = n (1− ) n µ ∏ n µ ∏µ µ n=1 n=1 – Log-likelihood is N N ln p(D | ) = ln p(x | ) = {x ln +(1−x )ln(1− )} µ ∑ n µ ∑ n µ n µ n=1 n=1 • Maximum likelihood estimator 1 N – obtained by setting derivative of ln p(D|µ) wrt m equal to zero is = x µML ∑ n N n=1 • If no of observations of x=1 is m then µML=m/N 3 Machine Learning Srihari Binomial Distribution • Related to Bernoulli distribution • Expresses Distribution of m – No of observations for which x=1 • It is proportional to Bern(x|µ) Histogram of Binomial for • Add up all ways of obtaining heads N=10 and ⎛ ⎞ m=0.25 ⎜ N ⎟ m N−m Bin(m | N,µ) = ⎜ ⎟µ (1− µ) ⎝⎜ m ⎠⎟ Binomial Coefficients: ⎛ ⎞ N ! ⎜ N ⎟ • Mean and Variance are ⎜ ⎟ = ⎝⎜ m ⎠⎟ m!(N −m)! N E[m] = ∑mBin(m | N,µ) = Nµ m=0 Var[m] = N (1− ) 4 µ µ Machine Learning Srihari Beta Distribution • Beta distribution a=0.1, b=0.1 a=1, b=1 Γ(a + b) Beta(µ |a,b) = µa−1(1 − µ)b−1 Γ(a)Γ(b) • Where the Gamma function is defined as ∞ Γ(x) = ∫u x−1e−u du