Information Theory
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

An Unforeseen Equivalence Between Uncertainty and Entropy
An Unforeseen Equivalence between Uncertainty and Entropy Tim Muller1 University of Nottingham [email protected] Abstract. Beta models are trust models that use a Bayesian notion of evidence. In that paradigm, evidence comes in the form of observing whether an agent has acted well or not. For Beta models, uncertainty is the inverse of the amount of evidence. Information theory, on the other hand, offers a fundamentally different approach to the issue of lacking knowledge. The entropy of a random variable is determined by the shape of its distribution, not by the evidence used to obtain it. However, we dis- cover that a specific entropy measure (EDRB) coincides with uncertainty (in the Beta model). EDRB is the expected Kullback-Leibler divergence between two Bernouilli trials with parameters randomly selected from the distribution. EDRB allows us to apply the notion of uncertainty to other distributions that may occur when generalising Beta models. Keywords: Uncertainty · Entropy · Information Theory · Beta model · Subjective Logic 1 Introduction The Beta model paradigm is a powerful formal approach to studying trust. Bayesian logic is at the core of the Beta model: \agents with high integrity be- have honestly" becomes \honest behaviour evidences high integrity". Its simplest incarnation is to apply Beta distributions naively, and this approach has limited success. However, more powerful and sophisticated approaches are widespread (e.g. [3,13,17]). A commonality among many approaches, is that more evidence (in the form of observing instances of behaviour) yields more certainty of an opinion. Uncertainty is inversely proportional to the amount of evidence. Evidence is often used in machine learning. -

Guaranteed Bounds on Information-Theoretic Measures of Univariate Mixtures Using Piecewise Log-Sum-Exp Inequalities
Preprints (www.preprints.org) | NOT PEER-REVIEWED | Posted: 20 October 2016 doi:10.20944/preprints201610.0086.v1 Peer-reviewed version available at Entropy 2016, 18, 442; doi:10.3390/e18120442 Article Guaranteed Bounds on Information-Theoretic Measures of Univariate Mixtures Using Piecewise Log-Sum-Exp Inequalities Frank Nielsen 1,2,* and Ke Sun 1 1 École Polytechnique, Palaiseau 91128, France; [email protected] 2 Sony Computer Science Laboratories Inc., Paris 75005, France * Correspondence: [email protected] Abstract: Information-theoretic measures such as the entropy, cross-entropy and the Kullback-Leibler divergence between two mixture models is a core primitive in many signal processing tasks. Since the Kullback-Leibler divergence of mixtures provably does not admit a closed-form formula, it is in practice either estimated using costly Monte-Carlo stochastic integration, approximated, or bounded using various techniques. We present a fast and generic method that builds algorithmically closed-form lower and upper bounds on the entropy, the cross-entropy and the Kullback-Leibler divergence of mixtures. We illustrate the versatile method by reporting on our experiments for approximating the Kullback-Leibler divergence between univariate exponential mixtures, Gaussian mixtures, Rayleigh mixtures, and Gamma mixtures. Keywords: information geometry; mixture models; log-sum-exp bounds 1. Introduction Mixture models are commonly used in signal processing. A typical scenario is to use mixture models [1–3] to smoothly model histograms. For example, Gaussian Mixture Models (GMMs) can be used to convert grey-valued images into binary images by building a GMM fitting the image intensity histogram and then choosing the threshold as the average of the Gaussian means [1] to binarize the image. -

A Lower Bound on the Differential Entropy of Log-Concave Random Vectors with Applications
entropy Article A Lower Bound on the Differential Entropy of Log-Concave Random Vectors with Applications Arnaud Marsiglietti 1,* and Victoria Kostina 2 1 Center for the Mathematics of Information, California Institute of Technology, Pasadena, CA 91125, USA 2 Department of Electrical Engineering, California Institute of Technology, Pasadena, CA 91125, USA; [email protected] * Correspondence: [email protected] Received: 18 January 2018; Accepted: 6 March 2018; Published: 9 March 2018 Abstract: We derive a lower bound on the differential entropy of a log-concave random variable X in terms of the p-th absolute moment of X. The new bound leads to a reverse entropy power inequality with an explicit constant, and to new bounds on the rate-distortion function and the channel capacity. Specifically, we study the rate-distortion function for log-concave sources and distortion measure ( ) = j − jr ≥ d x, xˆ x xˆ , with r 1, and we establish thatp the difference between the rate-distortion function and the Shannon lower bound is at most log( pe) ≈ 1.5 bits, independently of r and the target q pe distortion d. For mean-square error distortion, the difference is at most log( 2 ) ≈ 1 bit, regardless of d. We also provide bounds on the capacity of memoryless additive noise channels when the noise is log-concave. We show that the difference between the capacity of such channels and the capacity of q pe the Gaussian channel with the same noise power is at most log( 2 ) ≈ 1 bit. Our results generalize to the case of a random vector X with possibly dependent coordinates. -

Specific Differential Entropy Rate Estimation for Continuous-Valued Time Series
Specific Differential Entropy Rate Estimation for Continuous-Valued Time Series David Darmon1 1Department of Military and Emergency Medicine, Uniformed Services University, Bethesda, MD 20814, USA October 16, 2018 Abstract We introduce a method for quantifying the inherent unpredictability of a continuous-valued time series via an extension of the differential Shan- non entropy rate. Our extension, the specific entropy rate, quantifies the amount of predictive uncertainty associated with a specific state, rather than averaged over all states. We relate the specific entropy rate to pop- ular `complexity' measures such as Approximate and Sample Entropies. We provide a data-driven approach for estimating the specific entropy rate of an observed time series. Finally, we consider three case studies of estimating specific entropy rate from synthetic and physiological data relevant to the analysis of heart rate variability. 1 Introduction The analysis of time series resulting from complex systems must often be per- formed `blind': in many cases, mechanistic or phenomenological models are not available because of the inherent difficulty in formulating accurate models for complex systems. In this case, a typical analysis may assume that the data are the model, and attempt to generalize from the data in hand to the system. arXiv:1606.02615v1 [cs.LG] 8 Jun 2016 For example, a common question to ask about a times series is how `complex' it is, where we place complex in quotes to emphasize the lack of a satisfactory definition of complexity at present [60]. An answer is then sought that agrees with a particular intuition about what makes a system complex: for example, trajectories from periodic and entirely random systems appear simple, while tra- jectories from chaotic systems appear quite complicated. -

"Differential Entropy". In: Elements of Information Theory
Elements of Information Theory Thomas M. Cover, Joy A. Thomas Copyright 1991 John Wiley & Sons, Inc. Print ISBN 0-471-06259-6 Online ISBN 0-471-20061-1 Chapter 9 Differential Entropy We now introduce the concept of differential entropy, which is the entropy of a continuous random variable. Differential entropy is also related to the shortest description length, and is similar in many ways to the entropy of a discrete random variable. But there are some important differences, and there is need for some care in using the concept. 9.1 DEFINITIONS Definition: Let X be a random variable with cumulative distribution function F(x) = Pr(X I x). If F(x) is continuous, the random variable is said to be continuous. Let fix) = F’(x) when the derivative is defined. If J”co fb> = 1, th en fl x 1 is called the probability density function for X. The set where f(x) > 0 is called the support set of X. Definition: The differential entropy h(X) of a continuous random vari- able X with a density fix) is defined as h(X) = - f(x) log f(x) dx , (9.1) where S is the support set of the random variable. As in the discrete case, the differential entropy depends only on the probability density of the random variable, and hence the differential entropy is sometimes written as h(f) rather than h(X). 2.24 9.2 THE AEP FOR CONTZNUOUS RANDOM VARIABLES 225 Remark: As in every example involving an integral, or even a density, we should include the statement if it exists. -

January 28, 2021 1 Dealing with Infinite Universes
Information and Coding Theory Winter 2021 Lecture 6: January 28, 2021 Lecturer: Madhur Tulsiani 1 Dealing with infinite universes So far, we have only considered random variables taking values over a finite universe. We now consider how to define the various information theoretic quantities, when the set of possible values is not finite. 1.1 Countable universes When the universe is countable, various information theoretic quantities such as entropy an KL-divergence can be defined essentially as before. Of course, since we now have infinite sums in the definitions, these should be treated as limits of the appropriate series. Hence, all quantities are defined as limits of the corresponding series, when the limit exists. Convergence is usually not a problem, but it is possible to construct examples where the entropy is infinite. Consider the case of U = N, and a probability distribution P satisfying ∑x2N p(x) = 1. Since the sequence ∑x p(x) converges, usually the terms of ∑x p(x) · log(1/p(x)) are not much larger. However, we can construct an example using a the fact that ∑n≥2 1/(k · (log k) ) converges if an only if a > 1. Define C 1 1 p(x) = 8x ≥ 2 where lim = . 2 n!¥ ∑ 2 x · (log x) 2≤x≤n x · (log x) C Then, for a random variable X distributed according to P, C x · (log x)2 ( ) = · = H X ∑ 2 log ¥ . x≥2 x · (log x) C Exercise 1.1. Calculate H(X) when X be a geometric random variable with P [X = n] = (1 − p)n−1 · p 8n ≥ 1 1 1.2 Uncountable universes When the universe is not countable, one has to use measure theory to define the appropri- ate information theoretic quantities (actually, it is the KL-divergence which is defined this way). -
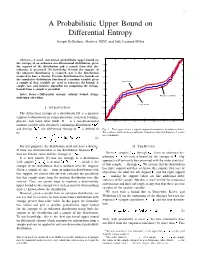
A Probabilistic Upper Bound on Differential Entropy Joseph Destefano, Member, IEEE, and Erik Learned-Miller
1 A Probabilistic Upper Bound on Differential Entropy Joseph DeStefano, Member, IEEE, and Erik Learned-Miller 1 Abstract— A novel, non-trivial, probabilistic upper bound on the entropy of an unknown one-dimensional distribution, given 0.9 the support of the distribution and a sample from that dis- tribution, is presented. No knowledge beyond the support of 0.8 the unknown distribution is required, nor is the distribution required to have a density. Previous distribution-free bounds on 0.7 the cumulative distribution function of a random variable given Upper bound a sample of that variable are used to construct the bound. A 0.6 simple, fast, and intuitive algorithm for computing the entropy bound from a sample is provided. 0.5 Index Terms— Differential entropy, entropy bound, string- 0.4 Empirical cumulative tightening algorithm 0.3 Lower bound I. INTRODUCTION 0.2 The differential entropy of a distribution [6] is a quantity 0.1 employed ubiquitously in communications, statistical learning, 0 physics, and many other fields. If is a one-dimensional 0 0.5 1 1.5 2 2.5 3 3.5 4 random variable with absolutely continuous distribution ¡£¢¥¤§¦ and density ¨©¢¥¤§¦ , the differential entropy of is defined to Fig. 1. This figure shows a typical empirical cumulative distribution (blue). The red lines show us the probabilistic bounds provided by Equation 2 on the be true cumulative. ¦ ¨©¢¥¤§¦¨©¢¤¦©¤ ¢ (1) For our purposes, the distribution need not have a density. II. THE BOUND If there are discontinuities in the distribution function ¡£¢¥¤§¦ , 1 ¤+- ¤. Given , samples, through , from an unknown dis- then no density exists and the entropy is ! . -

Chapter 5 Differential Entropy and Gaussian Channels
Chapter 5 Differential Entropy and Gaussian Channels Po-Ning Chen, Professor Institute of Communications Engineering National Chiao Tung University Hsin Chu, Taiwan 30010, R.O.C. Continuous sources I: 5-1 • Model {Xt ∈X,t∈ I} – Discrete sources ∗ Both X and I are discrete. – Continuous sources ∗ Discrete-time continuous sources ·Xis continuous; I is discrete. ∗ Waveform sources · Both X and I are continuous. • We have so far examined information measures and their operational charac- terization for discrete-time discrete-alphabet systems. In this chapter, we turn our focus to discrete-time continuous-alphabet (real-valued) sources. Information content of continuous sources I: 5-2 • If the random variable takes on values in a continuum, the minimum number of bits per symbol needed to losslessly describe it must be infinite. • This is illustrated in the following example and validated in Lemma 5.2. Example 5.1 – Consider a real-valued random variable X that is uniformly distributed on the unit interval, i.e., with pdf given by 1ifx ∈ [0, 1); fX(x)= 0otherwise. – Given a positive integer m, we can discretize X by uniformly quantizing it into m levels by partitioning the support of X into equal-length segments 1 of size ∆ = m (∆ is called the quantization step-size) such that: i i − 1 i q (X)= , if ≤ X< , m m m m for 1 ≤ i ≤ m. – Then the entropy of the quantized random variable qm(X)isgivenby m 1 1 H(q (X)) = − log2 =log2 m (in bits). m m m i=1 Information content of continuous sources I: 5-3 – Since the entropy H(qm(X)) of the quantized version of X is a lower bound to the entropy of X (as qm(X) is a function of X) and satisfies in the limit lim H(qm(X)) = lim log2 m = ∞, m→∞ m→∞ we obtain that the entropy of X is infinite. -

Entropy-Based Approach for Detecting Feature Reliability
ENTROPY-BASED APPROACH FOR DETECTING FEATURE RELIABILITY Dragoljub Pokrajac, Delaware State University [email protected] Longin Jan Latecki,Temple University [email protected] Abstract – Although a tremendous effort has been made One of the most successful approaches for motion to perform a reliable analysis of images and videos in the detection was introduced by Stauffer and Grimson [7]. It is past fifty years, the reality is that one cannot rely in 100% on based on adaptive Gaussian mixture model of the color the analysis results. In this paper, rather than proposing yet values distribution over time at each pixel location. Each another improvement in video analysis techniques, we Gaussian function in the mixture is defined by its prior discuss entropy-based monitoring of features reliability. probability, mean and a covariance matrix. In [8], we applied Major assumption of our approach is that the noise, the Stauffer-Grimson technique on spatial-temporal blocks adversingly affecting the observed feature values, is and demonstrate the robustness of the modified technique in Gaussian and that the distribution of noised feature comparison to original pixel-based approach. approaches the normal distribution with higher magnitudes of noise. In this paper, we consider one-dimensional features In [9] we have shown that the motion detection algorithms and compare two different ways of differential entropy based on local variation are not only a much simpler but also estimation—histogram based and the parametric based can be a more adequate model for motion detection for estimation. We demonstrate that the parametric approach is infrared videos. This technique can significantly reduce the superior and applicable to identify time intervals of a test processing time in comparison to the Gaussian mixture video where the observed features are not reliable for motion model, due to smaller complexity of the local variation detection tasks. -

Measuring the Complexity of Continuous Distributions
Entropy 2015, xx, 1-x; doi:10.3390/—— OPEN ACCESS entropy ISSN 1099-4300 www.mdpi.com/journal/entropy Article Measuring the Complexity of Continuous Distributions Guillermo Santamaría-Bonfil 1;2*, Nelson Fernández 3;4* and Carlos Gershenson 1;2;5;6;7* 1Instituto de Investigaciones en Matemáticas Aplicadas y en Sistemas, Universidad Nacional Autónoma de México. 2 Centro de Ciencias de la Complejidad, UNAM, México. 3 Laboratorio de Hidroinformática, Universidad de Pamplona, Colombia. 4 Grupo de Investigación en Ecología y Biogeografía, Universidad de Pamplona, Colombia. 5 SENSEable City Lab, Massachusetts Institute of Technology, USA. 6 MoBS Lab, Northeastern University, USA. 7 ITMO University, St. Petersburg, Russian Federation. * Authors to whom correspondence should be addressed; [email protected], [email protected],[email protected]. Received: xx / Accepted: xx / Published: xx Abstract: We extend previously proposed measures of complexity, emergence, and self-organization to continuous distributions using differential entropy. This allows us to calculate the complexity of phenomena for which distributions are known. We find that a broad range of common parameters found in Gaussian and scale-free distributions present high complexity values. We also explore the relationship between our measure of complexity and information adaptation. Keywords: complexity; emergence; self-organization; information; differential entropy; arXiv:1511.00529v1 [nlin.AO] 2 Nov 2015 probability distributions. 1. Introduction We all agree that complexity is everywhere. Yet, there is no agreed definition of complexity. Perhaps complexity is so general that it resists definition [1]. Still, it is useful to have formal measures of complexity to study and compare different phenomena [2]. -

Undersmoothed Kernel Entropy Estimators MAIN RESULTS
1 Undersmoothed kernel entropy estimators MAIN RESULTS We assume that data {xj }, 1 ≤ j ≤ N, are drawn i.i.d. from some Liam Paninski and Masanao Yajima arbitrary probability measure p. We are interested in estimating the Department of Statistics, Columbia University differential entropy of p (Cover and Thomas, 1991), [email protected], [email protected] dp(s) dp(s) http://www.stat.columbia.edu/∼liam H(p) = − log ds ds ds Z (for clarity, we will restrict our attention here to the case that the base Abstract— We develop a “plug-in” kernel estimator for the differential measure ds is Lebesgue measure on a finite one-dimensional interval entropy that is consistent even if the kernel width tends to zero as quickly X of length µ(X ), though extensions of the following results to more as 1/N, where N is the number of i.i.d. samples. Thus, accurate density general measure spaces are possible.) estimates are not required for accurate kernel entropy estimates; in fact, it is a good idea when estimating entropy to sacrifice some accuracy in We will consider kernel entropy estimators of the following form: the quality of the corresponding density estimate. Hˆ = g(ˆp(s))ds, Index Terms— Approximation theory, bias, consistency, distribution- free bounds, density estimation. Z where we define the kernel density estimate N 1 pˆ(s) = k(s − xj ), N INTRODUCTION j=1 X The estimation of the entropy and of related quantities (mutual with k(.) the kernel; as usual, kds = 1 and k ≥ 0. The standard information, Kullback-Leibler divergence, etc.) from i.i.d. -

On Relations Between the Relative Entropy and Χ2-Divergence, Generalizations and Applications
entropy Article On Relations Between the Relative Entropy and c2-Divergence, Generalizations and Applications Tomohiro Nishiyama 1 and Igal Sason 2,* 1 Independent Researcher, Tokyo 206–0003, Japan; [email protected] 2 Faculty of Electrical Engineering, Technion—Israel Institute of Technology, Technion City, Haifa 3200003, Israel * Correspondence: [email protected]; Tel.: +972-4-8294699 Received: 22 April 2020; Accepted: 17 May 2020; Published: 18 May 2020 Abstract: The relative entropy and the chi-squared divergence are fundamental divergence measures in information theory and statistics. This paper is focused on a study of integral relations between the two divergences, the implications of these relations, their information-theoretic applications, and some generalizations pertaining to the rich class of f -divergences. Applications that are studied in this paper refer to lossless compression, the method of types and large deviations, strong data–processing inequalities, bounds on contraction coefficients and maximal correlation, and the convergence rate to stationarity of a type of discrete-time Markov chains. Keywords: relative entropy; chi-squared divergence; f -divergences; method of types; large deviations; strong data–processing inequalities; information contraction; maximal correlation; Markov chains 1. Introduction The relative entropy (also known as the Kullback–Leibler divergence [1]) and the chi-squared divergence [2] are divergence measures which play a key role in information theory, statistics, learning, signal processing, and other theoretical and applied branches of mathematics. These divergence measures are fundamental in problems pertaining to source and channel coding, combinatorics and large deviations theory, goodness-of-fit and independence tests in statistics, expectation–maximization iterative algorithms for estimating a distribution from an incomplete data, and other sorts of problems (the reader is referred to the tutorial paper by Csiszár and Shields [3]).