DOCSLIB.ORG

MOSEK Fusion API for Java Release 9.3.6

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
MOSEK Fusion API for Java Release 9.3.6 MOSEK Fusion API for Java Release 9.3.6 MOSEK ApS 07 September 2021 Contents 1 Introduction 1 1.1 Why the Fusion API for Java?.................................2 2 Contact Information 3 3 License Agreement 4 4 Installation 8 4.1 Building Examples and Testing the Installation........................9 5 Design Overview 11 6 Conic Modeling 13 6.1 The model............................................ 13 6.2 Variables............................................. 14 6.3 Linear algebra.......................................... 14 6.4 Constraints and objective.................................... 15 6.5 Matrices............................................. 16 6.6 Parameters............................................ 17 6.7 Stacking and views....................................... 17 6.8 Vectorization........................................... 18 6.9 Reoptimization.......................................... 19 7 Optimization Tutorials 20 7.1 Linear Optimization....................................... 20 7.2 Conic Quadratic Optimization................................. 22 7.3 Power Cone Optimization.................................... 26 7.4 Conic Exponential Optimization................................ 28 7.5 Semidefinite Optimization.................................... 31 7.6 Integer Optimization...................................... 36 7.7 Geometric Programming.................................... 39 7.8 Library of basic functions.................................... 42 7.9 Model Parametrization and Reoptimization.......................... 47 7.10 Problem Modification and Reoptimization.......................... 50 8 Solver Interaction Tutorials 54 8.1 Accessing the solution...................................... 54 8.2 Errors and exceptions...................................... 58 8.3 Input/Output.......................................... 60 8.4 Setting solver parameters.................................... 61 8.5 Retrieving information items.................................. 62 8.6 Stopping the solver....................................... 63 8.7 Progress and data callback................................... 64 8.8 Optimizer API Task....................................... 67 8.9 MOSEK OptServer....................................... 67 9 Debugging Tutorials 69 9.1 Understanding optimizer log.................................. 69 i 9.2 Addressing numerical issues................................... 74 9.3 Debugging infeasibility..................................... 76 9.4 Python Console......................................... 80 10 Technical guidelines 83 10.1 Limitations............................................ 83 10.2 Memory management and garbage collection......................... 83 10.3 Names.............................................. 84 10.4 Multithreading.......................................... 85 10.5 Efficiency............................................. 85 10.6 The license system........................................ 87 10.7 Deployment........................................... 87 11 Case Studies 88 11.1 Portfolio Optimization..................................... 89 11.2 Primal Support-Vector Machine (SVM)............................ 101 11.3 2D Total Variation........................................ 105 11.4 Multiprocessor Scheduling................................... 110 11.5 Logistic regression........................................ 114 11.6 Inner and outer Löwner-John Ellipsoids............................ 116 11.7 SUDOKU............................................. 120 11.8 Travelling Salesman Problem (TSP).............................. 125 11.9 Nearest Correlation Matrix Problem.............................. 129 11.10 Semidefinite Relaxation of MIQCQO Problems........................ 133 12 Problem Formulation and Solutions 137 12.1 Linear Optimization....................................... 137 12.2 Conic Optimization....................................... 140 12.3 Semidefinite Optimization.................................... 144 13 Optimizers 146 13.1 Presolve.............................................. 146 13.2 Linear Optimization....................................... 148 13.3 Conic Optimization - Interior-point optimizer......................... 155 13.4 The Optimizer for Mixed-integer Problems.......................... 159 14 Fusion API Reference 163 14.1 Fusion API conventions..................................... 163 14.2 Class list............................................. 164 14.3 Parameters grouped by topic.................................. 244 14.4 Parameters (alphabetical list sorted by type)......................... 252 14.5 Enumerations.......................................... 278 14.6 Constants............................................. 279 14.7 Exceptions............................................ 302 14.8 Class LinAlg........................................... 306 15 Supported File Formats 311 15.1 The LP File Format....................................... 312 15.2 The MPS File Format...................................... 317 15.3 The OPF Format........................................ 329 15.4 The CBF Format........................................ 339 15.5 The PTF Format........................................ 353 15.6 The Task Format........................................ 358 15.7 The JSON Format........................................ 358 15.8 The Solution File Format.................................... 366 16 List of examples 369 17 Interface changes 371 ii 17.1 Backwards compatibility.................................... 371 17.2 Parameters............................................ 372 17.3 Constants............................................. 373 Bibliography 374 Symbol Index 375 Index 378 iii Chapter 1 Introduction The MOSEK Optimization Suite 9.3.6 is a powerful software package capable of solving large-scale optimization problems of the following kind: • linear, • conic: – conic quadratic (also known as second-order cone), – involving the exponential cone, – involving the power cone, – semidefinite, • convex quadratic and quadratically constrained, • integer. In order to obtain an overview of features in the MOSEK Optimization Suite consult the product introduction guide. The most widespread class of optimization problems is linear optimization problems, where all rela- tions are linear. The tremendous success of both applications and theory of linear optimization can be ascribed to the following factors: • The required data are simple, i.e. just matrices and vectors. • Convexity is guaranteed since the problem is convex by construction. • Linear functions are trivially differentiable. • There exist very efficient algorithms and software for solving linear problems. • Duality properties for linear optimization are nice and simple. Even if the linear optimization model is only an approximation to the true problem at hand, the advantages of linear optimization may outweigh the disadvantages. In some cases, however, the problem formulation is inherently nonlinear and a linear approximation is either intractable or inadequate. Conic optimization has proved to be a very expressive and powerful way to introduce nonlinearities, while preserving all the nice properties of linear optimization listed above. The fundamental expression in linear optimization is a linear expression of the form Ax − b ≥ 0: In conic optimization this is replaced with a wider class of constraints Ax − b 2 K where K is a convex cone. For example in 3 dimensions K may correspond to an ice cream cone. The conic optimizer in MOSEK supports a number of different types of cones K, which allows a surprisingly large number of nonlinear relations to be modeled, as described in the MOSEK Modeling Cookbook, while preserving the nice algorithmic and theoretical properties of linear optimization. 1 1.1 Why the Fusion API for Java? Fusion is an object oriented API specifically designed to build conic optimization models in a simple and expressive manner, using mainstream programming languages. With focus on usability and compactness, it helps the user focus on modeling instead of coding. Typically a conic optimization model in Fusion can be developed in a fraction of the time compared to using a low-level C API, but of course Fusion introduces a computational overhead compared to customized C code. In most cases, however, the overhead is small compared to the overall solution time. Moreover, parametrization makes it possible to construct a Fusion model once and then solve it repeatedly for different inputs with almost no overhead. We generally recommend that Fusion is used as a first step for building and verifying new models. Often, the final Fusion implementation will be directly suited for production code, and otherwise it readily provides a reference implementation for model verification. Fusion always yields readable and easily portable code. The Fusion API for Java provides access to Conic Optimization, including: • Linear Optimization (LO) • Conic Quadratic (Second-Order Cone) Optimization (CQO, SOCO) • Power Cone Optimization • Conic Exponential Optimization (CEO) • Semidefinite Optimization (SDO) • Mixed-Integer Optimization (MIO) as well as to an auxiliary linear algebra library. Convex Quadratic and Quadratically Constrained (QCQO) problems can be reformulated as Conic Quadratic problems and subsequently solved using Fusion. This is the recommended approach, as described in the MOSEK Modeling Cookbook and this whitepaper. 2 Chapter 2 Contact Information Phone +45 7174 9373 Website mosek.com Email [email protected]
Load more

Recommended publications
  • Chapter 5 Names, Bindings, and Scopes
    Chapter 5 Names, Bindings, and Scopes 5.1 Introduction 198 5.2 Names 199 5.3 Variables 200 5.4 The Concept of Binding 203 5.5 Scope 211 5.6 Scope and Lifetime 222 5.7 Referencing Environments 223 5.8 Named Constants 224 Summary • Review Questions • Problem Set • Programming Exercises 227 CMPS401 Class Notes (Chap05) Page 1 / 20 Dr. Kuo-pao Yang Chapter 5 Names, Bindings, and Scopes 5.1 Introduction 198 Imperative languages are abstractions of von Neumann architecture – Memory: stores both instructions and data – Processor: provides operations for modifying the contents of memory Variables are characterized by a collection of properties or attributes – The most important of which is type, a fundamental concept in programming languages – To design a type, must consider scope, lifetime, type checking, initialization, and type compatibility 5.2 Names 199 5.2.1 Design issues The following are the primary design issues for names: – Maximum length? – Are names case sensitive? – Are special words reserved words or keywords? 5.2.2 Name Forms A name is a string of characters used to identify some entity in a program. Length – If too short, they cannot be connotative – Language examples: . FORTRAN I: maximum 6 . COBOL: maximum 30 . C99: no limit but only the first 63 are significant; also, external names are limited to a maximum of 31 . C# and Java: no limit, and all characters are significant . C++: no limit, but implementers often impose a length limitation because they do not want the symbol table in which identifiers are stored during compilation to be too large and also to simplify the maintenance of that table.
    [Show full text]
  • Gotcha Again More Subtleties in the Verilog and Systemverilog Standards That Every Engineer Should Know
    Gotcha Again More Subtleties in the Verilog and SystemVerilog Standards That Every Engineer Should Know Stuart Sutherland Sutherland HDL, Inc. [email protected] Don Mills LCDM Engineering [email protected] Chris Spear Synopsys, Inc. [email protected] ABSTRACT The definition of gotcha is: “A misfeature of....a programming language...that tends to breed bugs or mistakes because it is both enticingly easy to invoke and completely unexpected and/or unreasonable in its outcome. A classic gotcha in C is the fact that ‘if (a=b) {code;}’ is syntactically valid and sometimes even correct. It puts the value of b into a and then executes code if a is non-zero. What the programmer probably meant was ‘if (a==b) {code;}’, which executes code if a and b are equal.” (http://www.hyperdictionary.com/computing/gotcha). This paper documents 38 gotchas when using the Verilog and SystemVerilog languages. Some of these gotchas are obvious, and some are very subtle. The goal of this paper is to reveal many of the mysteries of Verilog and SystemVerilog, and help engineers understand the important underlying rules of the Verilog and SystemVerilog languages. The paper is a continuation of a paper entitled “Standard Gotchas: Subtleties in the Verilog and SystemVerilog Standards That Every Engineer Should Know” that was presented at the Boston 2006 SNUG conference [1]. SNUG San Jose 2007 1 More Gotchas in Verilog and SystemVerilog Table of Contents 1.0 Introduction ............................................................................................................................3 2.0 Design modeling gotchas .......................................................................................................4 2.1 Overlapped decision statements ................................................................................... 4 2.2 Inappropriate use of unique case statements ...............................................................
    [Show full text]
  • Advanced Practical Programming for Scientists
    Advanced practical Programming for Scientists Thorsten Koch Zuse Institute Berlin TU Berlin SS2017 The Zen of Python, by Tim Peters (part 1) ▶︎ Beautiful is better than ugly. ▶︎ Explicit is better than implicit. ▶︎ Simple is better than complex. ▶︎ Complex is better than complicated. ▶︎ Flat is better than nested. ▶︎ Sparse is better than dense. ▶︎ Readability counts. ▶︎ Special cases aren't special enough to break the rules. ▶︎ Although practicality beats purity. ▶︎ Errors should never pass silently. ▶︎ Unless explicitly silenced. ▶︎ In the face of ambiguity, refuse the temptation to guess. Advanced Programming 78 Ex1 again • Remember: store the data and compute the geometric mean on this stored data. • If it is not obvious how to compile your program, add a REAME file or a comment at the beginning • It should run as ex1 filenname • If you need to start something (python, python3, ...) provide an executable script named ex1 which calls your program, e.g. #/bin/bash python3 ex1.py $1 • Compare the number of valid values. If you have a lower number, you are missing something. If you have a higher number, send me the wrong line I am missing. File: ex1-100.dat with 100001235 lines Valid values Loc0: 50004466 with GeoMean: 36.781736 Valid values Loc1: 49994581 with GeoMean: 36.782583 Advanced Programming 79 Exercise 1: File Format (more detail) Each line should consists of • a sequence-number, • a location (1 or 2), and • a floating point value > 0. Empty lines are allowed. Comments can start a ”#”. Anything including and after “#” on a line should be ignored.
    [Show full text]
  • Systemverilog Testbench Constructs VCS®/Vcsi™Version X-2005.06 LCA August 2005
    SystemVerilog Testbench Constructs VCS®/VCSi™Version X-2005.06 LCA August 2005 The SystemVerilog features of the Native Testbench technology in VCS documented here are currently available to customers as a part of an Limited Access program. Using these features requires additional LCA license features. Please contact you local Synopsys AC for more details. Comments? E-mail your comments about this manual to [email protected]. Copyright Notice and Proprietary Information Copyright 2005 Synopsys, Inc. All rights reserved. This software and documentation contain confidential and proprietary information that is the property of Synopsys, Inc. The software and documentation are furnished under a license agreement and may be used or copied only in accordance with the terms of the license agreement. No part of the software and documentation may be reproduced, transmitted, or translated, in any form or by any means, electronic, mechanical, manual, optical, or otherwise, without prior written permission of Synopsys, Inc., or as expressly provided by the license agreement. Destination Control Statement All technical data contained in this publication is subject to the export control laws of the United States of America. Disclosure to nationals of other countries contrary to United States law is prohibited. It is the reader’s responsibility to determine the applicable regulations and to comply with them. Disclaimer SYNOPSYS, INC., AND ITS LICENSORS MAKE NO WARRANTY OF ANY KIND, EXPRESS OR IMPLIED, WITH REGARD TO THIS MATERIAL, INCLUDING,
    [Show full text]
  • Software II: Principles of Programming Languages Introduction
    Software II: Principles of Programming Languages Lecture 5 – Names, Bindings, and Scopes Introduction • Imperative languages are abstractions of von Neumann architecture – Memory – Processor • Variables are characterized by attributes – To design a type, must consider scope, lifetime, type checking, initialization, and type compatibility Names • Design issues for names: – Are names case sensitive? – Are special words reserved words or keywords? Names (continued) • Length – If too short, they cannot be connotative – Language examples: • FORTRAN 95: maximum of 31 (only 6 in FORTRAN IV) • C99: no limit but only the first 63 are significant; also, external names are limited to a maximum of 31 (only 8 are significant K&R C ) • C#, Ada, and Java: no limit, and all are significant • C++: no limit, but implementers often impose one Names (continued) • Special characters – PHP: all variable names must begin with dollar signs – Perl: all variable names begin with special characters, which specify the variable’s type – Ruby: variable names that begin with @ are instance variables; those that begin with @@ are class variables Names (continued) • Case sensitivity – Disadvantage: readability (names that look alike are different) • Names in the C-based languages are case sensitive • Names in others are not • Worse in C++, Java, and C# because predefined names are mixed case (e.g. IndexOutOfBoundsException ) Names (continued) • Special words – An aid to readability; used to delimit or separate statement clauses • A keyword is a word that is special only
    [Show full text]
  • Systemverilog 3.1A Language Reference Manual
    Accellera SystemVerilog 3.1a Extensions to Verilog-2001 Section 17 Assertions 17.1 Introduction (informative) SystemVerilog adds features to specify assertions of a system. An assertion specifies a behavior of the system. Assertions are primarily used to validate the behavior of a design. In addition, assertions can be used to pro- vide functional coverage and generate input stimulus for validation. There are two kinds of assertions: concurrent and immediate. — Immediate assertions follow simulation event semantics for their execution and are executed like a state- ment in a procedural block. Immediate assertions are primarily intended to be used with simulation. — Concurrent assertions are based on clock semantics and use sampled values of variables. One of the goals of SystemVerilog assertions is to provide a common semantic meaning for assertions so that they can be used to drive various design and verification tools. Many tools, such as formal verification tools, evaluate circuit descriptions using cycle-based semantics, which typically relies on a clock signal or signals to drive the evaluation of the circuit. Any timing or event behavior between clock edges is abstracted away. Con- current assertions incorporate these clock semantics. While this approach generally simplifies the evalua- tion of a circuit description, there are a number of scenarios under which this cycle-based evaluation provides different behavior from the standard event-based evaluation of SystemVerilog. This section describes both types of assertions. 17.2 Immediate assertions The immediate assertion statement is a test of an expression performed when the statement is executed in the procedural code. The expression is non-temporal and is interpreted the same way as an expression in the con- dition of a procedural if statement.
    [Show full text]
  • Static Variable. • How Else Can You Affect the Rotation of Bumpers? – After the Ball Strikes a Rotation Wall, the Rotation of an Individual Bumper Changes
    Java Puzzle Ball Nick Ristuccia Lesson 2-2 Static vs Instance Variables Copyright © 2017, Oracle and/or its affiliates. All rights reserved. | One Quick Note • In this lesson, we'll be using the term variable. • Like a variable in mathematics, a Java variable represents a value. • Fields utilize variables: – In Lab 1, the variable balance represents the amount of money in an account. – The value of balance may change. – There are different ways fields can utilize variables. We'll explore this in this lesson. public class SavingsAccount { //Fields private String accountType; private String accountOwner; private double balance; private double interestRate; … } Variables Copyright © 2017, Oracle and/or its affiliates. All rights reserved. | 3 Exercise 2 • Play Basic Puzzles 8 through 11. • Consider the following: – What happens when you rotate the BlueWheel? – How else can you affect the rotation of bumpers? Copyright © 2017, Oracle and/or its affiliates. All rights reserved. | 4 Java Puzzle Ball Debriefing • What happens when you rotate the BlueWheel? – The orientation of all BlueBumpers change. – All BlueBumpers share the orientation property. – Orientation can be represented by a static variable. • How else can you affect the rotation of bumpers? – After the ball strikes a rotation wall, the rotation of an individual bumper changes. – Rotation can be represented by an instance variable. Rotation wall Copyright © 2017, Oracle and/or its affiliates. All rights reserved. | 5 Static Variable: Orientation • This static variable is shared by all instances. • Static variables apply to the class, not to any individual instance. • Therefore, a static variable needs to be changed only once for every instance to be affected.
    [Show full text]
  • From What I Have Learned About Global and Static Variables, If a C Variable Is Declared Outside All Functions in a Source File As: Int A;
    From what I have learned about global and static variables, If a C variable is declared outside all functions in a source file as: int a; This variable can be accessed by other files once it has an extern declaration for it in that file. But if the same variable is declared as: static int a; then this variable can be used only by the current file, any other file wont be able to see this variable. 1. When the program is loaded into the memory at run time, both Global and static variable are present in the Data section of this program. I want to understand that as both are stored in the same memory segment, how is the static variable protected from not getting used in any instruction out of its scope. What I think is that the scope of the variable and its access will be taken care of by the compiler. Please comment if I am wrong and add if I am missing any detail. 2. Regarding Extern variable. If, int a; is defined in file file1.c and is declared in file file2.c as: extern int a; both files belongs to different processes, let it be process1 and process2 respectively. So when process1 is running and its address space is loaded in the memory its data section variable "a" will be available. I have a doubt here, that is, when process2 is running will this variable also be loaded in process2's data section? or how it is managed. Please help me clear my above mentioned doubts.
    [Show full text]
  • Chapter 5 Variables Names Address Types Variables Assignment Binding Lifetime Scope Constants
    Topics Imperative Paradigm Chapter 5 Variables Names Address Types Variables Assignment Binding Lifetime Scope Constants Chapter 5: Variables 2 Imperative Paradigm Von Neumann Architecture The most widely used and well-developed programming paradigm. The architecture of the von Neumann Emerged alongside the first computers and machine has a memory, which computer programs in the 1940s. contains both program instructions and Its elements directly mirror the architectural data values, and a processor, which characteristics of most modern computers provides operations for modifying the This chapter discusses the key programming contents of the memory. language features that support the imperative paradigm. Chapter 5: Variables 3 Chapter 5: Variables 4 Programming Language: Turing Von Neumann Architecture Complete Turing complete: contains integer variables, values, and operations, assignment statements and the control, constructs of statement sequencing, conditionals, and branching statements. n Other statement forms (while and for loops, case selections, procedure declarations and calls, etc) and data types (strings, floating point values, etc) are provided in modern languages only to enhance the ease of programming various complex applications. Chapter 5: Variables 5 Chapter 5: Variables 6 1 Imperative Programming Variables Language Turing complete A variable is an abstraction of a memory Also supports a number of additional cell or collection of cells. fundamental features: n Integer variables are very close to the n Data types for real numbers, characters, strings, Booleans and their operands. characteristics of the memory cells: n Control structures, for and while loops, case (switch) represented as an individual hardware statements. memory word. n Arrays and element assignment. n A 3-D array is less related to the organization n Record structures and element assignment.
    [Show full text]
  • Optimization Techniques for Memory Virtualization-Based Resource Management
    SSStttooonnnyyy BBBrrrooooookkk UUUnnniiivvveeerrrsssiiitttyyy The official electronic file of this thesis or dissertation is maintained by the University Libraries on behalf of The Graduate School at Stony Brook University. ©©© AAAllllll RRRiiiggghhhtttsss RRReeessseeerrrvvveeeddd bbbyyy AAAuuuttthhhooorrr... Optimization Techniques for Memory Virtualization-based Resource Management A Dissertation Presented by Jui-Hao Chiang to The Graduate School in Partial Fulfillment of the Requirements for the Degree of Doctor of Philosophy in Computer Science Stony Brook University December 2012 Stony Brook University The Graduate School Jui-Hao Chiang We, the dissertation committee for the above candidate for the Doctor of Philosophy degree, hereby recommend acceptance of this dissertation. Tzi-cker Chiueh { Dissertation Advisor Professor, Department of Computer Science Jie Gao { Chairperson of Defense Associate Professor, Department of Computer Science Rob Johnson Assistant Professor, Department of Computer Science Ted Teng Professor, Department of Technology and Society This dissertation is accepted by the Graduate School. Charles Taber Interim Dean of the Graduate School ii Abstract of the Dissertation Optimization Techniques for Memory Virtualization-based Resource Management by Jui-Hao Chiang Doctor of Philosophy in Computer Science Stony Brook University 2012 Memory virtualization abstracts the physical memory resources in a virtualized server in such a way that offers many resource man- agement advantages, such as consolidation, sharing,
    [Show full text]
  • CMSC 331 Final Exam Section 0201 – December 18, 2000
    CMSC 331 Final Exam Section 0201 – December 18, 2000 Name: ___Answers_______________________ Student ID#:_____________________________ You will have two hours to complete this closed book exam. We reserve the right to assign partial credit, and to deduct points for answers that are needlessly wordy. 0. Logic (0) The multiple-choice question below has only one correct answer. Which one is correct? (a) Answer (a) or (b) 0 00/ (b) Answer (b) or (c) 1 20/ (c) Answer (c) 2 10/ 1. General multiple-choice questions (20) 3 15/ 4 40/ 1. Which kind of variable has the longest lifetime? 5 10/ (a) An implicitly heap-dynamic variable 6 10/ (b) A static variable (c) A stack-dynamic variable 7 20/ (d) A flexible variable 8 20/ (e) A fixed-length variable 9 10/ (f) A lexically scoped variable 10 15/ 11 15/ 2. Which of the following is true of aliases? (a) An alias changes the name of something 12 10/ (b) An alias protects an existing value from being overwritten 13 10/ (c) An alias provides an alternative way of accessing something 14 15/ (d) An alias allows type inference 15 20/ (e) Aliases should be avoided if at all possible (f) Aliases support name equivalence of record types * 240/ 3. What happens in an assignment such as ``x := y''? (a) The address of x is modified to be the address of y (b) The address of y is modified to be the address of x (c) The object bound to y is copied and bound to x, and any previous binding of x to an object is lost (d) x and y become aliases 4.
    [Show full text]
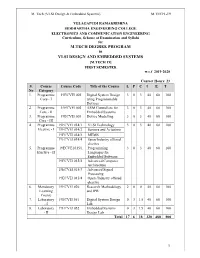
  • M.Tech Degree Program Vlsi Design and Embedded Systems
    M. Tech (VLSI Design & Embedded Systems) M.TECH -19 VELAGAPUDI RAMAKRISHNA SIDDHARTHA ENGINEERING COLLEGE ELECTRONICS AND COMMUNICATION ENGINEERING Curriculum, Scheme of Examination and Syllabi for M.TECH DEGREE PROGRAM in VLSI DESIGN AND EMBEDDED SYSTEMS [M.TECH 19] FIRST SEMESTER w.e.f 2019-2020 Contact Hours: 23 S. Course Course Code Title of the Course L P C I E T No Category 1. Programme 19ECVE1001 Digital System Design 3 0 3 40 60 100 Core - I using Programmable Devices 2. Programme 19ECVE1002 ARM Controllers for 3 0 3 40 60 100 Core - II Embedded Systems 3. Programme 19ECVE1003 Device Modelling 3 0 3 40 60 100 Core - III 4. Programme 19ECVE1014/1 VLSI Technology 3 0 3 40 60 100 Elective - I 19ECVE1014/2 Sensors and Actuators 19ECVE1014/3 MEMS 19ECVE1014/4 Open/Industry offered elective 5. Programme 19ECVE1015/1 Programming 3 0 3 40 60 100 Elective - II Languages for Embedded Software 19ECVE1015/2 Advanced Computer Architecture 19ECVE1015/3 Advanced Signal Processing 19ECVE1015/4 Open /Industry offered elective 6. Mandatory 19ECVE1026 Research Methodology 2 0 0 40 60 100 Learning and IPR Course 7. Laboratory 19ECVE1051 Digital System Design 0 3 1.5 40 60 100 - I Lab 8. Laboratory 19ECVE1052 Embedded Systems 0 3 1.5 40 60 100 - II Design Lab Total 17 6 18 320 480 800 1 M. Tech (VLSI Design & Embedded Systems) M.TECH -19 VELAGAPUDI RAMAKRISHNA SIDDHARTHA ENGINEERING COLLEGE ELECTRONICS AND COMMUNICATION ENGINEERING Curriculum, Scheme of Examination and Syllabi for M.TECH DEGREE PROGRAM in VLSI DESIGN AND EMBEDDED SYSTEMS [M.TECH 19] SECOND SEMESTER Contact Hours: 25 S.
    [Show full text]