Some METAFONT Techniques Yannis Haralambous
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Resources Ton 'QX Repository (For Details, Contact Peter Ab- Bott, E-Mail Address Above)
TUGboat, Volume 10 (1989), No. 2 Janet users may obtain back issues from the As- Resources ton 'QX repository (for details, contact Peter Ab- bott, e-mail address above). DECnetISPAN users may obtain back issues from the European (con- Announcing (belatedly) -MAG tact Massimo Calvani, fisicaQastrpd.infn. it) or American (contact Ed Bell, 7388 : :bell) DECnet Don Hosek T)?J repositories. University of Illinois at Chicago Others with network access should send a mes- After being chided for not publicizing my electronic sage to archive-serverQsun.soe.clarkson.edu "magazine" enough, I have decided to make a formal with the first line being path followed by an address announcement of its availability to the 'J&X cornmu- from Clarkson to you, and then a line nity at large. get texmag texmag.v.nn What is =MAG? for each back issue desired where v is the volume number and nn the issue number. The line index WMAG is available free of charge to anyone reach- texmag will give a list of back issues available. able by electronic mail and is published approxi- A typical mail request may resemble: mately every two months. The subject material index t exmag generally falls somewhere between the somewhat get texmag texmag.l.08 chaotic (but still useful) correspondence of 'QXHAX and UKW, and the printed matter in TUGboat How do I submit articles to TEXMAG? and QXline. Some previous articles have included I was hoping you would ask. Articles are accepted an early version of Dominik Wujastyk's article on on all aspects of T)?J, M'QX, and METAFONT from fonts from TUB 9#2; an overview of the differ- specific information on interfacing graphics packages ent font files used by 'QX, METAFONT, and device with particular DVI drivers to general information drivers; macros for commutative diagrams and sim- on macro writing to product reviews to whatever ple chemical equations and many other topics. -

Font HOWTO Font HOWTO
Font HOWTO Font HOWTO Table of Contents Font HOWTO......................................................................................................................................................1 Donovan Rebbechi, elflord@panix.com..................................................................................................1 1.Introduction...........................................................................................................................................1 2.Fonts 101 −− A Quick Introduction to Fonts........................................................................................1 3.Fonts 102 −− Typography.....................................................................................................................1 4.Making Fonts Available To X..............................................................................................................1 5.Making Fonts Available To Ghostscript...............................................................................................1 6.True Type to Type1 Conversion...........................................................................................................2 7.WYSIWYG Publishing and Fonts........................................................................................................2 8.TeX / LaTeX.........................................................................................................................................2 9.Getting Fonts For Linux.......................................................................................................................2 -

Surviving the TEX Font Encoding Mess Understanding The
Surviving the TEX font encoding mess Understanding the world of TEX fonts and mastering the basics of fontinst Ulrik Vieth Taco Hoekwater · EuroT X ’99 Heidelberg E · FAMOUS QUOTE: English is useful because it is a mess. Since English is a mess, it maps well onto the problem space, which is also a mess, which we call reality. Similary, Perl was designed to be a mess, though in the nicests of all possible ways. | LARRY WALL COROLLARY: TEX fonts are mess, as they are a product of reality. Similary, fontinst is a mess, not necessarily by design, but because it has to cope with the mess we call reality. Contents I Overview of TEX font technology II Installation TEX fonts with fontinst III Overview of math fonts EuroT X ’99 Heidelberg 24. September 1999 3 E · · I Overview of TEX font technology What is a font? What is a virtual font? • Font file formats and conversion utilities • Font attributes and classifications • Font selection schemes • Font naming schemes • Font encodings • What’s in a standard font? What’s in an expert font? • Font installation considerations • Why the need for reencoding? • Which raw font encoding to use? • What’s needed to set up fonts for use with T X? • E EuroT X ’99 Heidelberg 24. September 1999 4 E · · What is a font? in technical terms: • – fonts have many different representations depending on the point of view – TEX typesetter: fonts metrics (TFM) and nothing else – DVI driver: virtual fonts (VF), bitmaps fonts(PK), outline fonts (PFA/PFB or TTF) – PostScript: Type 1 (outlines), Type 3 (anything), Type 42 fonts (embedded TTF) in general terms: • – fonts are collections of glyphs (characters, symbols) of a particular design – fonts are organized into families, series and individual shapes – glyphs may be accessed either by character code or by symbolic names – encoding of glyphs may be fixed or controllable by encoding vectors font information consists of: • – metric information (glyph metrics and global parameters) – some representation of glyph shapes (bitmaps or outlines) EuroT X ’99 Heidelberg 24. -
Using Fonts Installed in Local Texlive - Tex - Latex Stack Exchange
27-04-2015 Using fonts installed in local texlive - TeX - LaTeX Stack Exchange sign up log in tour help TeX LaTeX Stack Exchange is a question and answer site for users of TeX, LaTeX, ConTeXt, and related Take the 2minute tour × typesetting systems. It's 100% free, no registration required. Using fonts installed in local texlive I have installed texlive at ~/texlive . I have installed collectionfontsrecommended using tlmgr . Now, ~/texlive/2014/texmfdist/fonts/ has several folders: afm , cmap , enc , ... , vf . Here is the output of tlmgr info helvetic package: helvetic category: Package shortdesc: URW "Base 35" font pack for LaTeX. longdesc: A set of fonts for use as "dropin" replacements for Adobe's basic set, comprising: Century Schoolbook (substituting for Adobe's New Century Schoolbook); Dingbats (substituting for Adobe's Zapf Dingbats); Nimbus Mono L (substituting for Abobe's Courier); Nimbus Roman No9 L (substituting for Adobe's Times); Nimbus Sans L (substituting for Adobe's Helvetica); Standard Symbols L (substituting for Adobe's Symbol); URW Bookman; URW Chancery L Medium Italic (substituting for Adobe's Zapf Chancery); URW Gothic L Book (substituting for Adobe's Avant Garde); and URW Palladio L (substituting for Adobe's Palatino). installed: Yes revision: 31835 sizes: run: 2377k relocatable: No catdate: 20120606 22:57:48 +0200 catlicense: gpl collection: collectionfontsrecommended But when I try to compile: \documentclass{article} \usepackage{helvetic} \begin{document} Hello World! \end{document} It gives an error: ! LaTeX Error: File `helvetic.sty' not found. Type X to quit or <RETURN> to proceed, or enter new name. -

Proposal to Represent the Slashed Zero Variant of Empty
L2/15-268 Title: Proposal to Represent the Slashed Zero Variant of Empty Set Source: Barbara Beeton (American Mathematical Society), Asmus Freytag (ASMUS, Inc.), Laurențiu Iancu and Murray Sargent III (Microsoft Corporation) Status: Individual contribution Action: For consideration by the Unicode Technical Committee Date: 2015-10-30 Abstract As of Unicode Version 8.0, the symbol for empty set is encoded as the character U+2205 EMPTY SET, with no standardized variation sequences. In scientific publications, the symbol is typeset in one of three var- iant forms, chosen by notational style: a slashed circle, ∅, a slashed wide oval in the shape a letter, ∅, or a slashed narrow oval in the shape of a digit zero, . The slashed circle and the slashed zero forms are the most widely used, and correspond to the LaTeX commands \varnothing and \emptyset, respectively. Having one Unicode representation to map to, fonts that provide glyphs for more than one form of the symbol typically implement a stylistic variant or a mapping to a PUA code point. However, the wide- spread use of the slashed zero variant and its mapping to the main LaTeX command for the symbol, \emptyset, make it a candidate for a dedicated means to distinctly represent it in Unicode. This document evaluates three approaches for representing in Unicode the slashed zero variant of the empty set symbol and proposes a solution based on a variation sequence. Additional related characters resulting from the investigation and needed to complete the solution are also proposed for encoding. 1. The empty set symbol 1.1. Historical references The introduction of the modern symbol for the empty set is attributed to André Weil of the Nicholas Bourbaki group. -

Metatype Project: Creating Truetype Fonts Based on M
Metatype project: creating TrueType fonts based on Metafont Serge Vakulenko Cronyx Engineering, Moscow Russia [email protected] http://www.vak.ru/proj/metatype Abstract The purpose of Metatype project is the development of freeware TrueType fonts for generic user community. Metafont language is chosen for creating character glyphs. Currently, glyph im- ages are converted to cubic outlines using bitmap tracing algorithm, and then to conic outlines. Two font families are currently been under development as a part of Metatype project: 1. TeX font family, based on Computer Modern fonts by Donald E. Knuth, retaining their “look and feel”. A rich set of typefaces is available, including Roman, Sans Serif, Monotype and Math faces with Normal, Bold, Italic, Bold Italic, Narrow and Wide variations. 2. Maestro font family is designed, as a Times-lookalike. It also uses Computer Mod- ern sources, with a lot of modifications. Why TrueType? representation of text strings. Far-seeing operational sys- tems, such as Windows NT, provide support Unicode at The world becomes closer. Now we observe, how the a kernel level. Word-processors use Unicode for stor- Internet and globalization of economics cause increase age of documents (XML, RTF and other formats). The of intensity of contacts between representatives of dif- amount of Internet sites with Unicode encoding grows ferent peoples, cultures, races. The world becomes more every day. Cellular telephones use Unicode for Inter- and more multilingual. The computer branch for a long net browsing (WAP). The world is slowly moving toward time has realized this fact: the draft variant of standard Unicode. And TrueType seems to be a natural result of Unicode is dated 1989 [1]. -

THE MATHALPHA, AKA MATHALFA PACKAGE the Math Alphabets
THE MATHALPHA, AKA MATHALFA PACKAGE MICHAEL SHARPE The math alphabets normally addressed via the macros \mathcal, \mathbb, \mathfrak and \mathscr are in a number of cases not well-adapted to the LATEX math font structure. Some suffer from one or more of the following defects: • font sizes are locked into a sequence that was appropriate for metafont{generated rather than scalable fonts; • there is no option in the loading package to enable scaling; • the font metrics are designed for text rather than math mode, leading to awkward spacing, subscript placement and accent placement when used for the latter; • the means of selecting a set of math alphabets varies from package to package. The goal of this package is to provide remedies for the above, where possible. This means, in effect, providing virtual fonts with my personal effort at correcting the metric issues, rewriting the font-loading macros usually found in a .sty and/or .fd files to admit a scale factor in all cases, and providing a .sty file which is extensible and from which any such math alphabet may be specified using a standard recipe. For example, the following fonts are potentially suitable as targets for \mathcal or \mathscr and are either included as part of TEXLive 2011, as free downloads from CTAN or other free sources, or from commercial sites. cm % Computer Modern Math Italic (cmsy) euler % euscript rsfs % Ralph Smith Formal Script---heavily sloped rsfso % based on rsfs, much less sloped lucida % From Lucida New Math (commercial) mathpi % Adobe Mathematical Pi or clones thereof -

Optimal Use of Fonts on Linux
Optimal Use of Fonts on Linux Avi Alkalay Donovan Rebbechi Hal Burgiss Copyright © 2006 Avi Alkalay, Donovan Rebbechi, Hal Burgiss 2007−04−15 Revision History Revision 2007−04−15 15 Apr 2007 Revised by: avi Included support to SUSE installation for the RPM scriptlets on template spec file, listed SUSE as a BCI−enabled distro. Revision 2007−02−08 08 Feb 2007 Revised by: avi Fixed some typos, updated Luc's page URL, added DejaVu sections, added link to FC6 Freetype RPMs, added link to Debian MS Core fonts, and added reference to the gnome−font−properties command. Revision 2006−07−02 02 Jul 2006 Revised by: avi Included link to Debian FreeType BCI package, improved the glossary with Latin1 descriptions, more clear links on the webcore fonts section, instructions on how to rebuild source RPM packages in the BCI appendix, updated the freetype recompilation appendix to cover new versions of the lib, authorship section reorganized. Revision 2006−04−02 02 Apr 2006 Revised by: avi Included link to FC5 Freetype.bci contribution by Cody DeHaan. Revision 2006−03−25 25 Mar 2006 Revised by: avi Updated link to BCI Freetype RPMs to be more distro version specific. Revision 2005−07−19 19 May 2005 Revised by: avi Renamed Microsoft Fonts to Webcore Fonts, and links updated.Added X.org Subsystems section. Revision 2005−05−25 25 May 2005 Revised by: avi Comment related to web pages in the Microsoft Fonts section Revision 2005−05−10 10 May 2005 Revised by: avi Old section−based glossary converted to real DocBook glossary.Modernized terms and explanations on the glossary.Included concepts as charsets, Unicode and UTF−8 in the glossary. -
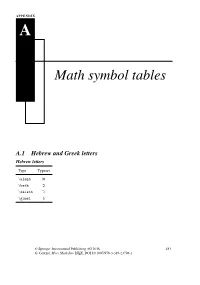
Math Symbol Tables
APPENDIX A Math symbol tables A.1 Hebrew and Greek letters Hebrew letters Type Typeset \aleph ℵ \beth ℶ \daleth ℸ \gimel ℷ © Springer International Publishing AG 2016 481 G. Grätzer, More Math Into LATEX, DOI 10.1007/978-3-319-23796-1 482 Appendix A Math symbol tables Greek letters Lowercase Type Typeset Type Typeset Type Typeset \alpha \iota \sigma \beta \kappa \tau \gamma \lambda \upsilon \delta \mu \phi \epsilon \nu \chi \zeta \xi \psi \eta \pi \omega \theta \rho \varepsilon \varpi \varsigma \vartheta \varrho \varphi \digamma ϝ \varkappa Uppercase Type Typeset Type Typeset Type Typeset \Gamma Γ \Xi Ξ \Phi Φ \Delta Δ \Pi Π \Psi Ψ \Theta Θ \Sigma Σ \Omega Ω \Lambda Λ \Upsilon Υ \varGamma \varXi \varPhi \varDelta \varPi \varPsi \varTheta \varSigma \varOmega \varLambda \varUpsilon A.2 Binary relations 483 A.2 Binary relations Type Typeset Type Typeset < < > > = = : ∶ \in ∈ \ni or \owns ∋ \leq or \le ≤ \geq or \ge ≥ \ll ≪ \gg ≫ \prec ≺ \succ ≻ \preceq ⪯ \succeq ⪰ \sim ∼ \approx ≈ \simeq ≃ \cong ≅ \equiv ≡ \doteq ≐ \subset ⊂ \supset ⊃ \subseteq ⊆ \supseteq ⊇ \sqsubseteq ⊑ \sqsupseteq ⊒ \smile ⌣ \frown ⌢ \perp ⟂ \models ⊧ \mid ∣ \parallel ∥ \vdash ⊢ \dashv ⊣ \propto ∝ \asymp ≍ \bowtie ⋈ \sqsubset ⊏ \sqsupset ⊐ \Join ⨝ Note the \colon command used in ∶ → 2, typed as f \colon x \to x^2 484 Appendix A Math symbol tables More binary relations Type Typeset Type Typeset \leqq ≦ \geqq ≧ \leqslant ⩽ \geqslant ⩾ \eqslantless ⪕ \eqslantgtr ⪖ \lesssim ≲ \gtrsim ≳ \lessapprox ⪅ \gtrapprox ⪆ \approxeq ≊ \lessdot -

A Module for Using METAFONT Directly Inside the Freetype Rasterizer 138 Tugboat, Volume 39 (2018), No
136 TUGboat, Volume 39 (2018), No. 2 FreeType MF Module: Fonts are the graphical representation of text A module for using METAFONT directly in a specific style and size. These fonts are mainly inside the FreeType rasterizer categorized in two types: outline fonts and bitmap fonts. Outline fonts are the most popular fonts for Jaeyoung Choi, Ammar Ul Hassan, producing high-quality output used in digital envi- Geunho Jeong ronments. However, to create a new font style as Abstract an outline font, font designers have to design a new font with consequent extensive cost and time. This METAFONT is a font description language which gen- recreation of font files for each variant of a font can erates bitmap fonts for the use by the T X system, E be especially painful for font designers in the case of printer drivers, and related programs. One advan- CJK fonts, which require designing of thousands in- tage of METAFONT over outline fonts is its capability dividual glyphs one by one. Compared to alphabetic for producing different font styles by changing pa- scripts, CJK scripts have both many more characters rameter values defined in its font specification file. and generally more complex shapes, expressed by Another major advantage of using METAFONT is combinations of radicals [3]. Thus it often takes more that it can produce various font styles like bold, than a year to design a CJK font set. italic, and bold-italic from one source file, unlike A programmable font language, METAFONT, outline fonts, which require development of a sepa- has been developed which does not have the above rate font file for each style in one font family. -

Creating Truetype Fonts Based on METAFONT
The METATYPE Project: Creating TrueType Fonts Based on METAFONT Serge Vakulenko Cronyx Engineering, Moscow, Russia [email protected] http://www.vak.ru/proj/metatype Abstract The purpose of the METATYPE project is the development of freeware TrueType fonts for the general user community. The METAFONT language was chosen for creating character glyphs. Currently, glyph images are converted to cubic outlines using a bitmap tracing algorithm, and then to conic outlines. Two font families are currently under development as part of the METATYPE project: the TeX font family, based on Computer Modern fonts by Donald E. Knuth, retaining their look and feel. A rich set of typefaces is available, including Roman, Sans Serif, Monowidth and Math faces with Normal, Bold, Italic, Bold Italic, Narrow and Wide variations; and second, the Maestro font family, which is designed as a Times look-alike. It also uses Computer Modern sources, but with numerous modifications. Résumé Le but du projet METATYPE est le développement de fontes TrueType libres pour la commu- nauté générale d’utilisateurs. Le langage de programmation METAFONT est utilisé pour créer les glyphes. Actuellement, les glyphes sont convertis d’abord en contours cubiques, en utilisant un al- gorithme d’auto-traçage de bitmap, et ensuite en contours coniques. Deux familles de fontes sont actuellement en développement, dans le cadre du projet META- TYPE : la famille «TeX font», basée sur les fontes Computer Modern de Donald E. Knuth, et proposant du romain, du sans empattements, du mono-chasse, et les fontes mathématiques, dans les styles : régulier, gras, italique, gras italique, étroitisé et élargi ; la famille «Maestro», qui est un clone du Times. -

Organization MFG Discussion Document Task 1
MFG discussion document Task 1: Organization 1 Summary of math font-related activities mote the use of MathML on the World Wide Web at EuroTEX '98 without being restricted to the symbol complement provided by the system fonts. 1 Introduction Information about the list of symbols collected The subject of math symbol fonts has been one of by the STIX project currently resides on internal the major topics of interest at the 10th European pages on the AMS Web server [2] and is kept in a TEX Conference (EuroTEX '98), which was held on format similar to the Unicode symbol tables [3], but March 29{31, 1998 at St. Malo, France as part of there are plans to release a printable version of these the 2nd Week on Electronic Publishing and Digital tables in PDF format to the general public soon. Typography (WEPT '98). It was pointed out that a printable version of During the conference a paper summarizing the the symbol tables from the MathML specification is 1 MFG supposed to be available in PDF format on the W3C activities of the Math Font Group ( ) [1] was 2 presented and two BOF sessions on math fonts were Web server [4]. The latest version of the MathML held, bringing together members of the MFG and specification also includes some background infor- representatives of other interested parties, such as mation about the STIX project and references to the W3C MathML working group, the STIX project, various other glyph collections [5, Chapter 6]. as well as publishers and typesetters. 3 Implementation of new 8-bit math fonts In addition, there were also many private dis- for (LA)TEX cussions on math fonts at lunches, dinners, and at informal get-togethers in the local caf´es or pubs.