DOCSLIB.ORG

Spin Liquid and Quantum Phase Transition Without Symmetry Breaking in a Frustrated Three-Dimensional Ising Model

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Spin Liquid and Quantum Phase Transition Without Symmetry Breaking in a Frustrated Three-Dimensional Ising Model Spin liquid and quantum phase transition without symmetry breaking in a frustrated three-dimensional Ising model Masterarbeit zur Erlangung des akademischen Grades Master of Science vorgelegt von Julia Röchner geboren in Herne Lehrstuhl für Theoretische Physik I Fakultät Physik Technische Universität Dortmund 2016 1. Gutachter : Prof. Dr. Kai P. Schmidt 2. Gutachter : Prof. Dr. Leon Balents Datum des Einreichens der Arbeit: 30. September 2016 Abstract In this thesis the transverse field Ising model on the three-dimensional pyrochlore lattice is investigated. This model is highly frustrated in the low-field limit which entails an extensively large ground-state degeneracy. Quantum fluctuations in the ground-state manifold at T = 0 are present and give rise to a Coulomb quantum spin liquid phase. Based on this knowledge the quantum phase transition without symmetry breaking between the polarized phase and the Coulomb quantum spin liquid phase is located quantitively. This is done by investigating the high- and low-field limit via perturbative continuous unitary transformation which allows to determine quantities exactly as series up to a certain order in a perturbation parameter. We show by extrapolating the bare series of the elementary excitation gap of the high-field limit that the model does not exhibit a second-order phase transition. Strong evidence for a first-order phase transition is gained by comparing and locating the crossing of the ground- state energies of both limits. Kurzfassung In dieser Arbeit wird das Ising-Modell im transversalen Magnetfeld auf dem dreidimensio- nalen Pyrochlorgitter untersucht. Dieses Modell ist im Limes kleiner Felder hoch frustriert, was eine extensiv große Grundzustandsentartung zur Folge hat. Quantenfluktuationen in der Grundzustandsmannigfaltigkeit bei T = 0 sind der Grund für die Existenz einer Coulomb Quanten-Spinflüssigkeitsphase. Basierend darauf wird der Quanten-Phasenübergang ohne Symmetriebrechung zwischen der polarisierten Phase und der Coulomb Quanten-Spinflüssig- keitsphase quantitativ bestimmt, indem der Hoch- und Niedrigfeldlimes mittels perturbativer kontinuierlicher unitärer Transformation untersucht wird, was eine exakte Reihenentwicklung von Größen bis zu einer bestimmten Ordnung im Perturbationsparameter ermöglicht. Durch Extrapolieren der nackten Reihe der elementaren Anregungslücke im Hochfeldlimes wird gezeigt, dass das Modell keinen Phasenübergang zweiter Ordnung aufweist. Stattdessen wird ein Phasenübergang erster Ordnung gefunden, der durch den Kreuzungspunkt der Grundzu- standsenergien im Hoch- und Niedrigfeldfall lokalisiert wird. IV Contents Table of Contents V 1 Introduction 1 2 Quantum spin ice 5 2.1 Water ice . .5 2.2 Spin ice . .6 2.3 Quantum effects . 10 3 Transverse Field Ising Model on the pyrochlore lattice 13 3.1 Model . 13 3.2 Particle representation . 18 3.2.1 High-field limit . 18 3.2.2 Low-field limit . 20 4 Series expansion methods 24 4.1 Perturbative Continuous Unitary Transformation . 24 4.1.1 Continuous Unitary Transformation . 24 4.1.2 Perturbative CUT . 27 4.1.3 Cluster decomposition and cluster additivity . 29 4.2 Extrapolation . 30 4.2.1 Pad´e-approximation . 30 4.2.2 DlogPad´e-extrapolation . 31 V 5 Full graph decomposition 32 5.1 Graph representation . 32 5.2 Graph generation . 33 5.3 Reduced energies . 36 5.4 Graph embedding in lattice . 38 5.4.1 Ground state . 38 5.4.2 Hopping elements . 40 5.5 Loop graphs . 41 6 Results 42 6.1 High-field limit . 43 6.2 Low-field limit . 51 6.3 Comparison of both limits . 53 6.4 Experimental realization . 54 7 Conclusion and outlook 56 A One-particle gap of antiferromagnetic TFIM on kagome lattice 60 B One-particle gap of ferromagnetic TFIM on kagome lattice 61 Bibliography 67 VI Chapter 1 Introduction In condensed matter physics the study of phase transitions in strongly correlated systems displays an exciting field in theory as well as in experiment. Different phases in materials are distinguishable by their macroscopic properties. The likely most popular example of a phase transition is the one when water freezes to ice. In the fluid phase the H20 molecules ◦ are disordered, while for temperatures below the critical value Tc = 0 C, the system orders and the molecules form a crystalline structure. The terms "order" and "disorder" can also be defined in the realm of magnetism on a spin level, where "spin" corresponds to the orientation of magnetic moments caused by atoms in a compound. If we consider ferromagneticly coupled spins residing on the sites of a square lattice, the system is in the disordered paramagnetic phase for high temperatures. Below a critical value Tc, the system orders and takes one of the ground states, where all spins follow a parallel ordering according to the ferromagnetic coupling (see Fig. 1.1). The ordered state spontaneously breaks the symmetry, since it has lower symmetry than the Hamiltonian. Note that the phase transitions described above are classical because they are induced by temperature change. In contrast to that, there can also occur phase transitions at T = 0, if materials show strong quantum effects. Those transitions are then called quantum phase transitions, which are for example generated by intrinsic or applied electric or mag- netic fields. While phase transitions engendered by symmetry breaking are well known and extensively studied, phases without broken symmetries receive high attention, since they are prone to host fascinating and exotic properties. The most common examples are phase tran- sitions generated by topological order [1–5]. Phase transitions without symmetry breaking in some other materials can be traced back to occurring frustration [6]. Frustration happens, if competing interactions in materials cannot be simultaneously satisfied usually due to the 1 2 Chapter 1. Introduction Figure 1.1: Sketch of phase diagram of ferromagneticly coupled spins on square lattice. For low temperatures T < Tc the system is ordered while for high temperatures T > Tc the system is disordered and in a paramagnetic phase. geometric arrangement of the magnetic moments. This entails, that not only one or a few classical spin configurations in the material minimize the energy, but instead the number of ground states is extensively large inducing highly entangled states in case quantum effects play a significant role. Generically, frustration gives rise to exotic phenomena in materials and can lead, under certain conditions, to a classical or quantum spin liquid state, similar to the disorder of molecules in real liquids. Spin liquids are disordered states with fractional excitations which do not break any symmetries [7]. Due to the large ground-state degeneracy of classical spin liquids, fluctuations, mainly in the ground-state manifold, occur down to very low temperatures, which can be either classical or quantum. Especially if the origin lies in quantum effects, one expects to observe exotic properties. The study of frustrated magnets therefore aroused great interest in the past. There has been much work on two-dimensional frustrated systems, for example antiferromagneticly coupled spins on the triangular or kagome lattice [8,10]. In turn, three-dimensional frustrated systems are much more complicated, since their dimensionality makes a microscopic investigation difficult, which is simultaneously the same reason why it has become an exciting and very challenging field of research. The most storied three-dimensional examples are the spin ice pyrochlores Ho2Ti2O7 or Dy2Ti2O7, where strong geometric frustration among coupled magnetic moments gives rise to classical spin liquids with defects that behave like magnetic monopoles [11,12]. However, quantum effects are essentially zero in these spin-ice compounds, 3 z which are described accurately by classical Ising models, i. e. only the (local) σi component of the spins appears in the Hamiltonian. However, theoretically, a quantum version of spin ice is highly desirable. One expects the presence of a so-called Coulomb quantum spin liquid (CQSL) [7, 13, 14] with gapped electric and magnetic excitations as well as an emergent gapless photon. Quantum fluctuations may be introduced by additional exchange interactions involving spin flips (e. g. XY or more complex couplings), which naturally occur in some other pyrochlores like Yb2Ti2O7 [15,16]. However, such quantum exchange models are quite complex, and their phase diagrams contain many other ground states in addition to the desired CQSL [18, 19]. At the model Hamiltonian level, a simpler route to "quantum-ize" classical spin ice is to add a transverse field. The low-energy physics of such systems is expected to be described to a good extent by the transverse-field Ising model (TFIM) on the three-dimensional pyrochlore lattice, which is depicted in Fig. 1.2. Figure 1.2: Illustration of the pyrochlore lattice, which consists out of alternating up- and down– pointing corner-sharing tetrahedra. The TFIM is one of the archetypal models used in various areas in physics and is known to host a plethora of interesting physical phenomena, especially on highly frustrated lattices [8–10,20]. At the same time the theoretical treatment of three-dimensional frustrated systems including TFIMs represents a notable challenge and quantitative results are hard to extract since common standard methods, for example exact diagonalization, are inefficient due to the rapidly growing cluster. In turn, series expansions operating in the thermodynamic limit scale well with the dimension and are well suited to treat TFIMs on three-dimensional
Load more

Recommended publications
  • Phase Transitions in Quantum Condensed Matter
    Diss. ETH No. 15104 Phase Transitions in Quantum Condensed Matter A dissertation submitted to the SWISS FEDERAL INSTITUTE OF TECHNOLOGY ZURICH¨ (ETH Zuric¨ h) for the degree of Doctor of Natural Science presented by HANS PETER BUCHLER¨ Dipl. Phys. ETH born December 5, 1973 Swiss citizien accepted on the recommendation of Prof. Dr. J. W. Blatter, examiner Prof. Dr. W. Zwerger, co-examiner PD. Dr. V. B. Geshkenbein, co-examiner 2003 Abstract In this thesis, phase transitions in superconducting metals and ultra-cold atomic gases (Bose-Einstein condensates) are studied. Both systems are examples of quantum condensed matter, where quantum effects operate on a macroscopic level. Their main characteristics are the condensation of a macroscopic number of particles into the same quantum state and their ability to sustain a particle current at a constant velocity without any driving force. Pushing these materials to extreme conditions, such as reducing their dimensionality or enhancing the interactions between the particles, thermal and quantum fluctuations start to play a crucial role and entail a rich phase diagram. It is the subject of this thesis to study some of the most intriguing phase transitions in these systems. Reducing the dimensionality of a superconductor one finds that fluctuations and disorder strongly influence the superconducting transition temperature and eventually drive a superconductor to insulator quantum phase transition. In one-dimensional wires, the fluctuations of Cooper pairs appearing below the mean-field critical temperature Tc0 define a finite resistance via the nucleation of thermally activated phase slips, removing the finite temperature phase tran- sition. Superconductivity possibly survives only at zero temperature.
    [Show full text]
  • The Superconductor-Metal Quantum Phase Transition in Ultra-Narrow Wires
    The superconductor-metal quantum phase transition in ultra-narrow wires Adissertationpresented by Adrian Giuseppe Del Maestro to The Department of Physics in partial fulfillment of the requirements for the degree of Doctor of Philosophy in the subject of Physics Harvard University Cambridge, Massachusetts May 2008 c 2008 - Adrian Giuseppe Del Maestro ! All rights reserved. Thesis advisor Author Subir Sachdev Adrian Giuseppe Del Maestro The superconductor-metal quantum phase transition in ultra- narrow wires Abstract We present a complete description of a zero temperature phasetransitionbetween superconducting and diffusive metallic states in very thin wires due to a Cooper pair breaking mechanism originating from a number of possible sources. These include impurities localized to the surface of the wire, a magnetic field orientated parallel to the wire or, disorder in an unconventional superconductor. The order parameter describing pairing is strongly overdamped by its coupling toaneffectivelyinfinite bath of unpaired electrons imagined to reside in the transverse conduction channels of the wire. The dissipative critical theory thus contains current reducing fluctuations in the guise of both quantum and thermally activated phase slips. A full cross-over phase diagram is computed via an expansion in the inverse number of complex com- ponents of the superconducting order parameter (equal to oneinthephysicalcase). The fluctuation corrections to the electrical and thermal conductivities are deter- mined, and we find that the zero frequency electrical transport has a non-monotonic temperature dependence when moving from the quantum critical to low tempera- ture metallic phase, which may be consistent with recent experimental results on ultra-narrow MoGe wires. Near criticality, the ratio of the thermal to electrical con- ductivity displays a linear temperature dependence and thustheWiedemann-Franz law is obeyed.
    [Show full text]
  • Spin Liquids
    Experimental Candidates of Quantum Spin Liquids CURRENT STATUS RRP Singh UC DAVIS Experimental Candidates of Quantum Spin Liquids Where do they stand RRP Singh UC DAVIS OUTLINE • What is a Quantum Spin Liquid? • Experimental candidates Why they were considered as QSL Are their alternative explanations for observed behavior? • Discussion: What would be convincing of a Quantum Spin Liquid? ---Challenge for experiments and numerical studies What is a Quantum Spin Liquid? • A simple-minded perspective • Liquid : Condensed Yet Fluid (Dynamical) Phase • Quantum Liquid: Coherent Quantum Dynamics • Not necessarily Macro Quantum Phenomena? • Translational Motion of Atoms: (He) Phase Diagram Assembly of Interacting Quantum Spins • Nearly ideal paramagnet is like a gas • Ordered FM/AFM is like a solid • In between one can have a spin-liquid Strong Short-range order, yet not frozen Not FM/AFM/Helical/Spiral/Spin-glass • Is there a Quantum Spin Liquid? Must exist down to low temperatures possibly T=0 Likely associated with small spin (1/2 OR 1) Spin Liquids Classical and QSL L. Balents Nature 464 199 (2010) Spin Ice are examples of classical spin- liquids where theory and experimental signatures are on much firmer footing. We focus on Quantum Spin Liquids Exclusions from QSL Pair of AFM coupled spins form fully entangled rotationally invariant singlet states --cluster of even number of spin-1/2 --which decouple from the rest Let us exclude systems that by material geometry decouple into (adiabatically connect to) finite systems ( decoupled spin clusters
    [Show full text]
  • Quantum Phase Transitions
    INSTITUTE OF PHYSICS PUBLISHING REPORTS ON PROGRESS IN PHYSICS Rep. Prog. Phys. 66 (2003) 2069–2110 PII: S0034-4885(03)33852-7 Quantum phase transitions Matthias Vojta Institut fur¨ Theorie der Kondensierten Materie, Universitat¨ Karlsruhe, Postfach 6980, D-76128 Karlsruhe, Germany E-mail: [email protected] Received 1 August 2003, in final form 8 October 2003 Published 3 November 2003 Online at stacks.iop.org/RoPP/66/2069 Abstract In recent years, quantum phase transitions have attracted the interest of both theorists and experimentalists in condensed matter physics. These transitions, which are accessed at zero temperature by variation of a non-thermal control parameter, can influence the behaviour of electronic systems over a wide range of the phase diagram. Quantum phase transitions occur as a result of competing ground state phases. The cuprate superconductors which can be tuned from a Mott insulating to a d-wave superconducting phase by carrier doping are a paradigmatic example. This review introduces important concepts of phase transitions and discusses the interplay of quantum and classical fluctuations near criticality. The main part of the article is devoted to bulk quantum phase transitions in condensed matter systems. Several classes of transitions will be briefly reviewed, pointing out, e.g., conceptual differences between ordering transitions in metallic and insulating systems. An interesting separate class of transitions is boundary phase transitions where only degrees of freedom of a subsystem become critical; this will be illustrated in a few examples. The article is aimed at bridging the gap between high- level theoretical presentations and research papers specialized in certain classes of materials.
    [Show full text]
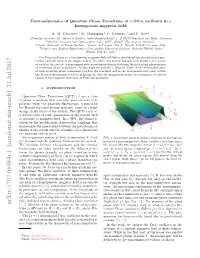
  • Thermodynamics of Quantum Phase Transitions of a Dirac Oscillator in a Homogenous Magnetic field
    Thermodynamics of Quantum Phase Transitions of a Dirac oscillator in a homogenous magnetic field A. M. Frassino,1 D. Marinelli,2 O. Panella,3 and P. Roy4 1Frankfurt Institute for Advanced Studies, Ruth-Moufang-Straße 1, D-60438 Frankfurt am Main, Germany 2Machine Learning and Optimization Lab., RIST, 400487 Cluj-Napoca, Romania∗ 3Istituto Nazionale di Fisica Nucleare, Sezione di Perugia, Via A. Pascoli, I-06123 Perugia, Italyy 4Physics and Applied Mathematics Unit, Indian Statistical Institute, Kolkata-700108, India (Dated: July 24, 2017) The Dirac oscillator in a homogenous magnetic field exhibits a chirality phase transition at a par- ticular (critical) value of the magnetic field. Recently, this system has also been shown to be exactly solvable in the context of noncommutative quantum mechanics featuring the interesting phenomenon of re-entrant phase transitions. In this work we provide a detailed study of the thermodynamics of such quantum phase transitions (both in the standard and in the noncommutative case) within the Maxwell-Boltzmann statistics pointing out that the magnetization has discontinuities at critical values of the magnetic field even at finite temperatures. I. INTRODUCTION Quantum Phase Transitions (QPT) [1] are a class of phase transitions that can take place at zero tem- perature when the quantum fluctuations, required by the Heisenberg's uncertainty principle, cause an abrupt change in the phase of the system. The QPTs occur at a critical value of some parameters of the system such as pressure or magnetic field. In a QPT, the change is driven by the modification of particular couplings that characterise the interactions between the microscopic el- ements of the system and the dynamics of its phase near the quantum critical point.
    [Show full text]
  • Heavy Fermions and Quantum Phase Transitions Qimiao Si and Frank Steglich
    REVIEW non-Fermi liquid behavior (9), which goes beyond the standard theory of metals [Fermi- liquid theory (10)], is another phenomenon that is Heavy Fermions and broadly relevant to the physics of strongly cor- related systems (11, 12). Quantum Phase Transitions Quantum criticality has been implicated to one degree or another in a host of other heavy- fermion metals (4, 13, 14). These include CeCu2Si2, 1 2 Qimiao Si * and Frank Steglich * the first superconductor to be observed among heavy-fermion metals (15), and CeRhIn5 (Fig. Quantum phase transitions arise in many-body systems because of competing interactions that promote 1C) (16). Extensive theoretical studies have led – rivaling ground states. Recent years have seen the identification of continuous quantum phase transitions, to unconventional quantum criticality (17 20). or quantum critical points, in a host of antiferromagnetic heavy-fermion compounds. Studies of the More recently, a plethora of phases have been interplay between the various effects have revealed new classes of quantum critical points and are uncovered in heavy-fermion metals near a QCP b uncovering a plethora of new quantum phases. At the same time, quantum criticality has provided [such as in Ir-doped YbRh2Si2 (8)andin -YbAlB4 fresh insights into the electronic, magnetic, and superconducting properties of the heavy-fermion metals. (21)]. Together with the theoretical studies of the We review these developments, discuss the open issues, and outline some directions for future research. global phase diagram of the heavy-fermion metals (22, 2), these developments open up an entirely new frontier on the interplay between quantum critical- uantum mechanics not only governs the uent particles.
    [Show full text]
  • Computing Quantum Phase Transitions Preamble
    COMPUTING QUANTUM PHASE TRANSITIONS Thomas Vojta Department of Physics, University of Missouri-Rolla, Rolla, MO 65409 PREAMBLE: MOTIVATION AND HISTORY A phase transition occurs when the thermodynamic properties of a material display a singularity as a function of the external parameters. Imagine, for instance, taking a piece of ice out of the freezer. Initially, its properties change only slowly with increasing temperature. However, at 0°C, a sudden and dramatic change occurs. The thermal motion of the water molecules becomes so strong that it destroys the crystal structure. The ice melts, and a new phase of water forms, the liquid phase. At the phase transition temperature of 0°C the solid (ice) and the liquid phases of water coexist. A finite amount of heat, the so-called latent heat, is required to transform the ice into liquid water. Phase transitions involving latent heat are called first-order transitions. Another well known example of a phase transition is the ferromagnetic transition of iron. At room temperature, iron is ferromagnetic, i.e., it displays a spontaneous magnetization. With rising temperature, the magnetization decreases continuously due to thermal fluctuations of the spins. At the transition temperature (the so-called Curie point) of 770°C, the magnetization vanishes, and iron is paramagnetic at higher temperatures. In contrast to the previous example, there is no phase coexistence at the transition temperature; the ferromagnetic and paramagnetic phases rather become indistinguishable. Consequently, there is no latent heat. This type of phase transition is called continuous (second-order) transition or critical point. Phase transitions play an essential role in shaping the world.
    [Show full text]
  • QUANTUM PHASE TRANSITIONS in DISORDERED MAGNETS by DAVID NOZADZE a DISSERTATION Presented to the Faculty of the Graduate School
    QUANTUM PHASE TRANSITIONS IN DISORDERED MAGNETS by DAVID NOZADZE A DISSERTATION Presented to the Faculty of the Graduate School of the MISSOURI UNIVERSITY OF SCIENCE AND TECHNOLOGY In Partial Fulfillment of the Requirements for the Degree DOCTOR OF PHILOSOPHY in PHYSICS 2013 Approved by Dr. Thomas Vojta, Advisor Dr. Paul Parris Dr. Julia E. Medvedeva Dr. Gerald Wilemski Dr. Ribhu Kaul Copyright 2013 DAVID NOZADZE All Rights Reserved iii DEDICATION I dedicate this dissertation to my mother Eteri Lebanidze. Her support and encouragement have sustained me throughout my life. Also, this dissertation is dedicated to the memory of my deceased father Vladimer Nozadze. Gone now but never forgotten. I will miss him always and love him forever. iv PUBLICATION DISSERTATION OPTION This dissertation has been prepared in the form of six papers. Paper I, pages 46–64 had been published as Composition-tuned smeared phase transitions, Physical Review B 83, 224402 (2011) with Fawaz Hrahsheh, and Thomas Vojta. Pa- per II, pages 65–80 had been published as Disorder correlations at smeared phase transitions, Europhysics Letters 97, 20007 (2012) with Christopher Svoboda, Fawaz Hrahsheh, and Thomas Vojta. Paper III, pages 81–90 had been published as Disorder promotes ferromagnetism: Rounding of the quantum phase transition in Sr1−xCaxRuO3, Physical Review Letters 108, 185701 (2012) with L. Demk´o, S. Bord´acs, T. Vojta, F. Hrahsheh, C. Svoboda, B. D´ora, H. Yamada, M. Kawasaki, Y. Tokura, and I. K´ezsm´arki. Paper IV, pages 91–110 had been published as Quantum Griffiths singu- larities in ferromagnetic metals, Physical Review B 85, 174202 (2012) with Thomas Vojta, selected as an Editor’s Suggestion.
    [Show full text]
  • Discovery of an Ultra-Quantum Spin Liquid
    Discovery of an ultra-quantum spin liquid Yanxing Yang Fudan University Cheng Tan Fudan University Zihao Zhu Fudan University J. Zhang Fudan University Zhaofeng Ding Fudan University Qiong Wu Fudan University Changsheng Chen Fudan University Toni Shiroka Paul Scherrer Institut Douglas MacLaughline University of California, Riverside Chandra Varma University of California-Berkeley Lei Shu ( [email protected] ) Fudan University Article Keywords: Quantum Fluctuations, Thermodynamic Properties, Muon Relaxation Rates, Invariant Time- dependent Fluctuations, Topological Singlet Excitations Posted Date: April 2nd, 2021 DOI: https://doi.org/10.21203/rs.3.rs-351743/v1 License: This work is licensed under a Creative Commons Attribution 4.0 International License. Read Full License Discovery of an ultra-quantum spin liquid Y. X. Yang1, C. Tan1, Z. H. Zhu1, J. Zhang1, Z. F. Ding1, Q. Wu1, C. S. Chen1, T. Shiroka2, D. E. MacLaughlin3, C. M. Varma4∗, & L. Shu1,5,6∗ 1State Key Laboratory of Surface Physics, Department of Physics, Fudan University, Shanghai 200433, China 2Laboratory for Muon-Spin Spectroscopy, Paul Scherrer Institut, 5232 Villigen, Switzerland 3Department of Physics and Astronomy, University of California, Riverside, CA 92521, USA 4Department of Physics, University of California, Berkeley, CA 94704, USA 5Collaborative Innovation Center of Advanced Microstructures, Nanjing 210093, China 6Shanghai Research Center for Quantum Sciences, Shanghai 201315, China ∗Corresponding authors. Email: [email protected] (C.M.V.); [email protected] (L.S.). Quantum fluctuations are expected to lead to highly entangled spin-liquid states in some two-dimensional spin-1/2 compounds. We have synthesized and measured thermodynamic properties and muon relaxation rates in two related such compounds, one of which is the least disordered of this kind synthesized hitherto and reveals intrinsic properties of a class of spin-liquids.
    [Show full text]
  • Kaleidoscope of Exotic Quantum Phases in a Frustrated XY Model
    Kaleidoscope of exotic quantum phases in a frustrated XY model Christopher N. Varney,1,2 Kai Sun,1,3 Victor Galitski,1,3 and Marcos Rigol2 1Joint Quantum Institute and Department of Physics, University of Maryland, College Park, Maryland 20742, USA 2Department of Physics, Georgetown University, Washington, DC 20057, USA and 3Condensed Matter Theory Center, Department of Physics, University of Maryland, College Park, Maryland 20742, USA The existence of quantum spin liquids was first conjectured by Pomeranchuk some seventy years ago, who argued that frustration in simple antiferromagnetic theories could result in a Fermi-liquid- like state for spinon excitations. Here we show that a simple quantum spin model on a honeycomb lattice hosts the long sought-for Bose metal with a clearly identifiable Bose-surface. The complete phase diagram of the model is determined via exact diagonalization and is shown to include four distinct phases separated by three quantum phase transitions. PACS numbers: 75.10.Kt, 67.85.Jk, 21.60.Fw, 75.10.Jm We learn early in our education that as matter is cooled (a) I II III IV down to low temperatures it normally experiences tran- Spin Anti-ferromagnet Spin Wave 120Ê Order sitions into ordered states of various kinds - crystalline Liquid solid structures, ordered magnetic phases, superfluid and 10-1 100 superconducting states, etc. It is also common knowledge J2 / J1 that upon heating the matter, the ordered phases melt (b) (c) (d) into the familiar gaseous or liquid classical states that we encounter routinely in our everyday lives. A more specialized but equally well-established result is that no order can survive in one-dimensional systems [1], because quantum zero-point motion acts there similarly to ther- mal effects and “quantum-melts” ordered phases even at zero temperature.
    [Show full text]
  • Quantum Spin Liquids Unveil the Genuine Mott State
    LETTERS https://doi.org/10.1038/s41563-018-0140-3 Quantum spin liquids unveil the genuine Mott state A. Pustogow 1*, M. Bories1, A. Löhle1, R. Rösslhuber1, E. Zhukova2, B. Gorshunov2, S. Tomić3, J. A. Schlueter4,5, R. Hübner 1,6, T. Hiramatsu7, Y. Yoshida7,8, G. Saito7,9, R. Kato10, T.-H. Lee11, V. Dobrosavljević11, S. Fratini 12 and M. Dressel1 The localization of charge carriers by electronic repulsion provides interesting analogies to supercritical liquids and gases6,7. was suggested by Mott in the 1930s to explain the insulating This physical picture emerges from the state-of-the-art dynamical state observed in supposedly metallic NiO. The Mott metal– mean-field theory (DMFT) description, which succeeds in captur- insulator transition has been subject of intense investigations ing most salient features of the Mott point. The generic perspective, ever since1–3—not least for its relation to high-temperature however, also reveals striking differences to conventional liquids, superconductivity4. A detailed comparison to real materials, which usually form a solid on cooling or compression. Indeed, in however, is lacking because the pristine Mott state is com- classical solidification, the well-ordered crystal phase typically pos- monly obscured by antiferromagnetism and a complicated sesses a reduced entropy because the continuous rotational and band structure. Here we study organic quantum spin liquids, translational symmetry that characterizes the liquid is spontane- prototype realizations of the single-band Hubbard model in ously broken. The opposite behaviour, however, is observed for the absence of magnetic order. Mapping the Hubbard bands interacting electrons subject to Mott–Hubbard correlations, which by optical spectroscopy provides an absolute measure of the is reminiscent of the paradigmatic Fermi liquid 3He below T =​ 0.3 K: interaction strength and bandwidth—the crucial parameters heating the fluid (under a pressure of about 3 MPa) transforms it that enter calculations.
    [Show full text]
  • Quantum Spin Liquid Candidate Becomes a Superconductor Under Pressure – Physics World
    2020/10/18 Quantum spin liquid candidate becomes a superconductor under pressure – Physics World SUPERCONDUCTIVITY RESEARCH UPDATE Quantum spin liquid candidate becomes a superconductor under pressure 15 Oct 2020 Isabelle Dumé Pressure-temperature (P-T) phase diagram of a NaYbSe2 single crystal. Courtesy: Run-Ze Yu Researchers in China report that they have observed both superconductivity and an insulator-to-metal transition in sodium ytterbium (III) selenide (NaYbSe2) simply by applying pressure to it. This inorganic substance, which is also a quantum spin liquid (QSL) candidate, could therefore become a new platform for investigating superconductivity in compounds that have electrons in their f orbitals, and for exploring the mechanisms of unconventional superconductivity in these materials. Quantum spin liquids (QSLs) are solid magnetic materials that cannot arrange their magnetic moments (or spins) into a regular and stable pattern. This behaviour contrasts with that of ordinary ferromagnets, in which all the spins point in the same direction, or antiferromagnets, in which the spins point in alternating directions. Instead, the spins in a QSL constantly change direction in a fluid-like way – even at ultracold temperatures near absolute zero – and are thus said to be “frustrated”. The late physicist and Nobel laureate Philip W Anderson proposed the existence of QSLs in the early 1970s, when he was studying the ground state of antiferromagnetically interacting spins on a triangular crystal lattice. Although Anderson did not follow up the idea at the time, he returned to it in 1986 after the discovery of high-temperature superconductivity in copper oxides (cuprates). A year later, his work bore fruit when he uncovered a potentially crucial link between QSL theory and “unconventional” high- temperature superconductivity.
    [Show full text]