EMC Effect and Color Fluctuations in Nucleons
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
Arxiv:1611.09748V4 [Nucl-Ex] 13 Apr 2017 1
Nucleon-Nucleon Correlations, Short-lived Excitations, and the Quarks Within Or Hen Massachusetts Institute of Technology, Cambridge, MA 02139 Gerald A. Miller Department of Physics, University of Washington, Seattle, WA 98195 Eli Piasetzky School of Physics and Astronomy, Tel Aviv University, Tel Aviv 69978, Israel Lawrence B. Weinstein Department of Physics, Old Dominion University, Norfolk, VA 23529 (Dated: April 17, 2017) This article reviews our current understanding of how the internal quark structure of a nucleon bound in nuclei differs from that of a free nucleon. We focus on the interpre- tation of measurements of the EMC effect for valence quarks, a reduction in the Deep Inelastic Scattering (DIS) cross-section ratios for nuclei relative to deuterium, and its possible connection to nucleon-nucleon Short-Range Correlations (SRC) in nuclei. Our review and new analysis (involving the amplitudes of non-nucleonic configurations in the nucleus) of the available experimental and theoretical evidence shows that there is a phenomenological relation between the EMC effect and the effects of SRC that is not an accident. The influence of strongly correlated neutron-proton pairs involving highly virtual nucleons is responsible for both effects. These correlated pairs are temporary high-density fluctuations in the nucleus in which the internal structure of the nucleons is briefly modified. This conclusion needs to be solidified by the future experiments and improved theoretical analyses that are discussed herein. Contents 1. Nucleons only 23 2. Nucleons plus pions 24 D. Beyond Conventional Nuclear Physics: Nucleon I. Introduction - Short Range Correlations (SRC) and Modification 25 Nuclear Dynamics 2 1. Mean field 26 A. -
Analysis of Neutron Stars Observations Using a Correlated Fermi Gas Model Short-Range Correlations in N/Z Asymmetric Nuclei O
6th International Symposium on Nuclear Symmetry Energy (NuSYM16) June 13- June 17, 2016, Tsinghua University, Beijing, China Analysis of Neutron Stars Observations Using a Correlated Fermi Gas Model short-range correlations in N/Z asymmetric nuclei O. Hen, A.W. Steiner, E. Piasetzky, neutronand L.B.-proton Weinstein momentum distributions Two Fermions systems and the Contact term SRC role in the nuclear equation of state Eli Piasetzky Tel Aviv University ISRAEL Short Range (tensor) Correlations in nuclei Hard Semi inclusive scattering A(e, e’p) Only 60-70% of the expected single-particle strength. SRC and LRC 2N-SRC ~1 fm ≤1.f K 1 1.7f 1.7 fm Krel > K F K < K ρ = 0.16 GeV/fm3 Nucleons CM F o K 2 Short Range (tensor) Correlations in nuclei Hard Semi inclusive scattering A(e, e’p) Only 60-70% of the expected single-particle strength. SRC and LRC Hard inclusive scattering A(e, e’) This 20-25 % includes all three isotopic compositions (pn, pp, or nn) for the 2N-SRC phase in 12C. Hard exclusive scattering A(e, e’pp) and A(e, e’pn) Quasi-Free scattering off a nucleon in a short range correlated pair Hard exclusive triple – coincidence measurements proton proton experiment nuclei pairs Pmiss [MeV/c] EVA/BNL 12C pp only 300-600 E01-015/ 12C pp and np 300-600 Jlab E07-006/ 4He pp and np 400-850 JLab CLAS/JLab C, Al, Fe, Pb pp only 300-700 R. Subedi et al., Science 320, 1476 (2008). 12 BNL / EVA C 12C(e,e’pn) / 12C(e,e’p) [12C(e,e’pn) / 12C(e,e’pp)] / 2 [12C(e,e’pp) / 12C(e,e’p)] / 2 np / pp SRC pairs ratio c Al Fe Pb O. -

Re-Analysis of the World Data on the EMC Effect and Extrapolation to Nuclear Matter
University of New Hampshire University of New Hampshire Scholars' Repository Honors Theses and Capstones Student Scholarship Spring 2014 Re-analysis of the World Data on the EMC Effect and Extrapolation to Nuclear Matter Stacy E. Karthas University of New Hampshire - Main Campus Follow this and additional works at: https://scholars.unh.edu/honors Part of the Nuclear Commons Recommended Citation Karthas, Stacy E., "Re-analysis of the World Data on the EMC Effect and Extrapolation to Nuclear Matter" (2014). Honors Theses and Capstones. 184. https://scholars.unh.edu/honors/184 This Senior Honors Thesis is brought to you for free and open access by the Student Scholarship at University of New Hampshire Scholars' Repository. It has been accepted for inclusion in Honors Theses and Capstones by an authorized administrator of University of New Hampshire Scholars' Repository. For more information, please contact [email protected]. Re-analysis of the World Data on the EMC Effect and Extrapolation to Nuclear Matter Stacy E. Karthas May 15, 2014 Abstract The EMC effect has been investigated by physicists over the past 30 years since it was discovered at CERN. This effect shows that the internal nucleon structure varies when in the nuclear medium. Data from SLAC E139 and JLab E03 103 were studied with the Coulomb correction and directly compared. The Coulomb distortion had a greater impact on the JLab data due to slightly lower energies and different kinematics. The EMC ratio was found to have a dependence on a kinematic variable, , which was removed when Coulomb corrections were applied. The methodology was developed to apply Coulomb corrections, which had been neglected in the past, and to extrapolate to nuclear matter to compare to theory. -

The EMC Effect Cannot Be Explained by Conventional Nuclear Physics
"Beam in 30 minutes or it's free" [S. Kuhn, S. Strauch, J. Watson] [D. Dutta] [W. Brooks] [P. Bosted] John Arrington Argonne National Lab "The next seven years..." production ψ 1 - The EMC effect and related measurements 2 - Color Transparency 3 - Quark propagation 4 - J/ Nucleons in the Nuclear Environment Jefferson Lab User's Group Annual Meeting, June 18, 2004 Topic: Study of nucleons (hadrons, quarks) in nuclei "Beam in 30 minutes or it's free" John Arrington , matter is hadrons Argonne National Lab "The next seven years..." real world In the lab (GeV accelerators), matter is quarks In the How do nucleons interact with the nucleus? How do other (exotic?) hadrons interact with the nucleus? How do quarks interact with the nucleus? Nucleons in the Nuclear Environment Jefferson Lab User's Group Annual Meeting, June 18, 2004 Questions for JLab: Bigger question: Does QCD matter in the real world? [fm] r 2.5 r [fm] 2.0 two quarks two nucleons 1.5 Potential between potential between 1.0 0.5 ~1 fm 0 1.2 0.4 2.0 1.6 0.8 -0.4 -0.8 0 V(r) V(r) [GeV] 18 tons! times the coulomb 12 Two "Realms" of Nuclear Physics 1 GeV/cm = >10 attraction in hydrogen Matter consists of colorless bound states of QCD Strongly attractive at all distances: Quark interactions cancel at large distances, making the interactions of hadrons finite. Don't observe quarks, gluons, or color in traditional nuclear physics Quarks have been swept under a very heavy (18 ton) rug QCD land quarks + gluons color Real world nucleons + mesons strong interaction 8 5 JLAB12 2 neutron stars -

EMC Effect in Electron and Neutrino Scattering
EMC Effect in Electron and Neutrino Scattering Ian Cloet¨ (Argonne National Lab) Collaborators Wolfgang Bentz (Tokai Uni.) and Tony Thomas (JLab) May 31, 2007 1 / 25 Theme ❖ Theme ❖ EMC Effect ● Are nucleon properties modified by the nuclear medium? ❖ Hadronic Tensor ❖ Parton Model ✦ Of fundamental importance. ❖ Calculation ❖ NJL model ✦ Remains an open question. ❖ Nucleon ... ❖ Quark Dis. ❖ Finite Density ● Areas where medium modifications seem important: ❖ Nucleon Dis. ❖ Expressions ✦ Quenching of gA in-medium ❖ Nucleon Dis. 12C ❖ Nucleon Dis. 28Si ✦ Nuclear magnetic moments ❖ Quark Dis. 12C 4 ❖ EMC effect ✦ Nuclear Form Factors (e.g. He) ❖ EMC ratios 28Si ❖ EMC effect ν (¯ν) ● ❖ EMC ratios 27Al Most importantly nuclear structure functions, this is the ❖ Is there medium modification EMC effect. ❖ Polarized EMC ❖ Conclusions 2 / 25 EMC Effect ❖ Theme ❖ EMC Effect ❖ Hadronic Tensor ❖ Parton Model ❖ Calculation ❖ NJL model ❖ Nucleon ... ❖ Quark Dis. ❖ Finite Density ❖ Nucleon Dis. ❖ Expressions ❖ Nucleon Dis. 12C ❖ Nucleon Dis. 28Si ❖ Quark Dis. 12C ❖ EMC effect ❖ EMC ratios 28Si ❖ EMC effect ν (¯ν) ❖ EMC ratios 27Al ❖ Is there medium modification ❖ Polarized EMC ❖ Conclusions ● J. J. Aubert et al. [European Muon Collaboration], Phys. Lett. B 123, 275 (1983). 3 / 25 Hadronic Tensor ❖ Theme ❖ EMC Effect ● Bjorken limit and Callen-Gross relations ❖ Hadronic Tensor (e.g. F2 =2xF1) ❖ Parton Model ❖ Calculation ✦ 1 ❖ NJL model For J = 2 target ❖ Nucleon ... ε qλP σ ❖ P ·q PµPν 2 µνλσ 2 Quark Dis. Wµν = gµν + F (x ,Q ) i F (x ,Q ) q2 P ·q 2 A ν 3 A ❖ Finite Density “ ” − ❖ Nucleon Dis. ❖ Expressions ❖ Nucleon Dis. 12C ✦ ❖ Nucleon Dis. 28Si For arbitrary J (2 J +2 structure functions) 12 ⌊ ⌋ ❖ Quark Dis. -

EMC Effect, Short-Range Correlations in Nuclei and Neutron Stars
EMC Effect, Short-Range Correlations in nuclei and Neutron Stars Mark Strikman, Penn State University PANIC 11, July 28, 2011 Key questions relevant for high density cold nuclear matter in neutron stars: • Are nucleons good nuclear quasiparticles? Do nucleon momentum distributions make sense for k > mπ? yes - at least up to momenta ~ 500 MeV/c • Probability and structure of the short-range/ high momentum correlations in nuclei 20% in medium and heavy nuclei - mostly tensor pn correlations. I=1 << I=0 • What are the most important non-nucleonic degrees of freedom in nuclei? EMC effect - definite signal - but probes admixture on the scale ≤ 1% • Microscopic origin of intermediate and short-range nuclear forces Meson exchange models - serious problem with lack of enhancement of antiquarks in nuclei 2 Probability and structure of SRC in nuclei Questions: ☛ Probability of SRC? ☛ Isotopic structure ☛ Non-nucleonic components Dominant contribution for large k; 2N SRC: k1 ~k |p1|<pF universal (A-independent up to isospin effects) V(k) k2 ~ - k2 > kF k ~-k momentum dependence - singular V(k) |p2|<pF 2 Two nucleon SRC 2N SRC ρ 5ρ0 ∼ Connections to neutron stars: m n f a) I=1 nn correlations, 2 Short-range NN correlations . p 1 n b) admixture of protons in neutron (SRC) have densities ÷ p 1.7 fm 1 stars → I=0 sensitivity comparable to the density in ∼ p n the center of a nucleon - n c) multi-nucleon correlations drops of cold dense nuclear matter 3 ρ .17fm− 0 ∼ 3 A(e,e’) at x>1 is the simplest reaction to check dominance of 2N, 3N SRC and to measure absolute probability of SRC NUCLEAR PHYSICS Q2 Define x = A Close nucle2qo0mnA encounters x=1 is exact kinematic limit for all Q2 for the scattering off a free nucleon; Jeffersonx=2 (x=3)Lab may is exact have directlykinematic observed limit for short-range all Q2 for the nucleic scattering correlations, off a A=2(A=3) with densities systemsimilar (up toto those<1% correction at the heart due of to a nuclear neutron binding) star. -

Exploring the Role of Pions in the Nucleus Dave Gaskell Jefferson Lab PN12 - November 3, 2004
Exploring the Role of Pions in the Nucleus Dave Gaskell Jefferson Lab PN12 - November 3, 2004 • Nuclear forces and “excess” pions • The ambiguous experimental landscape -> DIS and Drell-Yan results -> (p,n) Reactions -> Pion electroproduction π • New Directions Pions as Constituents • QCD describes strong interactions at the most fundamental level – hadrons (nucleons) are made of quarks and gluons • However, cannot generate nucleon parton distributions from 3 quarks + Q2 evolution • A meson cloud is required to understand the structure of the nucleon – Nucleon axial current partially conserved – Ability to extract pion form factor from H(e,e’π+) – Asymmetry of nucleon sea -> d /u Charged Pion Form Factor from Pion Electroproduction • No “free pion” target -> extraction of pion form factor at large Q2 requires use of “virtual pion” content of the proton • Excellent agreement between π+e elastic data and p(e,e’π+)n Sea-Quark Asymmetry from Drell-Yan N (target) µ+ _ γ* x2 q x1 q p (beam) µ- • Fermilab E866 measured D-Y cross section ratios σ ( p + d) /σ ( p + p) • Extracted results for d − u favor pion cloud models J.C. Peng et al., Phys. Rev. D58, 092004 (1998) Pions in “Conventional” Nuclear Physics • Yukawa’s initial insight -> π as carrier of strong force has proved remarkably durable • Modern effective NN forces (Bonn, Argonne V-18) are significantly more complex, but the fundamental principle is the same – Employ additional mesons (ρ, etc.) – Form factors control pion contributions at short distances –3N interactions? • Effective NN forces work! – Green’s Function Monte Carlo calculations accurately reproduce nuclear properties up to 12C –Only limited by CPU • These effective theories predict that there should be “extra” virtual pions in the nucleus The Pion Excess and Pions in the Nucleus • Using either mean field calculations or detailed N-N forces one can calculate a “pion excess” -> A A N δnπ (k) = nπ (k) − nπ (k) • Friman et al. -
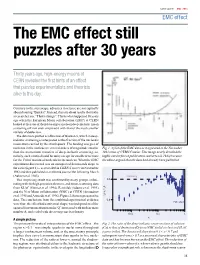
The EMC Effect Still Puzzles After 30 Years
CERN Courier May 2013 EMC effect Modulators, Power Supplies, RF Transmitters IPAC 2013 May 12 - 17 • Shanghai, China Visit us in Booth 11 The EMC effect still puzzles after 30 years ™ PowerMod Thirty years ago, high-energy muons at Solid-State Pulsed Power Systems CERN revealed the fi rst hints of an effect • Compact, Rugged, Reliable that puzzles experimentalists and theorists • Voltages to 500 kV alike to this day. Complete Turnkey Systems • Currents to 5 kA • Frequencies to Hundreds of kHz Contrary to the stereotype, advances in science are not typically • Hundreds of Installations Worldwide about shouting “Eureka!”. Instead, they are about results that make a researcher say, “That’s strange”. This is what happened 30 years ago when the European Muon collaboration (EMC) at CERN 35 Wiggins Avenue • Bedford, MA 01730 USA • www.divtecs.com looked at the ratio of their data on per-nucleon deep-inelastic muon scattering off iron and compared it with that of the much smaller nucleus of deuterium. The data were plotted as a function of Bjorken-x, which in deep- inelastic scattering is interpreted as the fraction of the nucleon’s momentum carried by the struck quark. The binding energies of nucleons in the nucleus are several orders of magnitude smaller Fig. 1. A plot of the EMC data as it appeared in the November than the momentum transfers of deep-inelastic scattering, so, 1982 issue of CERN Courier. This image nearly derailed the naively, such a ratio should be unity except for small corrections highly cited refereed publication (Aubert et al. 1983) because for the Fermi motion of nucleons in the nucleus. -

The EMC Effect and Nuclear Physics
The EMC Effect and Nuclear Physics: Current Status Aoibal Gattone Departamento de Física, CNEA. TANDAR Av. del Libertador 8250, U29 Buenos Aires. Argentina Abstract; The current experimental status and theoretical interpretations of the so-called EMC (European Muon Collaboration) effect are reviewed. A basic introduction to the origin of the effect is presented and a brief discussion of the data and its interpretation is given. The emphasis is placed on the different models that aim to explain the data, specifically those that invoke conventional nuclear physics (binding effects and pion dynamics) and the one which resorts to QCD arguments to justify a change in the confinement length scale. Also some recent developments will be commenced on. A few conclusions will be drawn as to the impact of the effect on traditional nuclear physics. 1. Introduction In this talk I will be discussing the structure functions describing the deep-inelastic lepton scattering off nuclear targets. The exact meaning of "structure functions" and "deep inelastic" will become clear later as the talk unfolds. To be more precise what we will be doing is comparing quark momentum distributions in nucleons and in nuclei. A common prejudice before 1983 (the year In which the EMC data came up) held that, in deep I Invited talk presented at the "Xa Reunião de Trabalho de Física Nuclear no Brasil", Caxambú, H. C, Brasil. 26-30 August 1987, -211- inelastic scattering a nucleus acts as an incoherent collection of free nucleons. The cross section per nucleon of a nucleus was therefore expected to be the same for all nuclei. -

First Measurement of Polarized EMC Effect for the Neutron December 5, 2005
(A New Letter-Of-Intent to Jefferson Lab PAC-29) First Measurement of Polarized EMC Effect for the Neutron December 5, 2005 X. Zheng1 Argonne National Laboratory, Argonne, IL 60439 A. Deur2 Jefferson Lab, Newport News, VA 23606 Abstract We propose to measure the EMC effect in polarized structure function for the neutron ¢¡¤£ at ¡ ¥§¦©¨ using a polarized He and a polarized Xe targets in Hall A. Results of this mea- surement would provide the first data on polarized EMC effect and important information for our understanding of the medium modification of nucleon spin structure. In this document, we first review the history and theories of the unpolarized EMC effect, and present existing calculations on the polarized EMC effect. Experimental design of the proposed measurement is presented in section 2 and a possible design for the new polarized Xe target is ¡¤£ described in section 3. Extractions of from He and Xe data are discussed in section 4. An analysis of all systematic and theoretical uncertainties is given in section 5. In section 6 we give the kinematics optimization and estimation of rates and statistical uncertainties for a polarized EMC measurement. We will then discuss possible physics impact and summarize the beam time ¡ ¡ request. Although we propose to use Xe, we will show that Ne is another possible nuclear target to use, which although requires more R&D effort, may provide similar or better statistical precision. Contents 1 The EMC Effect 4 1.1 Unpolarized EMC Effect – Data and Theories . 4 1.2 Theories for Polarized EMC Effect . 4 1.3 Polarized EMC Effect on the Neutron . -

In Medium Nucleon Structure Functions, SRC, and the EMC Effect
In Medium Nucleon Structure Functions, SRC, and the EMC effect Study the role played by high-momentum nucleons in nuclei A proposal to Jefferson Lab PAC 38, Aug. 2011 O. Hen (contact person), E. Piasetzky, I. Korover, J. Lichtenstadt, I. Pomerantz, I. Yaron, and R. Shneor Tel Aviv University, Tel Aviv, Israel M. Amarian, R. Bennett, G. Dodge, L.B. Weinstein (spokesperson) Old Dominion University, Norfolk, VA, USA G. Ron Hebrew University, Jerusalem, Israel W. Bertozzi, S. Gilad (spokesperson), A. Kelleher and V. Sulkosky Massachusetts Institute of Technology, Cambridge, MA, USA B.D. Anderson, A.R. Baldwin, and J.W. Watson Kent State University, Kent, OH, USA J.-O. Hansen, D.W. Higinbotham, M. Jones, S. Stepanyan, B. Sawatzky, and S. A. Wood (spokesperson), J. Zhang Thomas Jefferson National Accelerator Facility, Newport News, VA, USA G. Gilfoyle University of Richmond, Richmond, VA, USA P. Markowitz Florida International University, Miami, FL, USA A. Beck and S. Maytal-Beck Nuclear Research Center Negev, Beer-Sheva, Israel D. Day, C. Hanretty, R. Lindgren, and B. Norum University of Virginia, Charlottesville, VA, USA J. Annand, D. Hamilton, D. Ireland, K. Livingston, D. MacGregor, D. Protopopescu, and B. Seitz University of Glasgow, Glasgow, Scotland, UK 1 F. Benmokhtar Christopher Newport University, Newport News, VA, USA M. Mihovilovic and S. Sirca University of Ljubljana, Slovenia J. Arrington, K. Hafidi and X. Zhan Argonne National Lab, Argonne, IL, USA W.Brooks, and Hayk Hakobyan Universidad Técnica Federico Santa María Theoretical support: M. Sargsian Florida International University, Miami, FL, USA W. Cosyn, and J. Ryckebusch Ghent University, Ghent, Belgium G. -

Experimental Results on Nucleon Structure Lecture II
Experimental results on nucleon structure Lecture II Barbara Badelek University of Warsaw National Nuclear Physics Summer School 2013 Stony Brook University, July 15 – 26, 2013 Barbara Badelek (Univ. of Warsaw ) Experimental results on nucleon structure, II NNPSS 2013 1 / 86 Course literature Outline 1 Course literature 2 Introduction 3 Nucleon elastic form factors Basic formulae Form factor measurements Radiative corrections 4 Parton structure of the nucleon Feynman parton model Partons vs quarks Introducing gluons Parton distribution functions EMC effect Fragmentation functions Sum rules 5 “Forward” physics Phenomena at low x Diffraction Barbara Badelek (Univ. of Warsaw ) Experimental results on nucleon structure, II NNPSS 2013 2 / 86 Introduction Outline 1 Course literature 2 Introduction 3 Nucleon elastic form factors Basic formulae Form factor measurements Radiative corrections 4 Parton structure of the nucleon Feynman parton model Partons vs quarks Introducing gluons Parton distribution functions EMC effect Fragmentation functions Sum rules 5 “Forward” physics Phenomena at low x Diffraction Barbara Badelek (Univ. of Warsaw ) Experimental results on nucleon structure, II NNPSS 2013 3 / 86 Nucleon elastic form factors Outline 1 Course literature 2 Introduction 3 Nucleon elastic form factors Basic formulae Form factor measurements Radiative corrections 4 Parton structure of the nucleon Feynman parton model Partons vs quarks Introducing gluons Parton distribution functions EMC effect Fragmentation functions Sum rules 5 “Forward” physics