Fuzzy Mixed Integer Programming for Land Use Planning in Tumauini, Isabela Philippines
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

WFP Philippines Typhoon Rolly and Typhoon Ulysses Situation Report #3
WFP Philippines Typhoon Rolly and Typhoon Ulysses Situation Report #3 23 November 2020 Highlights In Numbers • WFP will provide cash assistance to more than 2,400 Over 2.3 million affected people across vulnerable households in Catanduanes. eight regions • WFP contributed to a rapid needs assessment in the Over 23,089 individuals displaced in most affected municipalities in the provinces of evacuation centres Isabela and Cagayan. Over 46,987 individuals displaced outside • WFP continues to provide logistics support to the evacuation centres Government, transporting 74,600 family food packs and 6,225 essential non-food items. WFP Response Typhoon Rolly and Typhoon Ulysses Situation Update Logistics • Just days after the onslaught of Typhoon Rolly (international name: Goni) on 1 November, Typhoon Ulysses (international name: Vamco) roughly crossed the same track and made landfall on 11 November. Rolly and Ulysses both left trails of destruction and affected millions of people in eight regions, hundreds of thousands of which remain displaced. • The death toll from Ulysses has risen to more than 70 and severely damages property and infrastructure. In Isabela and Cagayan provinces in the Cagayan Valley, heavy rains threatened to WFP loaned two generators to the Provincial Capitol of Catanduanes. They overspill Magat Dam, the largest in the country. will power a portable office for warehouse management, and the mobile Authorities released water from the dam to prevent it water filtration system to bring clean drinking water to communities whose water sources were damaged by the typhoon. Photo courtesy of Office of from spilling, but the surge from the opened Civil Defense – Jose Angelo Mangaoang floodgates submerged many houses. -

Executive Summary Comprehensive Land Use Plan (Clup)
EXECUTIVE SUMMARY COMPREHENSIVE LAND USE PLAN (CLUP) OF DELFIN ALBANO, ISABELA CY 2018-2027 I. Vision A Center of agro-industrial development in Northern Isabela with God-loving and empowered citizens living in a disaster-resilient community and ecologically-sound environment with integrated infrastructure support systems and vibrant economy led by responsive and transparent leadership. Mission To improve the quality of life for all residents of Delfin Albano by maximizing opportunities for social and economic development in order to become the agro-industrial center in Northern Isabela while retaining an attractive, sustainable and secure environment. II. Brief Situationer A. Physical Profile The municipality is composed of twenty-nine (29) barangays and seven sitios. Barangay Ragan Sur is the seat of Government that is centrally located along the Provincial / National Road from Ilagan and Mallig to Delfin Albano to Santo Tomas and Santa Maria this province. Delfin Albano has a total land area of 19,095.hectares. It is located some 35 kilometers, northwest of Ilagan, the capital town of the Province. It is bounded on the north by the municipality of Sto. Tomas, on the east by the municipality of Tumauini, the Cagayan River as the natural boundary, on the west by the municipalities of Quezon and Mallig and on the south by the municipalities of Quirino and Ilagan with Mallig River as natural boundary. Delfin Albano is subdivided into two (02) physiological areas namely the Eastern Area long the Cagayan River which is good for intensive agriculture and high density urban development as the western area along the mountain range which is good for intensive agriculture, pasture and forest purposes. -

Mobility and Sedentarization Among the Philippine Agta
SENRI ETHNOLOGICAL STUDIES 95: 119 –150 ©2017 Sedentarization among Nomadic Peoples in Asia and Africa Edited by Kazunobu Ikeya Mobility and Sedentarization among the Philippine Agta Tessa Minter Leiden University ABSTRACT This article provides an ethnography of Agta mobility, based on fieldwork in the northern Philippines conducted over the past decade. The Agta are a population of about 10,000 people, living in small settlements distributed along the coasts and in the mountainous interior of northeastern Luzon. They follow a hunting-fishing and gathering lifestyle, which includes a relatively mobile settlement pattern. First, this article aims to document Agta mobility by exploring its drivers and by showing how it is both facilitated and limited by kinship relations. How mobility varies regionally and seasonally will also be discussed. Second, the article focuses on Agta mobility in relation to Philippine development policies. This includes a discussion of past and recent efforts at sedentarization, as well as the government’s misconceptions of Agta mobility in relation to the ongoing ancestral land titling processes. Finally, the article explores the ongoing and future developments likely to influence Agta mobility. These concern Agta parents’ recent emphasis on enrolling their children in formal education and the approval of a road construction project that will traverse Agta living areas and the associated claims on coastal land by politically influential outsiders. An underlying question of this article is how anthropological knowledge on mobility could contribute to improving policy. INTRODUCTION Nomadism and sedentarization have long since raised the interest of policy makers, development practitioners and academics. Discussions have, however, focused mostly on pastoralist herders in arid and semi-arid regions of Eurasia and Africa (Khazanov and Wink 2001). -

Consolidated List of Establishments – Conduct of Cles
CONSOLIDATED LIST OF ESTABLISHMENTS – CONDUCT OF CLES 1. Our Lady of Victories Academy (OLOVA) Amulung, Cagayan 2. Reta Drug Solano, Nueva Vizcaya 3. SCMC/SMCA/SATO SM Cauayan City 4. GQ Barbershop SM Cauayan City 5. Quantum SM Cauayan City 6. McDonald SM Cauayan City 7. Star Appliance Center SM Cauyan City 8. Expressions Martone Cauyan City 9. Watch Central SM Cauayan City 10. Dickies SM Cauayan City 11. Jollibee SM Cauayan City 12. Ideal Vision SM Cauayan City 13. Mendrez SM Cauayan City 14. Plains and prints SM Cauayan City 15. Memo Express SM Cauayan City 16. Sony Experia SM Cauayan City 17. Sports Zone SM Cauayan City 18. KFC Phils. SM Cauayan City 19. Payless Shoe Souref SM Cauyan City 20. Super Value Inc.(SM Supermarket) SM Cauyan City 21. Watson Cauyan City 22. Gadget @ Xtreme SM Cauyan City 23. Game Xtreme SM Cauyan City 24. Lets Face II Cauyan City 25. Cafe Isabela Cauayan City 26. Eye and Optics SM Cauayan City 27. Giordano SM Cauayan City 28. Unisilver Cabatuan, Isabela 29. NAILAHOLICS Cabatuan, Isabela 30. Greenwich Cauayan City 31. Cullbry Cauayan City 32. AHPI Cauyan City 33. LGU Reina Mercedes Reina Mercedes, Isabela 34. EGB Construction Corp. Ilagan City 35. Cauayan United Enterp & Construction Cauayan City 36. CVDC Ilagan City 37. RRJ and MR. LEE Ilagan City 38. Savers Appliance Depot Northstar Mall Ilagan city 39. Jeffmond Shoes Northstar Mall Ilagan city 40. B Club Boutique Northstar Mall Ilagan city 41. Pandayan Bookshop Inc. Northstar Mall Ilagan city 42. Bibbo Shoes Northstar Mall Ilagan city 43. -

2016 Annual Accomplishment Report
MINERAL RESOURCES MANAGEMENT DIVISION 1. Processing and Issuance of Permits Commercial Sand and Gravel (CSAG) – this office received and processed Fifty Five (55) CSAG Permit Applications from the different quarry locations within the province with corresponding administrative/processing fees collected by the Provincial Treasurer’s Office amounting to Six Hundred Twenty Three Thousand One Hundred Fifty Pesos (Php623, 150.00). List of CSAG Permit Applications Received: QUARRY LOCATION NAME Barangay Municipality 1 Rosalino U. Urandayan San Ignacio City of Ilagan Jones Chapter Guardians Savings & Credit 2 Barangay 2 Jones Cooperative 3 Arnold S. Ferrer Carpintero Tumauini 4 Western Pinacanauan Development Cooperative Alinguigan 2nd City of Ilagan 5 Edwin P. Uy Furao Gamu 6 Edwin P. Uy Banquero Reina Mercedes 7 Degullacion A. Cabbab Zone II & Zone III San Mariano 8 Carlos Clyde U. Chan Upi Gamu 9 Carlito M. Uy Lenzon Gamu 10 Raul T. Sawit Saranay Cabatuan 11 Flordeliza M. Balisi Baculod City of ilagan 12 Eleodoro D. Bermudez, Jr. Aggassian City Of Ilagan 13 CTR Enterprises Turod Reina Mercedes 14 AC&C builders & Ent. c/o Alvin D. Uy Santiago Reina Mercedes 15 A1 & A2 Multi-purpose Cooperative c/o Jose B. Gangan Alinguigan 1st and 2nd City of Ilagan 16 Christopher B. Uy Sta. Visitacion Tumauini 17 Dutch Anne V. Uy Carpintero Tumauini 18 Allan C. Malayao Annanuman San Pablo Flow of Pari-ir Development Cooperative c/o 19 Saranay Cabatuan Norlando T. Manibog 20 Glenn Moore Angelo E. Caramancion Disimpit Jones Cabisera 8(Sta. 21 Christopher E. Maltu City Of Ilagan Maria) 22 Cinderella M. Gatan Casibarag Sur Cabagan Camarunggayan and 23 Aurora Employees Multi-Purpose Cooperative Aurora Panecien 24 Felino C. -

Province, City, Municipality Total and Barangay Population BATANES
2010 Census of Population and Housing Batanes Total Population by Province, City, Municipality and Barangay: as of May 1, 2010 Province, City, Municipality Total and Barangay Population BATANES 16,604 BASCO (Capital) 7,907 Ihubok II (Kayvaluganan) 2,103 Ihubok I (Kaychanarianan) 1,665 San Antonio 1,772 San Joaquin 392 Chanarian 334 Kayhuvokan 1,641 ITBAYAT 2,988 Raele 442 San Rafael (Idiang) 789 Santa Lucia (Kauhauhasan) 478 Santa Maria (Marapuy) 438 Santa Rosa (Kaynatuan) 841 IVANA 1,249 Radiwan 368 Salagao 319 San Vicente (Igang) 230 Tuhel (Pob.) 332 MAHATAO 1,583 Hanib 372 Kaumbakan 483 Panatayan 416 Uvoy (Pob.) 312 SABTANG 1,637 Chavayan 169 Malakdang (Pob.) 245 Nakanmuan 134 Savidug 190 Sinakan (Pob.) 552 Sumnanga 347 National Statistics Office 1 2010 Census of Population and Housing Batanes Total Population by Province, City, Municipality and Barangay: as of May 1, 2010 Province, City, Municipality Total and Barangay Population UYUGAN 1,240 Kayvaluganan (Pob.) 324 Imnajbu 159 Itbud 463 Kayuganan (Pob.) 294 National Statistics Office 2 2010 Census of Population and Housing Cagayan Total Population by Province, City, Municipality and Barangay: as of May 1, 2010 Province, City, Municipality Total and Barangay Population CAGAYAN 1,124,773 ABULUG 30,675 Alinunu 1,269 Bagu 1,774 Banguian 1,778 Calog Norte 934 Calog Sur 2,309 Canayun 1,328 Centro (Pob.) 2,400 Dana-Ili 1,201 Guiddam 3,084 Libertad 3,219 Lucban 2,646 Pinili 683 Santa Filomena 1,053 Santo Tomas 884 Siguiran 1,258 Simayung 1,321 Sirit 792 San Agustin 771 San Julian 627 Santa -

HISTORICAL DEVELOPMENT of the MUNICIPALITY of SAN PABLO, ISABELA Philippine Copyright © 15 January 2018
Republic of the Philippines Province of Isabela ISABELA TOURISM OFFICE HISTORICAL DEVELOPMENT OF THE MUNICIPALITY OF SAN PABLO, ISABELA Philippine Copyright © 15 January 2018 In recorded history, the oldest existing pueblo of the Province of Isabela since its foundation up to present time is the town of San Pablo. The territory of what is now the Municipality of San Pablo, Isabela was originally incorporated in the territory then known as La Irraya. Irraya (Addaya and Yrraya in other manuscripts) region comprised the vast area from Tuguegarao in Cagayan province up to the present Gamu town in Isabela province. Irraya was also the term used for the native’s name and their dialect. Irraya is an Ibanag word which means “upriver”. In the Gaddang dialect, the term “dirraya” also means “upriver”. In 1607, the provincial chapter of the Holy Rosary Province (or Dominicans) ordered Frays Luis Flores and Francisco Minaio to the Irraya speaking Pilitan (now a barangay of Tumauini town) and its adjoining communities, to exert all efforts that the natives must learn to speak Ibanag and to minister to them in the said language. In short, Ibanag (Ybanag) was made the official language in the valley. Ultimately, the distinct Irraya area, its people and the dialect became extinct with the whole area, its residents and tongue now known in the modern world as Ibanag. Only a handful from barangays Tallag and San Bernardo in Cabagan town can still remember some Irraya phrases. As a result of the historic Irraya Revolt on November 8, 1621, a new town was organized by Dominican missionary, Fray Pedro de Santo Tomas, gathering the Irrayas from the former Christian missions of Pilitan, Abbuatan, Bolo and Batavag and named it “Maquila” which was situated at the junction of the Cagayan and Pinacanauan Rivers of Tuguegarao. -

History of Cauayan City
Republic of the Philippines Province of Isabela ISABELA TOURISM OFFICE HISTORICAL DEVELOPMENT OF CITY OF CAUAYAN PROVINCE OF ISABELA Philippine Copyright 2014 September 8 http://cityofcauayan.gov.ph/index.php/city-profile/history PRE-SPANISH SETTLERS In the beginning, the land now known as Cauayan City in the mid-southern part of the Province of Isabela in Cagayan Valley Region in Northern Philippines, was first roamed and settled by dark skinned and kinky haired pygmies who arrived in the island of Luzon during the Stone Age about 25,999 years ago. The Negrito Atta (Aeta) peoples of modern times were relatives of the first settlers of northeast Luzon. Between 200 B.C. and 300 A.D., colonizing expeditions of Indo-Malay peoples, the forefathers of the founders of Cauayan, arrived along the northern coast of Luzon. The Gaddang people were one of the many Indo-Malay tribes. They found the Cagayan River watershed sparsely occupied by long-established Aeta, while the hills were already populated by the more-recently arrived Igorot (thought to originate from Taiwan as late as 500 B.C.). The Indo-Malay colonists practiced swidden (slash-and-burn based shifting cultivation) farming, and developed successful littoral and riparian societies as well; all economies which demand low population density. Whenever there were population increases following economic success or continued in-migration, the Indo-Malays were forced to move. Over many generations they spread inland along the Cagayan River and its tributaries. As Gaddangs occupy lands further away from the mouth of the river than most Indo-Malay groups, they may be considered likely to have been among the earliest to arrive. -

Assessment of Heritage Churches in Isabela, Cagayan Valley
International Journal of Scientific Engineering and Research (IJSER) ISSN (Online): 2347-3878 Index Copernicus Value (2015): 56.67 | Impact Factor (2017): 5.156 Assessment of Heritage Churches in Isabela, Cagayan Valley Susan C. Vallejo College of Engineering, Architecture & Technology, Isabela State University, Ilagan, Philippines Abstract: This study focused on the assessment of the present condition of the five (5) heritage churches in Isabela namely: San Pablo de Cabigan Church of San Pablo, St. Rose of Lima Parish of Gamu, St. Matthias Parish Church of Tumauini, Our Lady of Atocha Church of Alicia and Our Lady of the Pilar Church in Cauayan City. Ocular inspections and observations were performed to determine the structural defects, the non-structural defects and damages of the structures. The compressive strengths of these churches were determined by the non-destructive method through rebound hammer. It also includes the profile of the churches and the relationships between the ages of the churches to its compressive strengths were determined. Findings showed that San Pablo de Cabigan Church located at Cabagan is the oldest church while the youngest church is Our Lady of Atocha at Alicia, Isabela. Moreover, Our Lady of Pillar Parish Church at Cauayan is the largest church in terms of floor area while the smallest is Our Lady of Atocha Parish Church at Alicia, Isabela. Majority of the churches used bricks as building materials. The existences of cracks on walls of the churches were visible which caused the damaged of the structure. Moreover, the non-structural defects such as botanical growth, timber decay, human error and damaged stone details contributed to the deterioration of the building. -

Illegal Logging in the Northern Sierra Madre Natural Park, the Philippines
[Downloaded free from http://www.conservationandsociety.org on Friday, January 13, 2012, IP: 129.79.203.177] || Click here to download free Android application for this journal Conservation and Society 9(3): 202-215, 2011 Article Illegal Logging in the Northern Sierra Madre Natural Park, the Philippines Jan van der Ploega,#, Merlijn van Weerdb, Andres B. Masipiqueñac and Gerard A. Persoona aInstitute of Cultural Anthropology and Development Sociology, Leiden University, the Netherlands bInstitute of Environmental Sciences, Leiden University, the Netherlands cCollege of Forestry and Environmental Management, Isabela State University, the Philippines #Corresponding author. E-mail: [email protected] Abstract Illegal logging is a threat to biodiversity and rural livelihoods in the Northern Sierra Madre Natural Park, the largest protected area in the Philippines. Every year between 20,000 and 35,000 cu. m wood is extracted from the park. The forestry service and municipal governments tolerate illegal logging in the protected area; government offi cials argue that banning an important livelihood activity of households along the forest frontier will aggravate rural poverty. However this reasoning underestimates the scale of timber extraction, and masks resource capture and collusive corruption. Illegal logging in fact forms an obstacle for sustainable rural development in and around the protected area by destroying ecosystems, distorting markets, and subverting the rule of law. Strengthening law enforcement and controlling corruption are prerequisites for sustainable forest management in and around protected areas in insular southeast Asia. Keywords: illegal logging, law enforcement, corruption, poverty, Northern Sierra Madre Natural Park, Philippines INTRODUCTION the Philippine forest frontier (National Statistical Coordination Board 2007). -

Order, ERC Case No. 2016-085 RC
IN THE MATTER OF THE APPLICATION FOR THE APPROVAL OF THE POWER SUPPLY AGREEMENT(PSA) BETWEEN ISABELA II ELECTRIC COOPERATIVE, INC. (ISELCO II) AND ANDA POWER CORPORATION (ANDA) ERC CASE NO. 2016-085 RC ORDER On 29 April 2016, Isabela II Electric Cooperative, Inc. (ISELCO II) and Anda Power Corporation (ANDA) filed their Application for approval oftheir Power Supply Agreement (PSA). In support of said Application, ISELCO II and ANDA alleged, among others, the following: 1. Joint Applicant ISELCO II is an electric cooperative duly organized and existing under Philippine law, with principal office at Brgy. Alibagu, Hagan City, Isabela. It was granted an exclusive franchise issued by the National Electrification Commission (NEC) to operate an electric light and power distribution service in the City of Hagan and the following municipalities in Isabela: Aurora, Benito Soliven, Burgos, Cabagan, Delfin Albano, Gamu, Mallig, Nagui.lian, Quezon, Quirina, Roxas, San Manu;!, d San Pablo, Sta. Maria, San Mariano, Sto. Tom/ f ERC CASE NO. 2016-085 RC Order/5 August 2016 Page 2 of 14 Tumauini, Divilacan, Maconacon, Palanan, and Dinapigue; the coastal towns of Divilacan and Maconacon were however waived for a Qualified Third Party (QTP). 2. Joint Applicant ANDA is a power generation company duly organized under Philippine law, with principal office address at TECO Special Economic Zone, Bo. Bundagul, Mabalacat, Pampanga. Copy of ANDA's Articles of Incorporation, Certificate of Incorporation and latest General Information Sheet are attached to the Application as Annexes "A", "B" and "C", respectively; 3. Applicants may be served with orders and other processes of the Commission through respective counsels; NATURE AND SCOPE OF THE APPLICATION 4. -
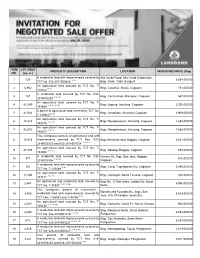
(Php) 1 339 a Residential Land with Improvements Cover
ITEM LOT AREA PROPERTY DESCRIPTION LOCATION INDICATIVE PRICE (Php) NO. (sq. m.) A residential land with improvements covered by Alta Verde Road, Alta Verde Subdivision, 1 339 3,668,000.00 TCT No. 016-2011000826 1/ 4/ Brgy. Irisan, Tuba, Benguet An agricultural land covered by TCT No. T- 2 6,952 Brgy. Calantac, Alcala, Cagayan 731,000.00 140462 5/ 8/ A residential land covered by TCT No. 034- 3 167 Brgy. Centro East, Allacapan, Cagayan 367,000.00 2018000267 3/ 4/ 12/ An agricultural land covered by TCT No. T- 4 83,340 Brgy. Logung, Amulung, Cagayan 2,500,000.00 141699 2/ 4/ 8/ 12/ 15/ A parcel of agricultural land covered by TCT No. 5 41,563 Brgy. Annafatan, Amulung, Cagayan 2,909,000.00 T-140920 5/ 12/ An agricultural land covered by TCT No. T- 6 42,212 Brgy. Nangalasauan, Amulung, Cagayan 1,688,000.00 140916 1/ 5/ 12/ An agricultural land covered by TCT No. T- 7 42,212 Brgy. Nangalasauan, Amulung, Cagayan 1,688,000.00 140917 1/ 5/ 12/ Two contiguous parcels of agricultural land with 8 10,918 improvements covered by TCT Nos. 032- Brgy.Hacienda-Intal, Baggao, Cagayan 5,631,000.00 2018003553 and 032-2018003554 2/ 4/ 12/ An agricultural land covered by TCT No. T- 9 27,768 Brgy. Adaoag, Baggao, Cagayan 833,000.00 143040 2/ 5/ 12/ A residential land covered by TCT No. 032- Herrero St., Brgy. San Jose, Baggao, 10 371 816,000.00 2018003556 1/ 4/ 12/ Cagayan A residential land with improvements covered by 11 301 Brgy.