Evaluating NBA Shooting Ability Using Shot Location
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Colby Trojans Lose Close One to Dodge City
FREE PRE ss Page 8 Colby Free Press Thursday, January 14, 2010 SSPORTPORT SS Colby Trojans Bulldogs’ senior lose close one selected for team By Judy Rogers Midway Café, Schiltz Harvesting, Golden Plains High School and my family for their financial judyusd316.org support that helps give me the opportunity to play,” she said. to Dodge City Golden Plains senior Jenna “Thanks also to Orba Smith, my Bruggeman has been chosen to volleyball coach throughout high By Andy Heintz omore Aireus Stephenson sparked play in the Northwest Kansas All- school, for helping me earn this Colby Free Press Colby’s rally. Michelson made Star volleyball game at 4 p.m. honor.” [email protected] several buckets inside the lane and Sunday at the Colby Community “I’m very pleased that Jenna Stephenson hit a three and scored Building. was selected to play in the North- The Trojans men’s basketball on a tough drive. The Trojans “It is an honor to be selected to west Kansas All-Star Volleyball team mounted a fierce rally that trailed 57-47 with 8:36 left. play in this event,” said Brugge- Match,” said Smith. “Throughout almost erased a 17-point deficit Stephenson penetrated down man. “I hope many volleyball fans the 2009 volleyball season, Jenna in the second half Wednesday, but the lane and hit Morris with a nice will come to enjoy these match- exhibited a positive attitude, an they were unable to get over the bounce pass inside that allowed es.” exemplary work ethic, as well as hump and beat Dodge City. -

Rosters Set for 2014-15 Nba Regular Season
ROSTERS SET FOR 2014-15 NBA REGULAR SEASON NEW YORK, Oct. 27, 2014 – Following are the opening day rosters for Kia NBA Tip-Off ‘14. The season begins Tuesday with three games: ATLANTA BOSTON BROOKLYN CHARLOTTE CHICAGO Pero Antic Brandon Bass Alan Anderson Bismack Biyombo Cameron Bairstow Kent Bazemore Avery Bradley Bojan Bogdanovic PJ Hairston Aaron Brooks DeMarre Carroll Jeff Green Kevin Garnett Gerald Henderson Mike Dunleavy Al Horford Kelly Olynyk Jorge Gutierrez Al Jefferson Pau Gasol John Jenkins Phil Pressey Jarrett Jack Michael Kidd-Gilchrist Taj Gibson Shelvin Mack Rajon Rondo Joe Johnson Jason Maxiell Kirk Hinrich Paul Millsap Marcus Smart Jerome Jordan Gary Neal Doug McDermott Mike Muscala Jared Sullinger Sergey Karasev Jannero Pargo Nikola Mirotic Adreian Payne Marcus Thornton Andrei Kirilenko Brian Roberts Nazr Mohammed Dennis Schroder Evan Turner Brook Lopez Lance Stephenson E'Twaun Moore Mike Scott Gerald Wallace Mason Plumlee Kemba Walker Joakim Noah Thabo Sefolosha James Young Mirza Teletovic Marvin Williams Derrick Rose Jeff Teague Tyler Zeller Deron Williams Cody Zeller Tony Snell INACTIVE LIST Elton Brand Vitor Faverani Markel Brown Jeffery Taylor Jimmy Butler Kyle Korver Dwight Powell Cory Jefferson Noah Vonleh CLEVELAND DALLAS DENVER DETROIT GOLDEN STATE Matthew Dellavedova Al-Farouq Aminu Arron Afflalo Joel Anthony Leandro Barbosa Joe Harris Tyson Chandler Darrell Arthur D.J. Augustin Harrison Barnes Brendan Haywood Jae Crowder Wilson Chandler Caron Butler Andrew Bogut Kentavious Caldwell- Kyrie Irving Monta Ellis -

Issue 4 BASKETBALL RETIRED PLAYERSBASKETBALL RETIRED PLAYERS ASSOCIATION ASSOCIATION the OFFICIAL MAGAZINE of the NATIONAL CONTENTS
WE’RE PROUD TO SUPPORT THE NATIONAL BASKETBALL RETIRED PLAYERS ASSOCIATION Being Chicago’s Bank™ means doing our part to give back to the local charities and social organizations that unite and strengthen our communities. We’re particularly proud to support the National Basketball Retired Players Association and its dedication to assisting former NBA, ABA, Harlem Globetrotters, and WNBA players in their CHICAGO’S BANK TM transition from the playing court into life after the game, while also wintrust.com positively impacting communities and youth through basketball. Banking products provided by Wintrust Financial Corp. Banks. LEGENDS Issue 4 BASKETBALL RETIRED PLAYERS ASSOCIATION ASSOCIATION BASKETBALL RETIRED PLAYERS BASKETBALL RETIRED PLAYERS THE OFFICIAL MAGAZINE CONTENTS of the NATIONAL KNUCKLEHEADS PODCAST NATIONAL HOMECOMING: p.34 TWO PEAS JUWAN HOWARD IS p.2 PROUD AND A POD BACK AT MICHIGAN In Partnership with The Players’ Tribune, the Ready to bring NBA swagger to the storied Knuckleheads Podcast Has Become a Hit with program where he once played PARTNER Fans and Insiders Alike. TABLE OF CONTENTS THE KNUCKLEHEADS PODCAST p.2 TWO PEAS AND A POD OF THE KEYON DOOLING NANCY LIEBERMAN p.6 BEYOND THE COURT p.30 POWER FORWARD 2019 LEGENDS CONFERENCE p.11 WOMEN OF INFLUENCE SUMMIT PUTS BY NANCY LIEBERMAN SPOTLIGHT ON OPPORTUNITY p.12 NBRPA HOSTS ‘BRIDGING THE GAP’ NBA AND It’s a great time to be a female in the SUMMIT CONNECTING CURRENT AND game of basketball. FORMER PLAYERS p.13 BUSINESS AFTER BASKETBALL NBRPA. p.14 THE FUTURE IS FRANCHISING “IT’S ABOUT GOOD VIBES, p.15 HAIRSTYLES ON THE HARDWOOD NOT CONCENTRATING ON FAREWELL, ORACLE ARENA ANYTHING NEGATIVE. -

Issue 2 BASKETBALL RETIRED PLAYERS RETIRED PLAYERSBASKETBALL BASKETBALL ASSOCIATION ASSOCIATION the OFFICIAL MAGAZINE of the NATIONAL CONTENTS
PROUD PARTNER OF THE NBA AND NBRPA. MGMRESORTS.COM LEGENDS Vol. 1, Issue 2 BASKETBALL RETIRED PLAYERS ASSOCIATION ASSOCIATION BASKETBALLBASKETBALL RETIRED PLAYERS RETIRED PLAYERS MAGAZINE THE OFFICIAL CONTENTS of the NATIONAL JAMAL MASHBURN NATIONAL NBA Legend The NBA Biography p. 8 ON TRACK WOMEN WINNING IN For Jamal Mashburn, Retirement From The NBA p. 2 Was Just The Beginning BUSINESS Basketball and business were “parallel dreams” for Legends of the WNBA reach new heights on and Jamal Mashburn. Every step of his journey had to off the court. further both ambitions. Never stop learning on the court, in the classroom and, most of all, in everyday life. Never stop aspiring. NANCY LIEBERMAN MAKING p. 32 HISTORY Nancy Lieberman Becomes First Female Coach To Win Professional Men’s Basketball JAYSON WILLIAMS Championship. p. 20 GETS THE REBOUND Former NBA All-Star Finds Fulfi llment through Treatment and Wellness Venture. TABLE OF CONTENTS LEGENDS IN BUSINESS p. 2 JAMAL MASHBURN IS ON TRACK p. 8 WOMEN WINNING IN BUSINESS p. 13 THE ART OF SELLING FINDING HOPE p. 14 WHO’S YOUR FINANCIAL GENERAL MANAGER? p. 28 THROUGH HUMILITY THE TRANSITION TO LIFE AFTER BASKETBALL ADVICE FROM NBA p. 20 JAYSON WILLIAMS ON MENTAL HEALTH ALLSTAR, OLYMPIAN & ASSISTANT COACH p. 28 FINDING HOPE THROUGH HUMILITY VIN BAKER WHERE ARE THEY NOW? p. 16 THE LEGACY OF SHERYL SWOOPES A look back at Vin Baker’s incredible career and his rise back to the Bucks. p. 18 BUSINESS FOUNDER & CHAIRMAN CHOO SMITH p. 36 HALL OF FAME 2018 p. 1 p. 2 THE OFFICIAL MAGAZINE of the NATIONAL BASKETBALL RETIRED PLAYERS ASSOCIATION LEGENDS Vol. -

Dynamic Player Significance (DPS): a New Comprehensive Basketball Statistic
Dynamic Player Significance (DPS): A new comprehensive basketball statistic David Hill Media Lab, Massachusetts Institute of Technology Cambridge, Massachusetts, USA [email protected] 15.071 (The Analytics Edge) Final Project May 13, 2013 Abstract Dynamic player significance is a new basketball metric designed to measure each NBA player's importance, or significance, to his franchise. This metric attempts to clearly define each player's role on the team and how it fits with the team's identity. Its key aspect is that it is influenced by the on-court identity of each franchise, which is defined as the collection of factors that contribute most to a win by a given team. These factors differ for every NBA team. Therefore, two players with completely identical stats/skillsets, but different teams, will most likely have different significance values. Alternatively, if a player is traded from one team to another, his significance will differ on the new team even if his production remains constant. Hence, dynamic player significance. Here, I have broken down the components of the model and explored three case studies that clearly show how teams’ identities deviate. Additionally, player evaluations have been explored to show tendencies in the model across multiple conditions. The proposed statistic could help inform team personnel decisions and coaching strategies, in addition to gauging player effectiveness. Motivation In the NBA, one of the most important things for any team to establish is an identity. These are the traits that define a team. Often, identity is the major factor that governs all transactions, whether the team is looking for players, hiring a coach, or filling front office positions. -

Hr9065-00 Page 1 of 2 House Resolution 1 A
FLORIDA HOUSE OF REP RESENTATIVE S HR 9065 2014 1 House Resolution 2 A resolution congratulating the Miami Heat Basketball 3 Team for winning its third National Basketball 4 Association Championship. 5 6 WHEREAS, on June 20, 2013, the Miami Heat won its third 7 National Basketball Association (NBA) Championship by defeating 8 the San Antonio Spurs at Miami, with a score of 95-88, in the 9 seventh game of the NBA Finals, and 10 WHEREAS, former Head Coach and current team president Pat 11 Riley led the team to its first championship in 2006, and 12 current Head Coach Erik Spoelstra led the team to back-to-back 13 championships in 2012 and 2013, and 14 WHEREAS, the Miami Heat entered the NBA as an expansion 15 franchise in the 1988-1989 season and has since won three NBA 16 Championships, four Eastern Conference Championships, and ten 17 division titles and has made a total of 17 playoff appearances, 18 and 19 WHEREAS, under the exemplary leadership of its coaching 20 staff, the Miami Heat, including LeBron James, Dwayne Wade, 21 Chris Bosh, Ray Allen, Chris Andersen, Joel Anthony, Shane 22 Battier, Mario Chalmers, Norris Cole, Udonis Haslem, Juwan 23 Howard, James Jones, Rashard Lewis, Mike Miller, and Jarvis 24 Varnado, united to form the 2013 championship team, and Page 1 of 2 hr9065-00 FLORIDA HOUSE OF REP RESENTATIVE S HR 9065 2014 25 WHEREAS, the Miami Heat's contributions extend well beyond 26 the basketball court, as the organization has grown to become an 27 integral part of the South Florida community through its public 28 service -

A Descriptive Model for NBA Player Ratings Using Shot-Specific-Distance Expected Value Points Per Possession
A Descriptive Model for NBA Player Ratings Using Shot-Specific-Distance Expected Value Points per Possession Chris Pickard MCS 100 June 5, 2016 Abstract This paper develops a player evaluation framework that measures the expected points per possession by shot distance for a given player while on the court as either an offensive or defensive adversary. This is done by modeling a basketball possession as a binary progression of events with known expected point values for each event progression. For a given player, the expected points contributed are determined by the skills of his teammates, opponents and the likelihood a particular event occurs while he is on the court. This framework assesses the impact a player has on his team in terms of total possession and shot-specific-distance offensive and defensive expected points contributed per possession. By refining the model by shot-specific-distance events, the relative strengths and weaknesses of a player can be determined to better understand where he maximizes or minimizes his team’s success. In addition, the model’s framework can be used to estimate the number of wins contributed by a player above a replacement level player. This can be used to estimate a player’s impact on winning games and indicate if his on-court value is reflected by his market value. 1 Introduction In any sport, evaluating the performance impact of a given player towards his or her team’s chance of winning begins by identifying key performance indicators [KPIs] of winning games. The identification of KPIs begins by observing the flow and subsequent interactions that define a game. -

Atelier: Mathematics in English
Atelier: Mathematics in English Part 4: A player's performance during a season You now have a method to evaluate a player's performance. How could you use this to evaluate a team's performance ? 2013 NBA Finals : The Miami Heat won the chamionship . Miami Heat : San Antonio Spurs : Player Points FG% Rebounds Assists Player Points FG% Rebounds Assists LeBron James 25.3 .447 10.9 7.0 Tim Duncan 18.9 .490 12.1 1.4 Dwyane Wade 19.6 .476 4.0 4.6 Tony Parker 15.7 .412 1.9 6.4 Chris Bosh 11.9 .462 8.9 2.1 Kawhi Leonard 14.6 .513 11.1 0.9 Ray Allen 10.6 .543 2.3 1.6 Danny Green 14.0 .444 4.1 0.7 Mario Chalmers 10.6 .388 2.7 2.1 Manu Ginobili 11.6 .433 2.1 4.3 Gary Neal 9.4 .414 2.4 0.9 Shane Battier 5.6 .444 1.6 0.9 Tiago Splitter 4.9 .448 2.0 0.4 Mike Miller 5.3 .591 2.7 0.9 Boris Diaw 4.0 .500 2.5 1.7 Chris Andersen 4.4 .727 3.0 0.0 DeJuan Blair 3.7 .455 2.7 0.3 Norris Cole 3.0 .273 1.0 2.4 Matt Bonner 1.8 .400 1.2 0.2 Udonis Haslem 1.5 .444 2.8 0.0 Cory Joseph 1.8 .444 1.0 1.0 James Jones 2.0 .400 0.3 0.0 Patrick Mills 2.0 .400 0.5 0.0 Rashard Lewis 1.3 .333 0.7 0.7 Nando De Colo 0.0 0.5 0.5 Joel Anthony 0.5 .500 1.8 0.0 Tracy McGrady 0.0 .000 2.0 2.5 Team Totals 97.0 .459 39.7 21.1 Team Totals 97.7 .451 41.9 18.4 2014 NBA Finals : The San Antonion Spurs won the championship . -
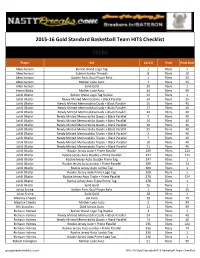
2015-16 Gold Standard Basketball Checklist;
2015-16 Gold Standard Basketball Team HITS Checklist 76ERS Player Set Card # Team Print Run Allen Iverson Bullion Brand Logo Tag 1 76ers 1 Allen Iverson Golden Jumbo Threads 8 76ers 10 Allen Iverson Golden Pairs Dual Player Relic 1 76ers 25 Allen Iverson Mother Lode Auto 7 76ers 35 Allen Iverson Solid Gold 20 76ers 1 Henry Bibby Mother Lode Auto 24 76ers 99 Jahlil Okafor Bullion Brand Logo Tag Rookie 13 76ers 1 Jahlil Okafor Newly Minted Memorabilia + Black Parallel 24 76ers 25 Jahlil Okafor Newly Minted Memorabilia Duals + Black Parallel 15 76ers 40 Jahlil Okafor Newly Minted Memorabilia Duals + Black Parallel 17 76ers 40 Jahlil Okafor Newly Minted Memorabilia Duals + Black Parallel 24 76ers 40 Jahlil Okafor Newly Minted Memorabilia Quads + Black Parallel 9 76ers 40 Jahlil Okafor Newly Minted Memorabilia Quads + Black Parallel 14 76ers 40 Jahlil Okafor Newly Minted Memorabilia Quads + Black Parallel 20 76ers 40 Jahlil Okafor Newly Minted Memorabilia Quads + Black Parallel 25 76ers 40 Jahlil Okafor Newly Minted Memorabilia Triples + Black Parallel 2 76ers 40 Jahlil Okafor Newly Minted Memorabilia Triples + Black Parallel 7 76ers 40 Jahlil Okafor Newly Minted Memorabilia Triples + Black Parallel 10 76ers 40 Jahlil Okafor Newly Minted Memorabilia Triples + Black Parallel 11 76ers 40 Jahlil Okafor Rookie Jersey Auto + Prime Parallel 209 76ers 224 Jahlil Okafor Rookie Jersey Auto Double + Prime Parallel 247 76ers 174 Jahlil Okafor Rookie Jersey Auto Double Prime Tag 247 76ers 1 Jahlil Okafor Rookie Jersey Auto Jumbo + Prime Parallel 309 76ers -

A Complete Breakdown of Every NBA Player's Salary, Where They
$1,422,720 (DonatasMotiejunas,Houston) $3,526,440 (JonasValanciunas,Toronto) Lithuania: $4,949,160 $12,350,000 (SergeIbaka,OklahomaCity) $3,049,920 (BismackBiyombo,Charlotte) Congo: $15,399,920 Total Salaries of Players that Schools Produced in Millions of US Dollars 100M 120M 140M 160M 180M 200M NBA Salary Distribution by Country that Produced Players SalaryDistributionbyCountrythatProduced NBA 20M 40M 60M 80M 947,907 (OmriCasspi,Houston) Israel: $947,907 0M 3 $10,105,855 |Gerald Wallace, Boston $3,250,000 |Alonzo Gee, Cleveland $2,652,000 |Mo Williams, Portland $3,135,000 |Jerryd Bayless, Boston Arizona $1,246,680 |Solomon Hill, Indiana $12,868,632 |Andre Iguodala, Golden State $3,500,000 |Jordan Hill, LA Lakers 10 $6,400,000 |Channing Frye Phoenix $5,625,313 |Jason Terry, Sacramento $5,016,960 |Derrick Williams, Sacramento $5,000,000 |Chase Budinger, Minnesota $226,162 |Mustafa Shaku, Oklahoma City $11,046,000 |Richard Jefferson, Utah Butler Bucknell Brigham Young Boston College Blinn College|$1.4M Belmont |$0.5M Baylor |$7.1M Arkansas-LR |$0.8M Arkansas |$23.1M Arizona State|$16M Arizona |$54M Alabama |$16M 3 $510,000 |Carrick Felix, Cleveland $13,701,250 |James Hardin, Houston $1,750,000 |Jeff Ayres, San Antonio 3 21,466,718 |Joe Johnson 884,293 |Jannero Pargo, Charlotte 1 788,872 |Patrick Beverey, Houston 884,293 |Derek Fisher, Oklahoma City A completebreakdownofeveryNBAplayer’ssalary,wheretheyplayedbeforetheNBA,andwhichschoolscountriesproducehighestnetsalary. 4 4,469,548 |Ekpe Udoh, Milwaukee 788,872 |Quincy Acy, Sacramento 788,872 -

2010/11 Panini Limited Basketball Box Checklist
2010/11 Panini Limited Basketball Box Checklist Box Break Expectations: Case Break Expectations: 15 Boxes Per Case 3 Autograph or Memorabilia Cards Per Box ONE of following will be in each case: Guaranteed 1 Autograph 1 Limited Trios Autograph #/49 or less 1 Legend or Parallel Card #/199 or less 1 Autograph Prime Memorabilia #/10 3 Other Cards #/199 or less 1 Autograph Memorabilia Rookie RC Card 2010/11 Panini Limited Base Set Checklist Cards #/199 --- Find The Top Cards on eBay Below --- 1 Nate Robinson 21 Joakim Noah 41 Tyrus Thomas 61 Marc Gasol 81 Kevin Durant 2 Paul Pierce 22 Anderson Varejoao 42 Chris Bosh 62 OJ Mayo 82 Russell Westbrook 3 Rajon Rondo 23 Antawn Jamison 43 Dwyane Wade 63 Rudy Gay 83 Al Jefferson 4 Shaquille O'Neal 24 Mo Williams 44 LeBron James 64 Zach Randolph 84 Deron Williams 5 Brook Lopez 25 Ben Wallace 45 Mike Miller 65 Chris Paul 85 Raja Bell 6 Devin Harris 26 Richard Hamilton 46 Dwight Howard 66 Marcus Thornton 86 David Lee 7 Travis Outlaw 27 Rodney Stuckey 47 JJ REdick 67 Trevor Ariza 87 Monta Ellis 8 Amare Stoudemire 28 Tracy McGrady 48 Jason Williams 68 Manu Ginobili 88 Stephen Curry 9 Danilo Gallinari 29 Danny Granger 49 Rashard Lewis 69 Tim Duncan 89 Baron Davis 10 Raymond Felton 30 TJ Ford 50 JaVale McGee 70 Tony Parker 90 Blake Griffin 11 Toney Douglas 31 Tyler Hansbrough 51 Kirk Hinrich 71 Carmelo Anthony 91 Chris Kaman 12 Andre Iguodala 32 Andrew Bogut 52 Yi Jianlian 72 Chauncey Billups 92 Derek Fisher 13 Elton Brand 33 Brandon Jennings 53 Caron Butler 73 Chris Andersen 93 Kobe Bryant 14 Jrue Holiday -

June 30 Redemption Update
SET SUBSET/INSERT # PLAYER 2016 Panini Court Kings (16-17) Basketball Fresh Paint 39 Dario Saric Timothe Luwawu-Cabarrot 2016 Panini Court Kings (16-17) Basketball Fresh Paint Duals 10 Dario Saric 2016 Panini Court Kings (16-17) Basketball Fresh Paint Variation 39 Dario Saric 2016 Panini Gold Standard (16-17) Basketball Rookie Jersey Autographs 238 Dario Saric 2016 Panini Gold Standard (16-17) Basketball Rookie Jersey Autographs Double 269 Dario Saric 2016 Panini Gold Standard (16-17) Basketball Rookie Jersey Autographs Double Prime 269 Dario Saric 2016 Panini Gold Standard (16-17) Basketball Rookie Jersey Autographs Jumbos 338 Dario Saric 2016 Panini Gold Standard (16-17) Basketball Rookie Jersey Autographs Jumbos Prime 338 Dario Saric 2016 Panini Gold Standard (16-17) Basketball Rookie Jersey Autographs Jumbos Prime Tags 338 Dario Saric 2016 Panini Gold Standard (16-17) Basketball Rookie Jersey Autographs Prime 238 Dario Saric 2016 Panini Gold Standard (16-17) Basketball Rookie Jersey Autographs Triple 300 Dario Saric 2016 Panini Gold Standard (16-17) Basketball Rookie Jersey Autographs Triple Prime 300 Dario Saric 2016 Panini National Treasures (16-17) Basketball Colossal Jersey Autographs 29 Bojan Bogdanovic 2016 Panini National Treasures (16-17) Basketball Colossal Jersey Autographs Bronze 29 Bojan Bogdanovic 2016 Panini National Treasures (16-17) Basketball Hometown Heroes 42 Denzel Valentine 2016 Panini National Treasures (16-17) Basketball Hometown Heroes Bronze 42 Denzel Valentine 2016 Panini National Treasures (16-17) Basketball