What Is Statistics?
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Baseball Rule” Faces an Interesting Test
The “Baseball Rule” Faces an Interesting Test One of the many beauties of baseball, affectionately known as “America’s pastime,” is the ability for people to come to the stadium and become ingrained in the action and get the chance to interact with their heroes. Going to a baseball game, as opposed to going to most other sporting events, truly gives a fan the opportunity to take part in the action. However, this can come at a steep price as foul balls enter the stands at alarming speeds and occasionally strike spectators. According to a recent study, approximately 1,750 people get hurt each year by batted 1 balls at Major League Baseball (MLB) games, which adds up to twice every three games. The 2015 MLB season featured many serious incidents that shed light on the issue of 2 spectator protection. This has led to heated debates among the media, fans, and even players and 3 managers as to what should be done to combat this issue. Currently, there is a pending class action lawsuit against Major League Baseball (“MLB”). The lawsuit claims that MLB has not 1 David Glovin, Baseball Caught Looking as Fouls Injure 1,750 Fans a Year, BLOOMBERG BUSINESS (Sept. 9, 2014, 4:05 PM), http://www.bloomberg.com/news/articles/20140909/baseballcaughtlookingasfoulsinjure1750fansayear. 2 On June 5, a woman attending a Boston Red Sox game was struck in the head by a broken bat that flew into the seats along the third baseline. See Woman hurt by bat at Red Sox game released from hospital, NEW YORK POST (June 12, 2015, 9:32 PM), http://nypost.com/2015/06/12/womanhurtbybatatredsoxgamereleasedfromhospital/. -

BASE CARDS ARI-1 Zack Greinke Arizona Diamondbacks® ARI-2
BASE CARDS ARI-1 Zack Greinke Arizona Diamondbacks® ARI-2 Jake Lamb Arizona Diamondbacks® ARI-3 Ketel Marte Arizona Diamondbacks® ARI-4 Nick Ahmed Arizona Diamondbacks® ARI-5 Eduardo Escobar Arizona Diamondbacks® ARI-6 Robbie Ray Arizona Diamondbacks® ARI-7 Adam Jones Arizona Diamondbacks® ARI-8 Archie Bradley Arizona Diamondbacks® ARI-9 David Peralta Arizona Diamondbacks® ARI-10 Yoshihisa Hirano Arizona Diamondbacks® ATL-1 Ronald Acuña Jr. Atlanta Braves™ ATL-2 Freddie Freeman Atlanta Braves™ ATL-3 Ozzie Albies Atlanta Braves™ ATL-4 Dansby Swanson Atlanta Braves™ ATL-5 Ender Inciarte Atlanta Braves™ ATL-6 Mike Foltynewicz Atlanta Braves™ ATL-7 Johan Camargo Atlanta Braves™ ATL-8 Max Fried Atlanta Braves™ ATL-9 Josh Donaldson Atlanta Braves™ ATL-10 Hank Aaron Atlanta Braves™ BAL-1 Trey Mancini Baltimore Orioles® BAL-2 Oriole Bird Baltimore Orioles® BAL-3 Jonathan Villar Baltimore Orioles® BAL-4 Chris Davis Baltimore Orioles® BAL-5 Dylan Bundy Baltimore Orioles® BAL-6 Brandon Hyde Baltimore Orioles® BAL-7 Dwight Smith Jr. Baltimore Orioles® BAL-8 Richie Martin Baltimore Orioles® Rookie BAL-9 Richard Bleier Baltimore Orioles® BAL-10 Mychal Givens Baltimore Orioles® BOS-1 Mookie Betts Boston Red Sox® BOS-2 Chris Sale Boston Red Sox® BOS-3 David Price Boston Red Sox® BOS-4 Andrew Benintendi Boston Red Sox® BOS-5 J.D. Martinez Boston Red Sox® BOS-6 Dustin Pedroia Boston Red Sox® BOS-7 Xander Bogaerts Boston Red Sox® BOS-8 Rafael Devers Boston Red Sox® BOS-9 Steve Pearce Boston Red Sox® BOS-10 Jackie Bradley Jr. Boston Red Sox® CHC-1 Javier Báez Chicago Cubs® CHC-2 Anthony Rizzo Chicago Cubs® CHC-3 Kris Bryant Chicago Cubs® CHC-4 Jon Lester Chicago Cubs® CHC-5 Kyle Schwarber Chicago Cubs® CHC-6 Kyle Hendricks Chicago Cubs® CHC-7 Willson Contreras Chicago Cubs® CHC-8 David Bote Chicago Cubs® CHC-9 Albert Almora Jr. -

Download Preview
DETROIT TIGERS’ 4 GREATEST HITTERS Table of CONTENTS Contents Warm-Up, with a Side of Dedications ....................................................... 1 The Ty Cobb Birthplace Pilgrimage ......................................................... 9 1 Out of the Blocks—Into the Bleachers .............................................. 19 2 Quadruple Crown—Four’s Company, Five’s a Multitude ..................... 29 [Gates] Brown vs. Hot Dog .......................................................................................... 30 Prince Fielder Fields Macho Nacho ............................................................................. 30 Dangerfield Dangers .................................................................................................... 31 #1 Latino Hitters, Bar None ........................................................................................ 32 3 Hitting Prof Ted Williams, and the MACHO-METER ......................... 39 The MACHO-METER ..................................................................... 40 4 Miguel Cabrera, Knothole Kids, and the World’s Prettiest Girls ........... 47 Ty Cobb and the Presidential Passing Lane ................................................................. 49 The First Hammerin’ Hank—The Bronx’s Hank Greenberg ..................................... 50 Baseball and Heightism ............................................................................................... 53 One Amazing Baseball Record That Will Never Be Broken ...................................... -

SATURDAY, APRIL 23, 2016 at NEW YORK YANKEES LH Blake Snell (ML Debut) Vs
SATURDAY, APRIL 23, 2016 at NEW YORK YANKEES LH Blake Snell (ML Debut) vs. RH Mashiro Tanaka (1-0, 3.06) First Pitch: 1:05 p.m. | Location: Yankee Stadium, Bronx, N.Y. | TV: Fox Sports Sun | Radio: WDAE 620 AM, WGES 680 AM (Sp.) Game No.: 17 (7-9) | Road Game No.: 7 (2-4) | All-Time Game No.: 2,931 (1,359-1,571) | All-Time Road Game No.: 1,462 (610-851) RAY MATTER—The Rays opened this series with a 6-3 loss last night, the for-112) in the 8th or later and .210 (87-for-414) in innings 1-through-7… AL-high 12th time they have been to 3 runs or fewer (3-9)…the Rays are 4-0 the Rays have gone into the 7th inning stretch with a lead only three times. when they score more than 3 runs…22 pct. of the Rays runs this season came in one game, Thursday’s 12-8 win at Boston…Tampa Bay is 2-2 on vs. THE A.L. BEASTS—The Rays ($57M payroll) are on a 6-game road trip this 6-game trip (2-1 at Boston and 0-1 here)…Rays have won their last two to face the Red Sox ($191M payroll) and the Yankees ($222M payroll)…since series and are 4-2 in their last 6 games…they are 7-9 for the second time in 2010, the Rays are 61-53 vs. the Red Sox and 59-53 vs. the Yankees…their the past three years…they were 8-8 a year ago…this trip starts the Rays on a 120-106 record is the AL’s best combined record vs. -

Baseball Classics All-Time All-Star Greats Game Team Roster
BASEBALL CLASSICS® ALL-TIME ALL-STAR GREATS GAME TEAM ROSTER Baseball Classics has carefully analyzed and selected the top 400 Major League Baseball players voted to the All-Star team since it's inception in 1933. Incredibly, a total of 20 Cy Young or MVP winners were not voted to the All-Star team, but Baseball Classics included them in this amazing set for you to play. This rare collection of hand-selected superstars player cards are from the finest All-Star season to battle head-to-head across eras featuring 249 position players and 151 pitchers spanning 1933 to 2018! Enjoy endless hours of next generation MLB board game play managing these legendary ballplayers with color-coded player ratings based on years of time-tested algorithms to ensure they perform as they did in their careers. Enjoy Fast, Easy, & Statistically Accurate Baseball Classics next generation game play! Top 400 MLB All-Time All-Star Greats 1933 to present! Season/Team Player Season/Team Player Season/Team Player Season/Team Player 1933 Cincinnati Reds Chick Hafey 1942 St. Louis Cardinals Mort Cooper 1957 Milwaukee Braves Warren Spahn 1969 New York Mets Cleon Jones 1933 New York Giants Carl Hubbell 1942 St. Louis Cardinals Enos Slaughter 1957 Washington Senators Roy Sievers 1969 Oakland Athletics Reggie Jackson 1933 New York Yankees Babe Ruth 1943 New York Yankees Spud Chandler 1958 Boston Red Sox Jackie Jensen 1969 Pittsburgh Pirates Matty Alou 1933 New York Yankees Tony Lazzeri 1944 Boston Red Sox Bobby Doerr 1958 Chicago Cubs Ernie Banks 1969 San Francisco Giants Willie McCovey 1933 Philadelphia Athletics Jimmie Foxx 1944 St. -

2017 Information & Record Book
2017 INFORMATION & RECORD BOOK OWNERSHIP OF THE CLEVELAND INDIANS Paul J. Dolan John Sherman Owner/Chairman/Chief Executive Of¿ cer Vice Chairman The Dolan family's ownership of the Cleveland Indians enters its 18th season in 2017, while John Sherman was announced as Vice Chairman and minority ownership partner of the Paul Dolan begins his ¿ fth campaign as the primary control person of the franchise after Cleveland Indians on August 19, 2016. being formally approved by Major League Baseball on Jan. 10, 2013. Paul continues to A long-time entrepreneur and philanthropist, Sherman has been responsible for establishing serve as Chairman and Chief Executive Of¿ cer of the Indians, roles that he accepted prior two successful businesses in Kansas City, Missouri and has provided extensive charitable to the 2011 season. He began as Vice President, General Counsel of the Indians upon support throughout surrounding communities. joining the organization in 2000 and later served as the club's President from 2004-10. His ¿ rst startup, LPG Services Group, grew rapidly and merged with Dynegy (NYSE:DYN) Paul was born and raised in nearby Chardon, Ohio where he attended high school at in 1996. Sherman later founded Inergy L.P., which went public in 2001. He led Inergy Gilmour Academy in Gates Mills. He graduated with a B.A. degree from St. Lawrence through a period of tremendous growth, merging it with Crestwood Holdings in 2013, University in 1980 and received his Juris Doctorate from the University of Notre Dame’s and continues to serve on the board of [now] Crestwood Equity Partners (NYSE:CEQP). -
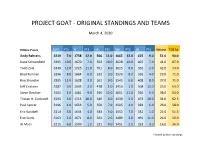
Project Goat - Original Standings and Teams
PROJECT GOAT - ORIGINAL STANDINGS AND TEAMS March 4, 2020 Hitting Points AVG PTS R PTS HR PTS RBI PTS SB PTS Hitting TOTAL Andy Behrens .3219 7.0 1738 12.0 566 11.0 1665 12.0 425 9.0 51.0 94.0 Dave Schoenfield .3295 10.0 1670 7.0 563 10.0 1628 10.0 407 7.0 44.0 87.0 Todd Zola .3339 12.0 1725 11.0 551 8.0 1615 9.0 352 2.0 42.0 73.0 Brad Kullman .3246 8.0 1664 6.0 512 3.0 1579 8.0 362 4.0 29.0 71.0 Ron Shandler .3305 11.0 1628 3.0 561 9.0 1545 6.0 408 8.0 37.0 71.0 Jeff Erickson .3287 9.0 1605 2.0 478 1.0 1410 1.0 508 12.0 25.0 63.0 Steve Gardner .3161 1.0 1681 9.0 596 12.0 1661 11.0 366 5.0 38.0 63.0 Tristan H. Cockcroft .3193 3.0 1713 10.0 546 6.0 1530 5.0 473 10.0 34.0 62.5 Paul Sporer .3196 4.0 1653 5.0 550 7.0 1505 4.0 392 6.0 26.0 58.0 Eric Karabell .3214 5.0 1644 4.0 543 5.0 1552 7.0 342 1.0 22.0 51.5 Eno Sarris .3163 2.0 1671 8.0 504 2.0 1489 3.0 491 11.0 26.0 50.0 AJ Mass .3215 6.0 1599 1.0 521 4.0 1451 2.0 353 3.0 16.0 36.0 *Sorted by final standings Pitching Points W PTS SV PTS K PTS ERA PTS WHIP PTS Pitching TOTAL Andy Behrens 187 11.5 0 1.5 2348 12.0 1.98 9.0 0.90 9.0 43.0 94.0 Dave Schoenfield 187 11.5 0 1.5 2288 11.0 1.95 11.0 0.91 8.0 43.0 87.0 Todd Zola 150 7.0 104 4.0 2154 8.0 2.03 7.0 0.95 5.0 31.0 73.0 Brad Kullman 141 4.5 141 10.5 1941 3.0 1.84 12.0 0.90 12.0 42.0 71.0 Ron Shandler 141 4.5 141 10.5 1886 2.0 1.97 10.0 0.93 7.0 34.0 71.0 Jeff Erickson 151 8.0 112 6.0 2130 6.0 2.01 8.0 0.90 10.0 38.0 63.0 Steve Gardner 147 6.0 105 5.0 2152 7.0 2.06 5.0 0.98 2.0 25.0 63.0 Tristan H. -

2021 Topps Dynamic Duals
Base Checklist 1 Ken Griffey Jr. Ronald Acuña Jr. 2 Kris Bryant Bryce Harper 3 Miguel Cabrera Casey Mize 4 John Smoltz Greg Maddux 5 Yadier Molina Buster Posey 6 Roger Clemens Pedro Martinez 7 Juan Soto Stephen Strasburg 8 Jose Abreu Frank Thomas 9 Corey Seager Cody Bellinger 10 Nolan Arenado Dylan Carlson 11 Trevor Bauer Shane Bieber 12 Matt Chapman Jose Canseco 13 Derek Jeter Mariano Rivera 14 Stan Musial Bob Gibson 15 Dwight Gooden Gary Carter 16 Alec Bohm Ke'Bryan Hayes 17 Xander Bogaerts Bobby Dalbec 18 Vladimir Guerrero Jr. Bo Bichette 19 Kyle Lewis Devin Williams 20 Freddie Freeman Cristian Pache 21 MIke Trout Jo Adell 22 Jacob deGrom Pete Alonso 23 Luis Garcia Nick Madrigal 24 Blake Snell Jake Cronenworth 25 Yordan Alvarez Randy Arozarena Autograph Checklist 1 Ken Griffey Jr. Ronald Acuña Jr. 2 Kris Bryant Bryce Harper 3 Miguel Cabrera Casey Mize 4 John Smoltz Greg Maddux 5 Yadier Molina Buster Posey 6 Roger Clemens Pedro Martinez 7 Juan Soto Stephen Strasburg 8 Jose Abreu Frank Thomas 9 Corey Seager Cody Bellinger 10 Nolan Arenado Dylan Carlson 11 Trevor Bauer Shane Bieber 12 Matt Chapman Jose Canseco 13 Derek Jeter Mariano Rivera 14 Stan Musial Bob Gibson 15 Dwight Gooden Gary Carter 16 Alec Bohm Ke'Bryan Hayes 17 Xander Bogaerts Bobby Dalbec 18 Vladimir Guerrero Jr. Bo Bichette 19 Kyle Lewis Devin Williams 20 Freddie Freeman Cristian Pache 21 MIke Trout Jo Adell 22 Jacob deGrom Pete Alonso 23 Luis Garcia Nick Madrigal 24 Blake Snell Jake Cronenworth 25 Yordan Alvarez Randy Arozarena Manager's Dream Insert MD-1 Mookie Betts Mike Trout MD-2 Fernando Tatis Jr. -

* Text Features
The Boston Red Sox Thursday, November 1, 2018 * The Boston Globe Why the Red Sox feel good about David Price going forward Alex Speier David Price came to Fenway Park ready to celebrate the Red Sox’ 2018 championship season, and hoping to do it again sometime in the next four years. Price had the right to opt out of the final four years and $127 million of the record-setting seven-year, $217 million deal he signed with the Red Sox after the 2015 season by midnight on Wednesday. However, as he basked in the afterglow of his first World Series title, the lefthander said that he would not leave the Red Sox. “I’m opting in. I’m not going anywhere. I want to win here. We did that this year and I want to do it again,” Price said minutes before boarding a duck boat. “There wasn’t any reconsideration on my part ever. I came here to win. We did that this year and that was very special, and now I want to do it again.” Red Sox principal owner (and Globe owner) John Henry was pleased with the decision. While industry opinion was nearly unanimous that Price wouldn’t have been able to make as much money on the open market as he will over the duration of his Red Sox deal, Henry said that the team wasn’t certain of the pitcher’s decision until he informed the club. “[Boston is] a tough town in many ways. I think [the opt-out] was there because it gave him an opportunity to see if he wanted to spend [all seven years here],” said Henry. -

A Summer Wildfire: How the Greatest Debut in Baseball History Peaked and Dwindled Over the Course of Three Months
The Report committee for Colin Thomas Reynolds Certifies that this is the approved version of the following report: A Summer Wildfire: How the greatest debut in baseball history peaked and dwindled over the course of three months APPROVED BY SUPERVISING COMMITTEE: Co-Supervisor: ______________________________________ Tracy Dahlby Co-Supervisor: ______________________________________ Bill Minutaglio ______________________________________ Dave Sheinin A Summer Wildfire: How the greatest debut in baseball history peaked and dwindled over the course of three months by Colin Thomas Reynolds, B.A. Report Presented to the Faculty of the Graduate School of the University of Texas at Austin in Partial Fulfillment of the Requirements for the Degree of Master of Arts The University of Texas at Austin May, 2011 To my parents, Lyn & Terry, without whom, none of this would be possible. Thank you. A Summer Wildfire: How the greatest debut in baseball history peaked and dwindled over the course of three months by Colin Thomas Reynolds, M.A. The University of Texas at Austin, 2011 SUPERVISORS: Tracy Dahlby & Bill Minutaglio The narrative itself is an ageless one, a fundamental Shakespearean tragedy in its progression. A young man is deemed invaluable and exalted by the public. The hero is cast into the spotlight and bestowed with insurmountable expectations. But the acclamations and pressures are burdensome and the invented savior fails to fulfill the prospects once imagined by the public. He is cast aside, disregarded as a symbol of failure or one deserving of pity. It’s the quintessential tragedy of a fallen hero. The protagonist of this report is Washington Nationals pitcher Stephen Strasburg, who enjoyed a phenomenal rookie season before it ended abruptly due to a severe elbow injury. -

Oregon State's Rutschman Named 2019 Dick Howser
DICK HOWSER TROPHY COMMITTEE Contact: Bo Carter ([email protected]) June 15, 2019 OREGON STATE’S RUTSCHMAN NAMED 2019 DICK HOWSER TROPHY RECIPIENT OMAHA, Neb. – Catcher Adley Rutschman of Oregon State is the 33rd recipient of the Dick Howser Trophy, presented by The Game Headwear, as college baseball's Player of the Year. The announcement came at a national news conference Saturday morning at TD Ameritrade Stadium as OSU’s first winner of the prestigious award met with a group of national media. He is the first Beavers player honored with the Howser Trophy, which originated in 1987. Rutschman also is the fourth recipient to be the first overall selection in the Major League Baseball free agent draft and capture the award, joining Clemson pitcher Kris Benson (1996), Vanderbilt pitcher David Price (2007) and San Diego State pitcher Steve Strasburg (2008). Rutchsman was selected by the Baltimore Orioles as the opening player in last week’s draft. The 2019 consensus first team All-America choice was honored in voting by the Howser Trophy committee and the National Collegiate Baseball Writers Association. He is the second all-time winner from the Pac-12 Conference after Mark Prior of Southern California captured the 2001 honor. Rutschman, a 6-2, 216-pound switch hitting and righty throwing junior catcher from Sherwood, Ore., also was the 2019 Pac-12 Player of the Year, the Pac-12 Defensive Player of the Year, and a finalist for the Buster Posey Award, which honors the nation’s top catcher in 2019 and is named in honor of the 2008 Dick Howser Trophy recipient. -

NABF Tournament News 09.Indd
November 1, 2009 • Bowie, Maryland • Price $1.00 95th Year Graduate of the Year NABF Graduates of the Year NABF Honors 1968 Bill Freehan (Detroit Tigers) 1969 Pete Rose (Cincinnati Reds) 1970 Bernie Carbo (Cincinnati Reds) 1971 Ted Simmons (St. Louis Cardinals) Zack Greinke 1972 John Mayberry (Kansas City The National Amateur Base- Royals) 1973 Sal Bando (Oakland Athletics) ball Federation is honoring Kan- 1974 Jim Wynn (Los Angeles Dodgers) sas City Royals pitcher Zack 1975 Frank Tanana (California Angels) Greinke is its 2009 Graduate of 1976 Rick Manning (Cleveland Indians) 1977 Kenton Tekulve (Pittsburgh the Year. Pirates) Greinke played on the NABF 1978 Lary Sorenson (Milwaukee 18 and under National Team in Brewers) 1979 Willie Horton (Seattle Mariners) 2001 in Joplin, Missouri — the 1980 Britt Burns (Chicago White Sox) fi rst year USA Baseball was in- 1981 Tom Paciorek (Seattle Mariners) 14 and under NABF Regional Classic Tournament action at Detwiler Park in Toledo, volved in the Tournament of 1982 Leon Durham (Chicago Cubs) Ohio (NABF photo by Harold Hamilton/www.hehphotos.lifepics.com). 1983 Robert Bonnell (Toronto Blue Stars. Jays) "He came to us 1984 Jack Perconte (Seattle Mariners) as a shortstop and 1985 John Franco (Cincinnati Reds) 2009 NABF Annual Meeting 1986 Jesse Barfi eld (Toronto Blue a possible pitcher," Jays) says NABF board 1987 Brian Fletcher (Texas Rangers) to be in Annapolis, Maryland member and na- 1988 Allen L. Anderson (Minnesota Twins) tional team busi- The 95th Annual Meeting of 1989 Dave Dravecky (San Fransisco ness manager Lou Tiberi. Giants) the National Amateur Baseball Greinke played shortstop and 1990 Barry Larkin (Cincinnati Reds) Federation will be Thursday, 1991 Steve Farr (New York Yankees) hit fourth during the fi rst four November 5 to Sunday, Novem- 1992 Marquies Grissom (Montreal games of the TOS.