Data Movement Optimization for High-Performance Computing
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

The Abcs of Petri Net Reachability Relaxations
The ABCs of Petri net reachability relaxations Michael Blondin, Universite´ de Sherbrooke, Canada Petri nets form a widespread model of concurrency well suited for the verification of systems with infinitely many configurations. Deciding configuration reachability in Petri nets, which plays a central role in their formal analysis, suffers from a nonelementary time complexity lower bound. We survey relaxations that alleviate this tremendous complexity, both for classical Petri nets and for extensions with affine transformations, branching rules and colored tokens. 1. INTRODUCTION Petri nets are a widespread formalism to model and analyze concurrent systems with possibly infinite configuration spaces over nonnegative counters, i.e. Nk. They offer a great tradeoff between graphical modeling and amenability to algorithmic analysis. In particular, they find applications ranging from program verification (e.g. [German and Sistla 1992; Kaiser et al. 2014; Atig et al. 2011; Delzanno et al. 2002]) to the for- mal analysis of chemical, biological and business processes (e.g. [Esparza et al. 2017; Heiner et al. 2008; van der Aalst 1998]). One of the central questions in Petri net the- ory consists in determining whether a given target configuration, typically an error of a system, is reachable from an initial configuration. This reachability problem, which we will shortly define formally, has been extensively studied over several decades. For a long time, the computational complexity of the problem lay between EXPSPACE- hardness [Lipton 1976] and decidability [Mayr 1981; Kosaraju 1982; Lambert 1992; Leroux 2012]. However, it was recently narrowed down between TOWER-hardness [Cz- erwinski´ et al. 2019], i.e. a tower of exponentials, and Ackermaniann time [Leroux and Schmitz 2019]. -

Adversarial Symbolic Execution for Detecting Concurrency-Related Cache Timing Leaks
Adversarial Symbolic Execution for Detecting Concurrency-Related Cache Timing Leaks Shengjian Guo Meng Wu Chao Wang Virginia Tech Virginia Tech University of Southern California Blacksburg, VA, USA Blacksburg, VA, USA Los Angeles, CA, USA ABSTRACT The timing characteristics of cache, a high-speed storage between Program P Adversarial the fast CPU and the slow memory, may reveal sensitive information (Thread T1) Thread Schedule of a program, thus allowing an adversary to conduct side-channel attacks. Existing methods for detecting timing leaks either ignore Concurrent Pro- Symbolic Cache-timing ′′ SMT Solving cache all together or focus only on passive leaks generated by the gram P Execution Leakage program itself, without considering leaks that are made possible by concurrently running some other threads. In this work, we show Program P′ Adversarial Cache that timing-leak-freedom is not a compositional property: a program (Thread T2) Cache Modeling Configuration that is not leaky when running alone may become leaky when inter- leaved with other threads. Thus, we develop a new method, named Figure 1: Flow of our cache timing leak detector SymSC. adversarial symbolic execution, to detect such leaks. It systematically explores both the feasible program paths and their interleavings while modeling the cache, and leverages an SMT solver to decide if are caused by differences in the number and type of instructions there are timing leaks. We have implemented our method in LLVM executed along different paths: unless the differences are indepen- and evaluated it on a set of real-world ciphers with 14,455 lines of dent of the sensitive data, they may be exploited by an adversary. -

1 Employment 2 Education 3 Grants
STEPHEN F. SIEGEL Curriculum Vitæ Department of Computer and Information Sciences email: [email protected] 101 Smith Hall web: http://vsl.cis.udel.edu/siegel.html University of Delaware tel: (302) 831{0083, fax: (302) 831{8458 Newark, DE 19716 skype: sfsiegel 1 Employment Associate Professor, Department of Computer and Information Sciences and Department of Math- ematical Sciences, University of Delaware, September 2012 to present Assistant Professor, Department of Computer and Information Sciences and Department of Math- ematical Sciences, University of Delaware, September 2006 to August 2012 Senior Research Scientist, Laboratory for Advanced Software Engineering Research, Department of Computer Science, University of Massachusetts Amherst, August 2001 to August 2006 Senior Software Engineer, Laboratory for Advanced Software Engineering Research, Department of Computer Science, University of Massachusetts Amherst, August 1998 to July 2001 Visiting Assistant Professor, Department of Mathematics, University of Massachusetts Amherst, September 1996 to August 1998 Visiting Assistant Professor, Department of Mathematics, Northwestern University, September 1993 to June 1996 2 Education Ph.D., Mathematics, University of Chicago, August 1993 (Advisor: Prof. Jonathan L. Alperin) M.Sc., Mathematics, Oxford University, June 1989 B.A., Mathematics, University of Chicago, June 1988 3 Grants Awarded • Principal Investigator, Subcontract 4000159498, Oak Ridge National Laboratory, Extend and Improve the CIVL Software Verification Platform. January 31, 2018 { September 30, 2020. Award amount: $245,963 (sole PI). Subcontract under Department of Energy award RAPIDS: A SciDAC Institute for Computer Science and Data. • Principal Investigator, Department of Energy Award DE-SC0012566, Program Verification for Extreme- Scale Applications, September 1, 2014 { August 31, 2018. Award amount: $510,000. (Sole PI) • Principal Investigator, National Science Foundation Award NSF CCF-1319571, SHF: Small: Con- tracts for Message-Passing Parallel Programs, September 1, 2013 { August 31, 2018. -

SIGLOG: Special Interest Group on Logic and Computation a Proposal
SIGLOG: Special Interest Group on Logic and Computation A Proposal Natarajan Shankar Computer Science Laboratory SRI International Menlo Park, CA Mar 21, 2014 SIGLOG: Executive Summary Logic is, and will continue to be, a central topic in computing. ACM has a core constituency with an interest in Logic and Computation (L&C), witnessed by 1 The many Turing Awards for work centrally in L&C 2 The ACM journal Transactions on Computational Logic 3 Several long-running conferences like LICS, CADE, CAV, ICLP, RTA, CSL, TACAS, and MFPS, and super-conferences like FLoC and ETAPS SIGLOG explores the connections between logic and computing covering theory, semantics, analysis, and synthesis. SIGLOG delivers value to its membership through the coordination of conferences, journals, newsletters, awards, and educational programs. SIGLOG enjoys significant synergies with several existing SIGs. Natarajan Shankar SIGLOG 2/9 Logic and Computation: Early Foundations Logicians like Alonzo Church, Kurt G¨odel, Alan Turing, John von Neumann, and Stephen Kleene have played a pioneering role in laying the foundation of computing. In the last 65 years, logic has become the calculus of computing underpinning the foundations of many diverse sub-fields. Natarajan Shankar SIGLOG 3/9 Logic and Computation: Turing Awardees Turing awardees for logic-related work include John McCarthy, Edsger Dijkstra, Dana Scott Michael Rabin, Tony Hoare Steve Cook, Robin Milner Amir Pnueli, Ed Clarke Allen Emerson Joseph Sifakis Leslie Lamport Natarajan Shankar SIGLOG 4/9 Interaction between SIGLOG and other SIGs Logic interacts in a significant way with AI (SIGAI), theory of computation (SIGACT), databases (SIGMOD) and knowledge bases (SIGKDD), programming languages (SIGPLAN), software engineering (SIGSOFT), computational biology (SIGBio), symbolic computing (SIGSAM), semantic web (SIGWEB), and hardware design (SIGDA and SIGARCH). -

Stephanie Weirich –
Stephanie Weirich School of Engineering and Science, University of Pennsylvania Levine 510, 3330 Walnut St, Philadelphia, PA 19104 215-573-2821 • [email protected] July 13, 2021 Positions University of Pennsylvania Philadelphia, Pennsylvania ENIAC President’s Distinguished Professor September 2019-present Galois, Inc Portland, Oregon Visiting Scientist June 2018-August 2019 University of Pennsylvania Philadelphia, Pennsylvania Professor July 2015-August 2019 University of Pennsylvania Philadelphia, Pennsylvania Associate Professor July 2008-June 2015 University of Cambridge Cambridge, UK Visitor August 2009-July 2010 Microsoft Research Cambridge, UK Visiting Researcher September-November 2009 University of Pennsylvania Philadelphia, Pennsylvania Assistant Professor July 2002-July 2008 Cornell University Ithaca, New York Instructor, Research Assistant and Teaching AssistantAugust 1996-July 2002 Lucent Technologies Murray Hill, New Jersey Intern June-July 1999 Education Cornell University Ithaca, NY Ph.D., Computer Science 2002 Cornell University Ithaca, NY M.S., Computer Science 2000 Rice University Houston, TX B.A., Computer Science, magnum cum laude 1996 Honors ○␣ SIGPLAN Robin Milner Young Researcher award, 2016 ○␣ Most Influential ICFP 2006 Paper, awarded in 2016 ○␣ Microsoft Outstanding Collaborator, 2016 ○␣ Penn Engineering Fellow, University of Pennsylvania, 2014 ○␣ Institute for Defense Analyses Computer Science Study Panel, 2007 ○␣ National Science Foundation CAREER Award, 2003 ○␣ Intel Graduate Student Fellowship, 2000–2001 -

Model Checking Randomized Distributed Algorithms Nathalie Bertrand
Model checking randomized distributed algorithms Nathalie Bertrand To cite this version: Nathalie Bertrand. Model checking randomized distributed algorithms. ACM SIGLOG News, ACM, 2020, 7 (1), pp.35-45. 10.1145/3385634.3385638. hal-03095637 HAL Id: hal-03095637 https://hal.inria.fr/hal-03095637 Submitted on 21 Jun 2021 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Model checking randomized distributed algorithms Nathalie Bertrand, Univ. Rennes, Inria, CNRS, IRISA – Rennes (France) Randomization is a powerful paradigm to solve hard problems, especially in distributed computing. Proving the correctness, and assessing the performances, of randomized distributed algorithms, is a very challenging research objective, that the verification community has started to address. In this article, we review existing model checking approaches to the verification of randomized distributed algorithms and identify further research directions. 1. RANDOMIZED DISTRIBUTED ALGORITHMS Distributed algorithms appear in a variety of applications and of frameworks. Emblematic applications include telecommunications, scientific computing, and Blockchain that received recently a lot of attention. Although one could think dis- tributed algorithms necessarily run on processors that are geographically distributed, the term also applies to algorithms running on shared-memory multiprocessors. -
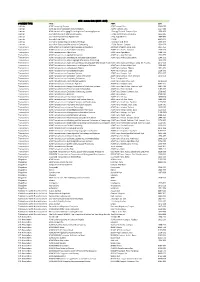
A ACM Transactions on Trans. 1553 TITLE ABBR ISSN ACM Computing Surveys ACM Comput. Surv. 0360‐0300 ACM Journal
ACM - zoznam titulov (2016 - 2019) CONTENT TYPE TITLE ABBR ISSN Journals ACM Computing Surveys ACM Comput. Surv. 0360‐0300 Journals ACM Journal of Computer Documentation ACM J. Comput. Doc. 1527‐6805 Journals ACM Journal on Emerging Technologies in Computing Systems J. Emerg. Technol. Comput. Syst. 1550‐4832 Journals Journal of Data and Information Quality J. Data and Information Quality 1936‐1955 Journals Journal of Experimental Algorithmics J. Exp. Algorithmics 1084‐6654 Journals Journal of the ACM J. ACM 0004‐5411 Journals Journal on Computing and Cultural Heritage J. Comput. Cult. Herit. 1556‐4673 Journals Journal on Educational Resources in Computing J. Educ. Resour. Comput. 1531‐4278 Transactions ACM Letters on Programming Languages and Systems ACM Lett. Program. Lang. Syst. 1057‐4514 Transactions ACM Transactions on Accessible Computing ACM Trans. Access. Comput. 1936‐7228 Transactions ACM Transactions on Algorithms ACM Trans. Algorithms 1549‐6325 Transactions ACM Transactions on Applied Perception ACM Trans. Appl. Percept. 1544‐3558 Transactions ACM Transactions on Architecture and Code Optimization ACM Trans. Archit. Code Optim. 1544‐3566 Transactions ACM Transactions on Asian Language Information Processing 1530‐0226 Transactions ACM Transactions on Asian and Low‐Resource Language Information Proce ACM Trans. Asian Low‐Resour. Lang. Inf. Process. 2375‐4699 Transactions ACM Transactions on Autonomous and Adaptive Systems ACM Trans. Auton. Adapt. Syst. 1556‐4665 Transactions ACM Transactions on Computation Theory ACM Trans. Comput. Theory 1942‐3454 Transactions ACM Transactions on Computational Logic ACM Trans. Comput. Logic 1529‐3785 Transactions ACM Transactions on Computer Systems ACM Trans. Comput. Syst. 0734‐2071 Transactions ACM Transactions on Computer‐Human Interaction ACM Trans. -
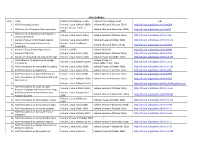
ACM JOURNALS S.No. TITLE PUBLICATION RANGE :STARTS PUBLICATION RANGE: LATEST URL 1. ACM Computing Surveys Volume 1 Issue 1
ACM JOURNALS S.No. TITLE PUBLICATION RANGE :STARTS PUBLICATION RANGE: LATEST URL 1. ACM Computing Surveys Volume 1 Issue 1 (March 1969) Volume 49 Issue 3 (October 2016) http://dl.acm.org/citation.cfm?id=J204 Volume 24 Issue 1 (Feb. 1, 2. ACM Journal of Computer Documentation Volume 26 Issue 4 (November 2002) http://dl.acm.org/citation.cfm?id=J24 2000) ACM Journal on Emerging Technologies in 3. Volume 1 Issue 1 (April 2005) Volume 13 Issue 2 (October 2016) http://dl.acm.org/citation.cfm?id=J967 Computing Systems 4. Journal of Data and Information Quality Volume 1 Issue 1 (June 2009) Volume 8 Issue 1 (October 2016) http://dl.acm.org/citation.cfm?id=J1191 Journal on Educational Resources in Volume 1 Issue 1es (March 5. Volume 16 Issue 2 (March 2016) http://dl.acm.org/citation.cfm?id=J814 Computing 2001) 6. Journal of Experimental Algorithmics Volume 1 (1996) Volume 21 (2016) http://dl.acm.org/citation.cfm?id=J430 7. Journal of the ACM Volume 1 Issue 1 (Jan. 1954) Volume 63 Issue 4 (October 2016) http://dl.acm.org/citation.cfm?id=J401 8. Journal on Computing and Cultural Heritage Volume 1 Issue 1 (June 2008) Volume 9 Issue 3 (October 2016) http://dl.acm.org/citation.cfm?id=J1157 ACM Letters on Programming Languages Volume 2 Issue 1-4 9. Volume 1 Issue 1 (March 1992) http://dl.acm.org/citation.cfm?id=J513 and Systems (March–Dec. 1993) 10. ACM Transactions on Accessible Computing Volume 1 Issue 1 (May 2008) Volume 9 Issue 1 (October 2016) http://dl.acm.org/citation.cfm?id=J1156 11. -

ACM SIGLOG News 1 October 2015, Vol
Volume 2, Number 4 Published by the Association for Computing Machinery Special Interest Group on Logic and Computation October 2015 SIGLOG news TABLE OF CONTENTS General Information 1 From the Editor Andrzej Murawski 2 Chair's Letter Prakash Panangaden Technical Columns 3 Automata Mikołaj Bojańczyk 16 Verication Neha Rungta Announcements 26 Gödel Prize - Call for Nominations 28 SIGLOG Monthly 175 SIGLOG NEWS Published by the ACM Special Interest Group on Logic and Computation SIGLOG Executive Committee Chair Prakash Panangaden McGill University Vice-Chair Luke Ong University of Oxford Treasurer Natarajan Shankar SRI International Secretary Alexandra Silva Radboud University Nijmegen Catuscia Palamidessi INRIA and LIX, Ecole´ Polytechnique EACSL President Anuj Dawar University of Cambridge EATCS President Luca Aceto Reykjavik University ACM ToCL E-in-C Dale Miller INRIA and LIX, Ecole´ Polytechnique Andrzej Murawski University of Warwick Veronique´ Cortier CNRS and LORIA, Nancy ADVISORY BOARD Mart´ın Abadi Google and UC Santa Cruz Phokion Kolaitis University of California, Santa Cruz Dexter Kozen Cornell University Gordon Plotkin University of Edinburgh Moshe Vardi Rice University COLUMN EDITORS Automata Mikołaj Bojanczyk´ University of Warsaw Complexity Neil Immerman University of Massachusetts Amherst Security and Privacy Matteo Maffei CISPA, Saarland University Semantics Mike Mislove Tulane University Verification Neha Rungta SGT Inc. and NASA Ames Notice to Contributing Authors to SIG Newsletters By submitting your article for distribution -

A Deep Dive Into the Weisfeiler-Leman Algorithm
A Deep Dive into the Weisfeiler-Leman Algorithm Martin Grohe # RWTH Aachen University, Germany Abstract The Weisfeiler-Leman algorithm is a well-known combinatorial graph isomorphism test going back to work of Weisfeiler and Leman in the late 1960s. The algorithm has a surprising number of seemingly unrelated characterisations in terms of logic, algebra, linear and semi-definite programming, and graph homomorphisms. Due to its simplicity and efficiency, it is an important subroutine of all modern graph isomorphism tools. In recent years, further applications in linear optimisation, probabilistic inference, and machine learning have surfaced. In my talk, I will introduce the Weisfeiler-Leman algorithm and some extensions. I will discuss its expressiveness and the various characterisations, and I will speak about its applications. 2012 ACM Subject Classification Mathematics of computing → Graph theory; Theory of computa- tion → Logic Keywords and phrases Weisfeiler-Leman algorithm, graph isomorphism, counting homomorphisms, finite variable logics Digital Object Identifier 10.4230/LIPIcs.MFCS.2021.2 Category Invited Talk References 1 Martin Grohe. word2vec, node2vec, graph2vec, x2vec: Towards a theory of vector embeddings of structured data. In Dan Suciu, Yufei Tao, and Zhewei Wei, editors, Proceedings of the 39th ACM SIGMOD-SIGACT-SIGART Symposium on Principles of Database Systems, pages 1–16, 2020. doi:10.1145/3375395.3387641. 2 Martin Grohe. The logic of graph neural networks. In Proceedings of the 36th ACM-IEEE Symposium on Logic in Computer Science, 2021. 3 Martin Grohe, Kristian Kersting, Martin Mladenov, and Pascal Schweitzer. Color re- finement and its applications. In G. Van den Broeck, K. Kersting, S. Natarajan, and D. -

Verifying Pufferfish Privacy in Hidden Markov Models
Verifying Pufferfish Privacy in Hidden Markov Models DEPENG LIU, Institute of Software, Chinese Academy of Sciences and University of Chinese Academy of Sciences BOW-YAW WANG, Institute of Information Science, Academia Sinica LIJUN ZHANG, Institute of Software, Chinese Academy of Sciences and University of Chinese Academy of Sciences Pufferfish is a Bayesian privacy framework for designing and analyzing privacy mechanisms. It refines differen- tial privacy, the current gold standard in data privacy, by allowing explicit prior knowledge in privacy analysis. Through these privacy frameworks, a number of privacy mechanisms have been developed in literature. In practice, privacy mechanisms often need be modified or adjusted to specific applications. Their privacy risks have to be re-evaluated for different circumstances. Moreover, computing devices only approximate continuous noises through floating-point computation, which is discrete in nature. Privacy proofs can thusbe complicated and prone to errors. Such tedious tasks can be burdensome to average data curators. In this paper, we propose an automatic verification technique for Pufferfish privacy. We use hidden Markov models tospecify and analyze discretized Pufferfish privacy mechanisms. We show that the Pufferfish verification problemin hidden Markov models is NP-hard. Using Satisfiability Modulo Theories solvers, we propose an algorithm to analyze privacy requirements. We implement our algorithm in a prototypical tool called FAIER, and present several case studies. Surprisingly, our case studies show that naïve discretization of well-established privacy mechanisms often fail, witnessed by counterexamples generated by FAIER. In discretized Above Threshold, we show that it results in absolutely no privacy. Finally, we compare our approach with testing based approach on several case studies, and show that our verification technique can be combined with testing based approach for the purpose of (i) efficiently certifying counterexamples and (ii) obtaining a better lower bound forthe privacy budget ϵ. -

Candidate for Chair Frank Pfenning Carnegie Mellon University
Candidate for Chair Frank Pfenning Carnegie Mellon University, Pittsburgh, PA, USA BIOGRAPHY Academic Background: Ph.D., Carnegie Mellon University, 1987, Mathematics. Professional Experience: Professor, Computer Science Department, Carnegie Mellon University, Pittsburgh, PA, USA, 2002 – Present; Head, Computer Science Department, Carnegie Mellon University, Pittsburgh, PA, USA, 2013 – 2018; Associate Dean, School of Computer Science, Carnegie Mellon University, Pittsburgh, PA, USA, 2009 – 2010. Professional Interest: Type theory; Automated deduction; Logical frameworks; Computer security; Computer science education. ACM Activities: Member of LICS Steering Committee, SIGLOG, 2008-2010 & 2018 – Present; Program Chair, LICS 2008, ACM/IEEE (now: SIGLOG/IEEE); General Chair, PPDP 2002, ACM SIGPLAN; Program Chair, PPDP 2000, ACM SIGPLAN. Membership and Offices in Related Organizations: Member of FoSSaCS Steering Committee, ETAPS, 2018 – Present; President, CADE, 2008 – 2009; Trustee, CADE, 1998 – 2004. Awards Received: LICS Test-of-Time Award (with I. Cervesato) for LICS'96 paper, 2016; ACM Fellow, 2015; Alexander-von-Humboldt Fellowship, 1996; Fulbright Fellowship, 1980. STATEMENT I have always considered ‘Logic in Computer Science’ my primary area of research, pervading my work on logical frameworks, type theory, automated deduction, logic programming, computer security, and computer science education. I am therefore pleased to offer my services to SIGLOG as a way to give back to the community that has been instrumental to my academic career (including 11 papers published at LICS, 4 in ToCL, and serving on the LICS PC 8 times). Already, SIGLOG has made a significant difference through sponsorship of conferences, publications, and awards, and there are opportunities for growth in these activities. For example, additional awards such as a dissertation award and a service award would recognize leadership efforts and benefit young researchers.