On the Size, Shape, and Density of Dwarf Planet Makemake
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Dwarf Planet Ceres
Dwarf Planet Ceres drishtiias.com/printpdf/dwarf-planet-ceres Why in News As per the data collected by NASA’s Dawn spacecraft, dwarf planet Ceres reportedly has salty water underground. Dawn (2007-18) was a mission to the two most massive bodies in the main asteroid belt - Vesta and Ceres. Key Points 1/3 Latest Findings: The scientists have given Ceres the status of an “ocean world” as it has a big reservoir of salty water underneath its frigid surface. This has led to an increased interest of scientists that the dwarf planet was maybe habitable or has the potential to be. Ocean Worlds is a term for ‘Water in the Solar System and Beyond’. The salty water originated in a brine reservoir spread hundreds of miles and about 40 km beneath the surface of the Ceres. Further, there is an evidence that Ceres remains geologically active with cryovolcanism - volcanoes oozing icy material. Instead of molten rock, cryovolcanoes or salty-mud volcanoes release frigid, salty water sometimes mixed with mud. Subsurface Oceans on other Celestial Bodies: Jupiter’s moon Europa, Saturn’s moon Enceladus, Neptune’s moon Triton, and the dwarf planet Pluto. This provides scientists a means to understand the history of the solar system. Ceres: It is the largest object in the asteroid belt between Mars and Jupiter. It was the first member of the asteroid belt to be discovered when Giuseppe Piazzi spotted it in 1801. It is the only dwarf planet located in the inner solar system (includes planets Mercury, Venus, Earth and Mars). Scientists classified it as a dwarf planet in 2006. -

Mass of the Kuiper Belt · 9Th Planet PACS 95.10.Ce · 96.12.De · 96.12.Fe · 96.20.-N · 96.30.-T
Celestial Mechanics and Dynamical Astronomy manuscript No. (will be inserted by the editor) Mass of the Kuiper Belt E. V. Pitjeva · N. P. Pitjev Received: 13 December 2017 / Accepted: 24 August 2018 The final publication ia available at Springer via http://doi.org/10.1007/s10569-018-9853-5 Abstract The Kuiper belt includes tens of thousands of large bodies and millions of smaller objects. The main part of the belt objects is located in the annular zone between 39.4 au and 47.8 au from the Sun, the boundaries correspond to the average distances for orbital resonances 3:2 and 2:1 with the motion of Neptune. One-dimensional, two-dimensional, and discrete rings to model the total gravitational attraction of numerous belt objects are consid- ered. The discrete rotating model most correctly reflects the real interaction of bodies in the Solar system. The masses of the model rings were determined within EPM2017—the new version of ephemerides of planets and the Moon at IAA RAS—by fitting spacecraft ranging observations. The total mass of the Kuiper belt was calculated as the sum of the masses of the 31 largest trans-neptunian objects directly included in the simultaneous integration and the estimated mass of the model of the discrete ring of TNO. The total mass −2 is (1.97 ± 0.30) · 10 m⊕. The gravitational influence of the Kuiper belt on Jupiter, Saturn, Uranus and Neptune exceeds at times the attraction of the hypothetical 9th planet with a mass of ∼ 10 m⊕ at the distances assumed for it. -
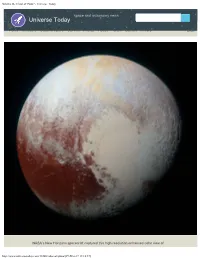
What Is the Color of Pluto? - Universe Today
What is the Color of Pluto? - Universe Today space and astronomy news Universe Today Home Members Guide to Space Carnival Photos Videos Forum Contact Privacy Login NASA’s New Horizons spacecraft captured this high-resolution enhanced color view of http://www.universetoday.com/13866/color-of-pluto/[29-Mar-17 13:18:37] What is the Color of Pluto? - Universe Today Pluto on July 14, 2015. Credit: NASA/JHUAPL/SwRI WHAT IS THE COLOR OF PLUTO? Article Updated: 28 Mar , 2017 by Matt Williams When Pluto was first discovered by Clybe Tombaugh in 1930, astronomers believed that they had found the ninth and outermost planet of the Solar System. In the decades that followed, what little we were able to learn about this distant world was the product of surveys conducted using Earth-based telescopes. Throughout this period, astronomers believed that Pluto was a dirty brown color. In recent years, thanks to improved observations and the New Horizons mission, we have finally managed to obtain a clear picture of what Pluto looks like. In addition to information about its surface features, composition and tenuous atmosphere, much has been learned about Pluto’s appearance. Because of this, we now know that the one-time “ninth planet” of the Solar System is rich and varied in color. Composition: With a mean density of 1.87 g/cm3, Pluto’s composition is differentiated between an icy mantle and a rocky core. The surface is composed of more than 98% nitrogen ice, with traces of methane and carbon monoxide. Scientists also suspect that Pluto’s internal structure is differentiated, with the rocky material having settled into a dense core surrounded by a mantle of water ice. -

The Solar System Cause Impact Craters
ASTRONOMY 161 Introduction to Solar System Astronomy Class 12 Solar System Survey Monday, February 5 Key Concepts (1) The terrestrial planets are made primarily of rock and metal. (2) The Jovian planets are made primarily of hydrogen and helium. (3) Moons (a.k.a. satellites) orbit the planets; some moons are large. (4) Asteroids, meteoroids, comets, and Kuiper Belt objects orbit the Sun. (5) Collision between objects in the Solar System cause impact craters. Family portrait of the Solar System: Mercury, Venus, Earth, Mars, Jupiter, Saturn, Uranus, Neptune, (Eris, Ceres, Pluto): My Very Excellent Mother Just Served Us Nine (Extra Cheese Pizzas). The Solar System: List of Ingredients Ingredient Percent of total mass Sun 99.8% Jupiter 0.1% other planets 0.05% everything else 0.05% The Sun dominates the Solar System Jupiter dominates the planets Object Mass Object Mass 1) Sun 330,000 2) Jupiter 320 10) Ganymede 0.025 3) Saturn 95 11) Titan 0.023 4) Neptune 17 12) Callisto 0.018 5) Uranus 15 13) Io 0.015 6) Earth 1.0 14) Moon 0.012 7) Venus 0.82 15) Europa 0.008 8) Mars 0.11 16) Triton 0.004 9) Mercury 0.055 17) Pluto 0.002 A few words about the Sun. The Sun is a large sphere of gas (mostly H, He – hydrogen and helium). The Sun shines because it is hot (T = 5,800 K). The Sun remains hot because it is powered by fusion of hydrogen to helium (H-bomb). (1) The terrestrial planets are made primarily of rock and metal. -

International Astronomical Union Union Astronomique Internationale
INTERNATIONAL ASTRONOMICAL UNION UNION ASTRONOMIQUE INTERNATIONALE ************ IAU0806: FOR IMMEDIATE RELEASE ************ http://www.iau.org/public_press/news/release/iau0806/ Fourth dwarf planet named Makemake 17 July 2008, Paris: The International Astronomical Union (IAU) has given the name Makemake to the newest member of the family of dwarf planets — the object formerly known as 2005 FY9 —after the Polynesian creator of humanity and the god of fertility. Members of the International Astronomical Union’s Committee on Small Body Nomenclature (CSBN) and the IAU Working Group for Planetary System Nomenclature (WGPSN) have decided to name the newest member of the plutoid family Makemake, and have classified it as the fourth dwarf planet in our Solar System and the third plutoid. Makemake (pronounced MAH-keh MAH-keh) is one of the largest objects known in the outer Solar System and is just slightly smaller and dimmer than Pluto, its fellow plutoid. The dwarf planet is reddish in colour and astronomers believe the surface is covered by a layer of frozen methane. Like other plutoids, Makemake is located in a region beyond Neptune that is populated with small Solar System bodies (often referred to as the transneptunian region). The object was discovered in 2005 by a team from the California Institute of Technology led by Mike Brown and was previously known as 2005 FY9 (or unofficially “Easterbunny”). It has the IAU Minor Planet Center designation (136472). Once the orbit of a small Solar System body or candidate dwarf planet is well determined, its provisional designation (2005 FY9 in the case of Makemake) is superseded by its permanent numerical designation (136472) in the case of Makemake. -

Distant Ekos
Issue No. 51 March 2007 s DISTANT EKO di The Kuiper Belt Electronic Newsletter r Edited by: Joel Wm. Parker [email protected] www.boulder.swri.edu/ekonews CONTENTS News & Announcements ................................. 2 Abstracts of 6 Accepted Papers ......................... 3 Titles of 2 Submitted Papers ........................... 6 Title of 1 Other Paper of Interest ....................... 7 Title of 1 Conference Contribution ..................... 7 Abstracts of 3 Book Chapters ........................... 8 Newsletter Information .............................. 10 1 NEWS & ANNOUNCEMENTS More binaries...lots more... In IAUC 8811, 8814, 8815, and 8816, Noll et al. report satellites of five TNOs from HST observations: • (123509) 2000 WK183, separation = 0.080 arcsec, magnitude difference = 0.4 mag • 2002 WC19, separation = 0.090 arcsec, magnitude difference = 2.5 mag • 2002 GZ31, separation = 0.070 arcsec, magnitude difference = 1.0 mag • 2004 PB108, separation = 0.172 arcsec, magnitude difference = 1.2 mag • (60621) 2000 FE8, separation = 0.044 arcsec, magnitude difference = 0.6 mag In IAUC 8812, Brown and Suer report satellites of four TNOs from HST observations: • (50000) Quaoar, separation = 0.35 arcsec, magnitude difference = 5.6 mag • (55637) 2002 UX25, separation = 0.164 arcsec, magnitude difference = 2.5 mag • (90482) Orcus, separation = 0.25 arcsec, magnitude difference = 2.7 mag • 2003 AZ84, separation = 0.22 arcsec, magnitude difference = 5.0 mag ................................................... ................................................ -

Solar System Planet and Dwarf Planet Fact Sheet
Solar System Planet and Dwarf Planet Fact Sheet The planets and dwarf planets are listed in their order from the Sun. Mercury The smallest planet in the Solar System. The closest planet to the Sun. Revolves the fastest around the Sun. It is 1,000 degrees Fahrenheit hotter on its daytime side than on its night time side. Venus The hottest planet. Average temperature: 864 F. Hotter than your oven at home. It is covered in clouds of sulfuric acid. It rains sulfuric acid on Venus which comes down as virga and does not reach the surface of the planet. Its atmosphere is mostly carbon dioxide (CO2). It has thousands of volcanoes. Most are dormant. But some might be active. Scientists are not sure. It rotates around its axis slower than it revolves around the Sun. That means that its day is longer than its year! This rotation is the slowest in the Solar System. Earth Lots of water! Mountains! Active volcanoes! Hurricanes! Earthquakes! Life! Us! Mars It is sometimes called the "red planet" because it is covered in iron oxide -- a substance that is the same as rust on our planet. It has the highest volcano -- Olympus Mons -- in the Solar System. It is not an active volcano. It has a canyon -- Valles Marineris -- that is as wide as the United States. It once had rivers, lakes and oceans of water. Scientists are trying to find out what happened to all this water and if there ever was (or still is!) life on Mars. It sometimes has dust storms that cover the entire planet. -

Taxonomy of Trans-Neptunian Objects and Centaurs As Seen from Spectroscopy? F
A&A 604, A86 (2017) Astronomy DOI: 10.1051/0004-6361/201730933 & c ESO 2017 Astrophysics Taxonomy of trans-Neptunian objects and Centaurs as seen from spectroscopy? F. Merlin1, T. Hromakina2, D. Perna1, M. J. Hong1, and A. Alvarez-Candal3 1 LESIA – Observatoire de Paris, PSL Research University, CNRS, Sorbonne Universités, UPMC Univ. Paris 06, Univ. Paris Diderot, Sorbonne Paris Cité, 5 place Jules Janssen, 92195 Meudon, France e-mail: [email protected] 2 Institute of Astronomy, Kharkiv V. N. Karin National University, Sumska Str. 35, 61022 Kharkiv, Ukraine 3 Observatorio Nacional, R. Gal. Jose Cristino 77, 20921-400 Rio de Janeiro, Brazil Received 4 April 2017 / Accepted 19 May 2017 ABSTRACT Context. Taxonomy of trans-Neptunian objects (TNOs) and Centaurs has been made in previous works using broadband filters in the visible and near infrared ranges. This initial investigation led to the establishment of four groups with the aim to provide the mean colors of the different classes with possible links with any physical or chemical properties. However, this taxonomy was only made with the Johnson-Cousins filter system and the ESO J, H, Ks filters combination, and any association with other filter system is not yet available. Aims. We aim to edit complete visible to near infrared taxonomy and extend this work to any possible filters system. To do this, we generate mean spectra for each individual group, from a data set of 43 spectra. This work also presents new spectra of the TNO (38628) Huya, on which aqueous alteration has been suspected, and the Centaur 2007 VH305. -

The Kuiper Belt: What We Know and What We Don’T
The Kuiper Belt: What We Know and What We Don’t David Jewitt, UCLA, September 2012 The best indication of the significance of the Kuiper belt lies in its multiple connections to other aspects of the Solar system. The dust in the Zodiacal cloud, the rocks in the meteor streams, the nuclei of comets, the Centaurs, perhaps also the irregular moons of the planets and the Trojans that lead and trail planets in their orbits, are all related to the parent population in the Kuiper belt. Further afield, the dusty debris disks of other stars are likely produced by collisional shattering of parent bodies in unseen Kuiper belts about them. Because of these many connections, Kuiper belt science has already had significant impact on the study of the contents, origin and evolution of the Solar system, and on understanding the Solar system in the context set by other stars. While we know much more than we used to, we still don’t know many things about the Kuiper belt. The Solar system formed from a flattened, rotating disk of gas and dust, itself produced by gravitational collapse from the interstellar medium. The explosion of a nearby massive star, a “supernova”, may have provided the initial compression causing the cloud to collapse, as suggested by the products of decay of short-lived radioactive elements (esp. 26Al) embedded in meteorites (Lee et al. 1977, Dauphas and Chaussidon 2011). Planets formed quickly in the dense inner portions of this disk but the process of growth in the rarefied outer regions was very slow. -

Atmospheres and Surfaces of Small Bodies and Dwarf Planets in the Kuiper Belt
EPJ Web of Conferences 9, 267–276 (2010) DOI: 10.1051/epjconf/201009021 c Owned by the authors, published by EDP Sciences, 2010 Atmospheres and surfaces of small bodies and dwarf planets in the Kuiper Belt E.L. Schallera Lunar and Planetary Laboratory, University of Arizona, Tucson, AZ 85721, USA Abstract. Kuiper Belt Objects (KBOs) are icy relics orbiting the sun beyond Neptune left over from the planetary accretion disk. These bodies act as unique tracers of the chemical, thermal, and dynamical history of our solar system. Over 1000 Kuiper Belt Objects (KBOs) and centaurs (objects with perihelia between the giant planets) have been discovered over the past two decades. While the vast majority of these objects are small (< 500 km in diameter), there are now many objects known that are massive enough to attain hydrostatic equilibrium (and are therefore considered dwarf planets) including Pluto, Eris, MakeMake, and Haumea. The discoveries of these large objects, along with the advent of large (> 6-meter) telescopes, have allowed for the first detailed studies of their surfaces and atmospheres. Visible and near-infrared spectroscopy of KBOs and centaurs has revealed a great diversity of surface compositions. Only the largest and coldest objects are capable of retaining volatile ices and atmospheres. Knowledge of the dynamics, physical properties, and collisional history of objects in the Kuiper belt is important for understanding solar system formation and evolution. 1 Introduction The existence of a belt of debris beyond Neptune left over from planetary accretion was proposed by Kuiper in 1951 [1]. Though Pluto was discovered in 1930, it took over sixty years for other Kuiper belt objects (KBOs) to be detected [2] and for Pluto to be recognized as the first known member of a larger population now known to consist of over 1000 objects (Fig. -

Ice Ontnos: Focus on 136108 Haumea
Ice onTNOs: Focus on 136108 Haumea C. Dumas Collaborators: A. Alvarez, A. Barucci, C. deBergh, B. Carry, A. Guilbert, D. Hestroffer, P. Lacerda, F. deMeo, F. Merlin, C. Snodgrass, P. Vernazza, … Haumea Pluto (dwarf planets) DistribuTon of TNOs Largest TNOs Icy bodies in the OPSII context • Reservoir of volales in the solar system (H2O, N2, CH4, CO, CO2, C2H6, NH3OH, etc) • Small bodies populaon more hydrated than originally pictured – Main-belt comets (Hsieh and JewiZ 2006) – Themis asteroids family (Campins et al. 2010, Rivkin and Emery 2010) • Transport of water to the inner terrestrial planets (e.g. talk by Paul Hartogh) Paranal Observatory 6 SINFONI at UT4 7 SINFONI + NACO at UT4 8 SINFONI = MACAO + SPIFFI (SINFONI=Spectrograph for INtegral Field Observations in the Near Infrared) • AO SYSTEM: MACAO (Multi-Application Curvature Adaptive Optics): – Similar to UTs AO system for VLTI – 60 elements curvature sensing bimorph mirror – NGS or LGS – Developed by ESO • NEAR-IR SPECTRO: SPIFFI (SPectrometer for Infrared Faint Field Imaging): – 3-D spectrograph, 32 image slices, 1-2.5µm – Developed by MPE:Max Planck Institute for Extraterrestrial Physics + NOVA: Netherlands Research School for Astronomy SINFONI - Main characteristics • Location UT4 Cassegrain • Wavelength range 1-2.5µm • Detector 2048 x 2048 HAWAII array • Gratings J,H,K,H+K • Spectral resolution 1500 (H+K-filter) to 4000 (K-band) (outside OH lines) • Limiting magnitude (0.1”/spaxel) K~18.2, H+K~19.2 in hr, SNR~10 • FoV sampling 32 slices • Spatial resolution 0.25”/slice (no-AO), 0.1”(AO), 0.025” (AO) • Resulting FoV 8”x8”, 3”x3”, 0.8”x0.8” • Modes noAO, NGS-AO, LGS-AO SINFONI - IFS Principles SINFONI - IFS Principles (Cont’d) SINFONI - products Reconstructed image PSF spectrum H+K TNOs spectroscopy Orcus (Carry et al. -
Pluto and Its Cohorts, Which Is Not Ger Passing by and Falling in Love So Much When Compared to the with Her
INTERNATIONAL SPACE SCIENCE INSTITUTE SPATIUM Published by the Association Pro ISSI No. 33, March 2014 141348_Spatium_33_(001_016).indd 1 19.03.14 13:47 Editorial A sunny spring day. A green On 20 March 2013, Dr. Hermann meadow on the gentle slopes of Boehnhardt reported on the pre- Impressum Mount Etna and a handsome sent state of our knowledge of woman gathering flowers. A stran- Pluto and its cohorts, which is not ger passing by and falling in love so much when compared to the with her. planets in our cosmic neighbour- hood, yet impressively much in SPATIUM Next time, when she is picking view of their modest size and their Published by the flowers again, the foreigner returns gargantuan distance. In fact, ob- Association Pro ISSI on four black horses. Now, he, serving dwarf planet Pluto poses Pluto, the Roman god of the un- similar challenges to watching an derworld, carries off Proserpina to astronaut’s face on the Moon. marry her and live together in the shadowland. The heartbroken We thank Dr. Boehnhardt for his Association Pro ISSI mother Ceres insists on her return; kind permission to publishing Hallerstrasse 6, CH-3012 Bern she compromises with Pluto allow- herewith a summary of his fasci- Phone +41 (0)31 631 48 96 ing Proserpina to living under the nating talk for our Pro ISSI see light of the Sun during six months association. www.issibern.ch/pro-issi.html of a year, called summer from now for the whole Spatium series on, when the flowers bloom on the Hansjörg Schlaepfer slopes of Mount Etna, while hav- Brissago, March 2014 President ing to stay in the twilight of the Prof.