Scheme of Instruction 2019-20
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Scheme of Instruction 2018-19
Scheme of Instruction 2018-19 Contents A. Scheme of Instruction Course Page No. Prefix Preface 3 I Division of Biological Sciences Preface 6 Integrated Ph D Programme in Biological Sciences DB 7 Biochemistry BC 10 Ecological Sciences EC 13 Molecular Biophysics MB 15 Microbiology and Cell Biology MC 20 Molecular Reproduction, Development and Genetics RD 24 Neuroscience NS 26 II Division of Chemical Sciences Preface 28 Integrated Ph D Programme in Chemical Sciences CD 29 Inorganic and Physical Chemistry IP 34 Materials Research MR 38 Organic Chemistry OC 41 Solid State and Structural Chemistry SS 44 III Division of Physical and Mathematical Sciences Preface 47 Instrumentation and Applied Physics IN 48 Mathematics MA 55 Astronomy and Astrophysics AA 69 Physics and Integrated Ph D in Physical Sciences PH 70 High Energy Physics HE 84 IV Division of Electrical Sciences Preface 89 Core requirements for M Tech Degree Programmes M Tech Degree - Computer Science and Engineering M Tech Degree - Telecommunications M Tech Degree – Signal Processing M Tech Degree – Microelectronics Systems M Tech Degree – Electrical Engineering M Tech Degree – Systems Science and Automation M Tech Degree – Electronics Systems Engineering Computer Science and Automation Intelligent Systems and Automation Communication Systems 1 Electronic Devices, Circuits and Technology Power Energy Systems High Voltage and Insulation Systems Electronics and Power Drives Photonic Device Electromagnetics, Microwaves and Antennas Signal Processing, Acoustics and Bioengineering Dissertation -

CDRI Awards 2021 for Excellence in Drug Research
CDRI AWARDS for Excellence in Drug Research 2021 Invitation for Nominations / Applications Instituted by the CSIR-Central Drug Research Institute, Lucknow – 226 031 CDRI AWARDS for Excellence in Drug Research Preamble The CSIR-Central Drug Research Institute (CDRI), Lucknow, was seventh in the chain of CSIR labs that were established in India right after independence India with an aim for technological independence of the Nation. CSIR-CDRI was broadly mandated with the task to revolutionise the pharmaceutical sector, which was almost non-existent at that time for accessibility and affordability of drugs. Today, CSIR-CDRI has evolved into a unique institution possessing end-to-end expertise in the domain of new drug development –its human resource and infrastructure today is second to none. Besides being the breeding ground of huge highly trained human resource for the drug development and manufacturing, out of 20 new drugs discovered, developed and approved in the post-independent India, 11 (8 synthetic + 3 phytopharmaceuticals) are contributions of CSIR-CDRI, Lucknow. These include Centchroman, Arteether, Centbucridine, Gugulipid, Bacosides Enriched Standardized Extract of Bacopa, etc. Centchroman (Ormeloxifene), a non-steroidal contraceptive with almost no toxicity, is now part of the National Family Program, whereas α-β Arteether (antimalarial) is included in the National Malaria Program. However, from the National front, new drug discovery and development is still in its infancy in India. India is a leader in global generic pharmaceuticals manufacturing and is being called as Pharmacy of the developing world, however, many generics manufactured in India are at the end of their respective product life cycles. -

Annual Report 2013-2014
ANNUAL REPORT 2013 – 14 One Hundred and Fifth Year Indian Institute of Science Bangalore - 560 012 i ii Contents Page No Page No Preface 5.3 Departmental Seminars and IISc at a glance Colloquia 120 5.4 Visitors 120 1. The Institute 1-3 5.5 Faculty: Other Professional 1.1 Court 1 Services 121 1.2 Council 2 5.6 Outreach 121 1.3 Finance Committee 3 5.7 International Relations Cell 121 1.4 Senate 3 1.5 Faculties 3 6. Continuing Education 123-124 2. Staff 4-18 7. Sponsored Research, Scientific & 2.1 Listing 4 Industrial Consultancy 125-164 2.2 Changes 12 7.1 Centre for Sponsored Schemes 2.3 Awards/Distinctions 12 & Projects 125 7.2 Centre for Scientific & Industrial 3. Students 19-25 Consultancy 155 3.1 Admissions & On Roll 19 7.3 Intellectual Property Cell 162 3.2 SC/ST Students 19 7.4 Society for Innovation & 3.3 Scholarships/Fellowships 19 Development 163 3.4 Assistance Programme 19 7.5 Advanced Bio-residue Energy 3.5 Students Council 19 Technologies Society 164 3.6 Hostels 19 3.7 Award of Medals 19 8. Central Facilities 165-168 3.8 Placement 21 8.1 Infrastructure - Buildings 165 8.2 Activities 166 4. Research and Teaching 26-116 8.2.1 Official Language Unit 166 4.1 Research Highlights 26 8.2.2 SC/ST Cell 166 4.1.1 Biological Sciences 26 8.2.3 Counselling and Support Centre 167 4.1.2 Chemical Sciences 35 8.3 Women’s Cell 167 4.1.3 Electrical Sciences 46 8.4 Public Information Office 167 4.1.4 Mechanical Sciences 57 8.5 Alumni Association 167 4.1.5 Physical & Mathematical Sciences 75 8.6 Professional Societies 168 4.1.6 Centres under Director 91 4.2. -

Annual Report 2017-2018
ANNUAL REPORT IISc 2017-18 INDIAN INSTITUTE OF SCIENCE VISITOR The President of India PRESIDENT OF THE COURT N Chandrasekaran CHAIRMAN OF THE COUNCIL P Rama Rao DIRECTOR Anurag Kumar DEANS SCIENCE: Biman Bagchi ENGINEERING: K Kesava Rao UG PROGRAMME: Anjali A Karande REGISTRAR V Rajarajan Pg 3 IISc RANKED INDIA’S TOP UNIVERSITY In 2016, IISc was ranked Number 1 among universities by the National Institutional Ranking Framework (NIRF) under the auspices of the Ministry of Human Resource Development. It was the first time the NIRF came out with rankings for Indian universities and institutions of higher education. In both 2017 and 2018, the Institute was again ranked first among universities, as well as first in the overall category. CONTENTS Foreword IISc at a Glance 8 1. The Institute 18 Court 5 Council 20 Finance Committee 21 Senate 21 Faculties 21 2. Staff (administration) 22 3. Divisions 25 3.1 Biological Sciences 26 3.2 Chemical Sciences 58 3.3 Electrical, Electronics, and Computer Sciences 86 3.4 Interdisciplinary Research 110 3.5 Mechanical Sciences 140 3.6 Physical and Mathematical Science 180 3.7 Centres under the Director 206 4. Undergraduate Programme 252 5. Awards/Distinctions 254 6. Students 266 6.1 Admissions & On Roll 267 6.2 SC/ST Students 267 6.3 Scholarships/Fellowships 267 6.4 Assistance Programme 267 6.5 Students Council 267 6.6 Hostels 267 6.7 Institute Medals 268 6.8 Awards & Distinctions 269 6.9 Placement 279 6.10 External Registration Program 279 6.11 Research Conferments 280 7. Events 300 7.1 Institute Lectures 310 7.2 Conferences/Seminars/Symposia/Workshops 302 8. -

October 2020
CSIR Foundation Day Celebration ISSN 0409-7467 CSIR News NEWSLETTER OF THE COUncIL OF SCIENTIFIC & INDUSTRIAL RESEARCH Volume 70 No. 10 website: http://www.csir.res.in October 2020 79th CSIR Foundation Day Special CSIR Celebrates 79th Foundation Day “It is indeed a privilege to be associated with CSIR in any capacity and you all have the great privilege of working for CSIR” — says Dr Harsh Vardhan Dr Harsh Vardhan, Union Minister of Science and Technology, Earth Sciences, Health and Family Welfare and Dr Shekhar C. Mande, DG, CSIR, during the lighting of the lamp THE Council of Scientific and Industrial Research small gathering at the SS Bhatnagar Sabhagar at (CSIR) celebrated its 79th Foundation Day on Anusandhan Bhawan, CSIR Headquarters in New 26 September 2020. In view of the COVID-19 Delhi maintaining social distancing. However, CSIR pandemic, the event was physically attended by a staff from all CSIR labs joined the occasion virtually. CSIR News October 2020 181 CSIR Foundation Day Celebration for CSIR.” Appreciating the efforts of CSIR, he said that he and Hon’ble Prime Minister have huge expectations and belief in the potential of CSIR and its scientists. Dr Harsh Vardhan said that whenever there has been a challenge before the country in any form, CSIR has always been able to convert it into an opportunity delivering innumerable benefits to the society. “The entire scientific community of India has been serving the cause of mitigation of COVID-19 in the best possible manner,” said the Hon’ble Minister. “Irrespective of the mandate and varied fields, all labs of CSIR contributed to the battle against the pandemic and Dr Harsh Vardhan addressing the gathering after six months of the active fight since the time of the lockdown, there are so many developments with us that could be called exclusive contributions of the CSIR family,” he added. -

Finn Lillelund Aachmann Eivind Aadland
PLOS ONE would like to thank all those who reviewed on behalf of the journal in 2015: Finn Lillelund Aachmann Yusuf Abba Eivind Aadland Nathlee Abbai Claus Aagaard Alexander Abbas Rasmus Aagaard Syed Abbas Philip Aagaard Ash Mohammad Abbas Eivind Aakhus Muhammad Abbas Ågot Aakra Ata Abbas Rob Aalberse Z. Abbas Lauri Aaltonen Aamir Abbas Mari Aaltonen James Abbas Eric Aamodt Faisal Abbas Håvard Aanes Saleem Abbasi Nikolaos Aantonakakis Ali Abbasi Ardalan Aarabi M. Kaleem Abbasi Jiska Aardoom Siddique Abbasi Julie Aarestrup S.A Abbasi Gloster Aaron Jennifer Abbass-Dick Erika Aaron Maggie Abbassi Shawn Aaron Jessica Abbate Philip Aaronson Mauro Abbate Scott Aaronson Giovanni Abbate-Daga Henk Aarts Souheila Abbeddou Jos Aarts Olivier Abbo Ellen Aasum Susan Abbondanzo Mohd Nadhir Ab Wahab Derek Abbott Jose Abad David H. Abbott Jorge Abad Jessica Abbott Francisca Abad William Abbott Eduardo Abade Sabra Abbott Fernando Abad-Franch Daniel Abbott Fitsum Abadi Andrew Abbott Javier Abadia Peter Abbott Valerie Abadie Gavin Abbott Tatjana Abaffy Giovanni Abbruzzese Grace Abakpa Sophie Abby Xesus Abalo Ekram Abd El Wahab Inmaculada Aban Ahmed Abd El Wahed Daniel Abankwa Aini Ismafairus Abd Hamid Jenny Abanto M Abdalla Federico Abascal Walid Abdallah Aniekan Abasiattai F Abdallah Zaid Abassi Mohamed Abdel Hakeem Solomon Abay Bahaa-Eldin Abdel Rahim Mohamed Abdelbary Keiko Abe Mohamed Abdel-Daim Takeru Abe Hesham Abdeldayem Nobuhito Abe Sonia Abdelhak Toshiaki Abe Asmaa Abdelhamid Hiroshi Abe Maha Abdelhaq Kensaku Abe Nasser Abdel-Latif Keietsu Abe Ahmad -

Awardees of National Bioscience Award for Career Development
AWARDEES OF NATIONAL BIOSCIENCE AWARD FOR CAREER DEVELOPMENT Awardees for the year 2016 1. Dr. Mukesh Jain, Associate Professor, School of Computational and Integrative Sciences, Jawaharlal Nehru University, New Delhi-110067 2. Dr. Samir K. Maji, Associate Professor, Indian Institute of Technology, Powai, Mumbai- 400076 3. Dr. Anindita Ukil, Assistant Professor, Calcutta University, Kolkata 4. Dr. Arnab Mukhopadhyay, Staff Scientist V, National Institute of Immunology, Aruna Asaf Ali Marg, New Delhi- 110067 5. Dr. Rohit Srivastava, Professor, Indian Institute of Technology, Bombay, Mumbai- 400076 6. Dr. Pinaki Talukdar, Associate Professor, Indian Institute of Science Education and Research, Dr. Homi Bhabha Road, Pashan, Pune- 7. Dr. Rajnish Kumar Chaturvedi, Senior Scientist, CSIR- Indian Institute of Toxicology Research, Lucknow-226001 8. Dr. Jackson James, Scientist E-II, Neuro Stem Cell Biology Lab, Neurobiology Division, Rajiv Gandhi Centre for Biotechnology, Thiruvananthapuram, Kerala- 695014 Awardees for the year 2015 1. Dr. Sanjeev Das, Staff Scientist-V, National Institute of Immunology, New Delhi 2. Dr. Ganesh Nagaraju, Assistant Professor, Department of Biotechnology, Indian Institute of Science, Bangalore- 5600012. 3. Dr. Suvendra Nath Bhattacharya, Principal Scientist, CSIR- Indian Institute of Chemical Biology, Kolkata- 700032 4. Dr. Thulasiram H V, Principal Scientist, CSIR-National Chemical Laboratory, Pune- 411008. 5. Dr. Pawan Gupta, Principal Scientist, Institute of microbial Technology, Chandigarh- 160036. 6. Dr. Souvik Maiti, Principal Scientist, CSIR-Institute of Genomics and Integrative Biology, Delhi- 110025. 7. Dr. Pravindra Kumar, Associate Professor, Department of Biotechnology, IIT, Roorkee- 247667. 8. Dr. Anurag Agrawal, Principal Scientist, CSIR-Institute of Genomics and Integrative Biology, Delhi- 110025 9. Dr. Gridhar Kumar Pandey, Professor, Department of Plant Molecular Biology, University of Delhi South Campus, New Delhi- 110067 10. -

Annual Report 2010-11
Contents Sl. No. Contents Page No. 1. Director’s Report 01 2. Organization 19 IIT Council The Board of Governors The Finance Committee The Building & Works Committee The Senate 3. The Faculty 49 4. Academic Programmes 66 5. Research & Development 82 6. Alumni Association Activities 104 7. Central Facilities 111 P K Kelkar Library Computer Centre Centre for Development of Technical Education Centre for Creative Writing and Publication Staff Training Unit SC/ST and OBC Cell Rajbhasha Prakoshtha Media Technology Centre 8. Finance 135 9. Endowment Report 137 10. Facilities to Students 139 11. Students’ Placement 153 12. Services/Amenities 156 Institute Works Department Stores & Purchase Section Estate Office Campus School Health Centre Visitors’ Hostel 13. Publication and Outreach Activities 167 Books & Book–chapters Published Journals Papers Research Papers Published In Conference Proceedings Papers presented in seminars/conference/workshops/symposia Invited talks delivered Other activities Annual Report 2010-2011 Director’s Report Honorable Chairman, Board of Governors of the Indian Institute of Technology Kanpur, Professor M. Anandakrishnan, Distinguished Chief Guest, Prof. P. Balaram, Members of the Board of Governors, Members of the Academic Senate, all graduating students and their family members, all members of faculty, staff and students, invited dignitaries, guests, and members of the media: I heartily welcome you all on this occasion of the forty-third convocation of the Indian Institute of Technology Kanpur. We are particularly happy to welcome Prof. P. Balaram, Director, Indian Institute of Science, Bangalore, amongst us for today’s forty- third convocation. The academic year closing in May 2011 has been momentous, and I consider it a privilege to review our activities pertaining to this period. -

The Year Book 2017
THE YEAR BOOK 2017 INDIAN ACADEMY OF SCIENCES Bengaluru Postal Address: Indian Academy of Sciences Post Box No. 8005 C.V. Raman Avenue Sadashivanagar Post, Raman Research Institute Campus Bengaluru 560 080 India Telephone : +91-80-2266 1200, +91-80-2266 1203 Fax : +91-80-2361 6094 Email : [email protected], [email protected] Website : www.ias.ac.in © 2017 Indian Academy of Sciences Editorial & Production Team: Nalini, B.R. Thirumalai, N. Vanitha, M. Venugopal, M.S. Published by: Executive Secretary, Indian Academy of Sciences Text formatted by WINTECS Typesetters, Bengaluru (Ph. +91-80-2332 7311) Printed by Tholasi Prints India Pvt. Ltd., Bengaluru (Ph: +91-80-4047 0000) CONTENTS Page Section A: Indian Academy of Sciences Memorandum of Association ............................................... 2 Role of the Academy........................................................... 4 Statutes ............................................................................. 7 Council for the period 2016–2018 ........................................ 18 Office Bearers .................................................................... 19 Former Presidents .............................................................. 20 Activities – a profile............................................................. 21 Section B: Professorships Raman Chair ...................................................................... 26 Jubilee Chair ...................................................................... 29 Section C: Fellowship and Honorary Fellowship Fellows -

National Bioscience Awards for Career Development
AWARDEES OF NATIONAL BIOSCIENCE AWARDS FOR CAREER DEVELOPMENT Awardees for the year 2012 1. Dr. Kaustuv Sanyal, Associate Professor, Molecular Mycology Laboratory, Molecular Biology & Genetics Unit, Jawaharlal Nehru Centre for Advance Scientific Research, Jakkur P.O. Bangalore 560064 2. Dr Naval Kishore Vikram, Associate Professor, Department of Medicine, All India Institute of Medical Sciences (AIIMS), Ansari Nagar, New Delhi- 110029 3. Dr. Aditya Bhushan Pant, Senior Scientist & In-charge, In Vitro Toxicology Laboratory, Indian Institute of Toxicology Research, PO Box: 80, MG Marg, Lucknow 226001 (UP) India 4. Dr. Subrata Adak, Senior Scientist, Indian Institute of Chemical Biology; 4, Raja S.C. Mullick Road, Kolkata-700032 5. Dr. Durai Sundar, Assistant Professor, Dept of Biochemical Engineering & Biotechnology, Indian Institute of Technology (IIT) Delhi, Hauz Khas, New Delhi – 110016 6. Dr S Venkata Mohan, Senior Scientist, Bioengineering and Environmental Centre (BEEC) CSIR-Indian Institute of Chemical Technology, Hyderabad-500 607 7. Dr. Munia Ganguli, Scientist E-I, CSIR-Institute of Genomics & Integrative Biology, Mall Road,New Delhi 110 007 8. Dr. Asad U Khan, Associate Professor & Coordinator/Head of Biotechnology Department, A.M.U, Interdisciplinary Biotechnology Unit, A.M.U., Aligarh 202002 9. Dr. Sathees C. Raghavan, Assistant Professor, Department of Biochemistry, Indian Institute of Science, Bangalore 560 012 10. Dr. Vidita A. Vaidya, Associate Professor, Department of Biological Sciences, Tata Institute of Fundamental Research, 1, Homi Bhabha Road, Colaba, Mumbai - 400005 Awardees for the year 2011 1. Dr. M. M. Parida, Scientist-F, Joint Director, Division of Virology Defence R & D Establishment, DRDE, DRDO, Ministry of Defence, Jhansi Road, Gwalior- 474002 2. -
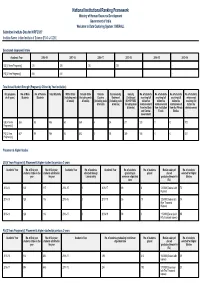
Data Submitted for NIRF Ranking 2020 – Iisc
National Institutional Ranking Framework Ministry of Human Resource Development Government of India Welcome to Data Capturing System: OVERALL Submitted Institute Data for NIRF'2020' Institute Name: Indian Institute of Science [IR-O-U-0220] Sanctioned (Approved) Intake Academic Year 2018-19 2017-18 2016-17 2015-16 2014-15 2013-14 UG [4 Years Program(s)] 120 120 120 120 - - PG [2 Year Program(s)] 456 441 - - - - Total Actual Student Strength (Program(s) Offered by Your Institution) (All programs No. of Male No. of Female Total Students Within State Outside State Outside Economically Socially No. of students No. of students No. of students No. of students of all years) Students Students (Including male (Including male Country Backward Challenged receiving full receiving full receiving full who are not & female) & female) (Including male (Including male (SC+ST+OBC tuition fee tuition fee tuition fee receiving full & female) & female) Including male reimbursement reimbursement reimbursement tuition fee & female) from the State from Institution from the Private reimbursement and Central Funds Bodies Government UG [4 Years 368 68 436 63 369 4 24 211 133 0 0 102 Program(s)] PG [2 Year 607 99 706 54 652 0 38 349 146 0 0 241 Program(s)] Placement & Higher Studies UG [4 Years Program(s)]: Placement & higher studies for previous 3 years Academic Year No. of first year No. of first year Academic Year No. of students Academic Year No. of students No. of students Median salary of No. of students students intake in the students admitted in admitted through graduating in placed placed selected for Higher year the year Lateral entry minimum stipulated graduates(Amount in Studies time Rs.) 2013-14 120 117 2014-15 0 2016-17 89 6 1200000(Twelve Lakh 74 Rupees) 2014-15 120 116 2015-16 0 2017-18 86 10 1250000(Twelve lakh 74 fiftye Thousand Ruppes) 2015-16 120 116 2016-17 0 2018-19 98 3 1150000(Eleven Lakh 95 Fifty thousand rupees) PG [2 Years Program(s)]: Placement & higher studies for previous 3 years Academic Year No. -

Annual Report 2011-12
Contents Sl. No. Contents Page No. 1. Director’s Report 1 2. Organization 19 IIT Council The Board of Governors The Finance Committee The Building & Works Committee The Senate 3. The Faculty 44 4. Academic Programmes 59 5. Research & Development 70 6. Alumni Association Activities 85 7. Central Facilities 90 P K Kelkar Library Computer Centre Centre for Development of Technical Education Centre for Creative Writing and Publication Staff Training Unit SC/ST and OBC Cell Rajbhasha Prakoshtha Media Technology Centre 8. Finance 112 9. Endowment Report 114 10. Facilities to Students 117 11. Students’ Placement 130 12. Services/Amenities 134 Institute Works Department Stores & Purchase Section Estate Office Campus School Health Centre Visitors’ Hostel 13. Publication and Outreach Activities 146 Books & Book–chapters Published Journals Papers Research Papers Published In Conference Proceedings Papers presented in seminars/conference/ workshops/ symposia Invited talks delivered Other activities Annual Report 2011-12 Director’s Report Honourable Chairman, Board of Governors of the Indian Institute of Technology Kanpur, Professor M. Anandakrishnan, Distinguished Chief Guest, Dr. E. Sreedharan, Members of the Board of Governors, Members of the Academic Senate, all graduating students and their family members, members of faculty, staff and students, invited dignitaries, guests, and members of the media: I heartily welcome you all on this occasion of the forty-fourth convocation of the Indian Institute of Technology Kanpur. We are particularly happy to welcome Dr. E. Sreedharan, Padmavibhushan, former Managing Director of Delhi Metro, amongst us for today’s forty - fourth convocation. The academic year closing in May 2012 has been momentous, and I consider it a privilege to review our activities pertaining to this period.