15-853:Algorithms in the Real World
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Planar Graph Theory We Say That a Graph Is Planar If It Can Be Drawn in the Plane Without Edges Crossing
Planar Graph Theory We say that a graph is planar if it can be drawn in the plane without edges crossing. We use the term plane graph to refer to a planar depiction of a planar graph. e.g. K4 is a planar graph Q1: The following is also planar. Find a plane graph version of the graph. A B F E D C A Method that sometimes works for drawing the plane graph for a planar graph: 1. Find the largest cycle in the graph. 2. The remaining edges must be drawn inside/outside the cycle so that they do not cross each other. Q2: Using the method above, find a plane graph version of the graph below. A B C D E F G H non e.g. K3,3: K5 Here are three (plane graph) depictions of the same planar graph: J N M J K J N I M K K I N M I O O L O L L A face of a plane graph is a region enclosed by the edges of the graph. There is also an unbounded face, which is the outside of the graph. Q3: For each of the plane graphs we have drawn, find: V = # of vertices of the graph E = # of edges of the graph F = # of faces of the graph Q4: Do you have a conjecture for an equation relating V, E and F for any plane graph G? Q5: Can you name the 5 Platonic Solids (i.e. regular polyhedra)? (This is a geometry question.) Q6: Find the # of vertices, # of edges and # of faces for each Platonic Solid. -

Bandwidth, Expansion, Treewidth, Separators and Universality for Bounded-Degree Graphs$
View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by Elsevier - Publisher Connector European Journal of Combinatorics 31 (2010) 1217–1227 Contents lists available at ScienceDirect European Journal of Combinatorics journal homepage: www.elsevier.com/locate/ejc Bandwidth, expansion, treewidth, separators and universality for bounded-degree graphsI Julia Böttcher a, Klaas P. Pruessmann b, Anusch Taraz a, Andreas Würfl a a Zentrum Mathematik, Technische Universität München, Boltzmannstraße 3, D-85747 Garching bei München, Germany b Institute for Biomedical Engineering, University and ETH Zurich, Gloriastr. 35, 8092, Zürich, Switzerland article info a b s t r a c t Article history: We establish relations between the bandwidth and the treewidth Received 3 March 2009 of bounded degree graphs G, and relate these parameters to the size Accepted 13 October 2009 of a separator of G as well as the size of an expanding subgraph of Available online 24 October 2009 G. Our results imply that if one of these parameters is sublinear in the number of vertices of G then so are all the others. This implies for example that graphs of fixed genus have sublinear bandwidth or, more generally, a corresponding result for graphs with any fixed forbidden minor. As a consequence we establish a simple criterion for universality for such classes of graphs and show for example that for each γ > 0 every n-vertex graph with minimum degree 3 C . 4 γ /n contains a copy of every bounded-degree planar graph on n vertices if n is sufficiently large. ' 2009 Elsevier Ltd. -

Characterizations of Restricted Pairs of Planar Graphs Allowing Simultaneous Embedding with Fixed Edges
Characterizations of Restricted Pairs of Planar Graphs Allowing Simultaneous Embedding with Fixed Edges J. Joseph Fowler1, Michael J¨unger2, Stephen Kobourov1, and Michael Schulz2 1 University of Arizona, USA {jfowler,kobourov}@cs.arizona.edu ⋆ 2 University of Cologne, Germany {mjuenger,schulz}@informatik.uni-koeln.de ⋆⋆ Abstract. A set of planar graphs share a simultaneous embedding if they can be drawn on the same vertex set V in the Euclidean plane without crossings between edges of the same graph. Fixed edges are common edges between graphs that share the same simple curve in the simultaneous drawing. Determining in polynomial time which pairs of graphs share a simultaneous embedding with fixed edges (SEFE) has been open. We give a necessary and sufficient condition for when a pair of graphs whose union is homeomorphic to K5 or K3,3 can have an SEFE. This allows us to determine which (outer)planar graphs always an SEFE with any other (outer)planar graphs. In both cases, we provide efficient al- gorithms to compute the simultaneous drawings. Finally, we provide an linear-time decision algorithm for deciding whether a pair of biconnected outerplanar graphs has an SEFE. 1 Introduction In many practical applications including the visualization of large graphs and very-large-scale integration (VLSI) of circuits on the same chip, edge crossings are undesirable. A single vertex set can be used with multiple edge sets that each correspond to different edge colors or circuit layers. While the pairwise union of all edge sets may be nonplanar, a planar drawing of each layer may be possible, as crossings between edges of distinct edge sets are permitted. -

Separator Theorems and Turán-Type Results for Planar Intersection Graphs
SEPARATOR THEOREMS AND TURAN-TYPE¶ RESULTS FOR PLANAR INTERSECTION GRAPHS JACOB FOX AND JANOS PACH Abstract. We establish several geometric extensions of the Lipton-Tarjan separator theorem for planar graphs. For instance, we show that any collection C of Jordan curves in the plane with a total of m p 2 crossings has a partition into three parts C = S [ C1 [ C2 such that jSj = O( m); maxfjC1j; jC2jg · 3 jCj; and no element of C1 has a point in common with any element of C2. These results are used to obtain various properties of intersection patterns of geometric objects in the plane. In particular, we prove that if a graph G can be obtained as the intersection graph of n convex sets in the plane and it contains no complete bipartite graph Kt;t as a subgraph, then the number of edges of G cannot exceed ctn, for a suitable constant ct. 1. Introduction Given a collection C = fγ1; : : : ; γng of compact simply connected sets in the plane, their intersection graph G = G(C) is a graph on the vertex set C, where γi and γj (i 6= j) are connected by an edge if and only if γi \ γj 6= ;. For any graph H, a graph G is called H-free if it does not have a subgraph isomorphic to H. Pach and Sharir [13] started investigating the maximum number of edges an H-free intersection graph G(C) on n vertices can have. If H is not bipartite, then the assumption that G is an intersection graph of compact convex sets in the plane does not signi¯cantly e®ect the answer. -

Sphere-Cut Decompositions and Dominating Sets in Planar Graphs
Sphere-cut Decompositions and Dominating Sets in Planar Graphs Michalis Samaris R.N. 201314 Scientific committee: Dimitrios M. Thilikos, Professor, Dep. of Mathematics, National and Kapodistrian University of Athens. Supervisor: Stavros G. Kolliopoulos, Dimitrios M. Thilikos, Associate Professor, Professor, Dep. of Informatics and Dep. of Mathematics, National and Telecommunications, National and Kapodistrian University of Athens. Kapodistrian University of Athens. white Lefteris M. Kirousis, Professor, Dep. of Mathematics, National and Kapodistrian University of Athens. Aposunjèseic sfairik¸n tom¸n kai σύνοla kuriarqÐac se epÐpeda γραφήματa Miχάλης Σάμαρης A.M. 201314 Τριμελής Epiτροπή: Δημήτρioc M. Jhlυκός, Epiblèpwn: Kajhγητής, Tm. Majhmatik¸n, E.K.P.A. Δημήτρioc M. Jhlυκός, Staύρoc G. Kolliόποuloc, Kajhγητής tou Τμήμatoc Anaπληρωτής Kajhγητής, Tm. Plhroforiκής Majhmatik¸n tou PanepisthmÐou kai Thl/ni¸n, E.K.P.A. Ajhn¸n Leutèrhc M. Kuroύσης, white Kajhγητής, Tm. Majhmatik¸n, E.K.P.A. PerÐlhyh 'Ena σημαντικό apotèlesma sth JewrÐa Γραφημάτwn apoteleÐ h apόdeixh thc eikasÐac tou Wagner από touc Neil Robertson kai Paul D. Seymour. sth σειρά ergasi¸n ‘Ελλάσσοna Γραφήματα’ apo to 1983 e¸c to 2011. H eikasÐa αυτή lèei όti sthn κλάση twn γραφημάtwn den υπάρχει άπειρη antialusÐda ¸c proc th sqèsh twn ελλασόnwn γραφημάτwn. H JewrÐa pou αναπτύχθηκε gia thn απόδειξη αυτής thc eikasÐac eÐqe kai èqei ακόμα σημαντικό antÐktupo tόσο sthn δομική όσο kai sthn algoriθμική JewrÐa Γραφημάτwn, άλλα kai se άλλα pedÐa όπως h Παραμετρική Poλυπλοκόthta. Sta πλάιsia thc απόδειξης oi suggrafeÐc eiσήγαγαν kai nèec paramètrouc πλά- touc. Se autèc ήτan h κλαδοαποσύνθεση kai to κλαδοπλάτoc ενός γραφήματoc. H παράμετρος αυτή χρησιμοποιήθηκε idiaÐtera sto σχεδιασμό algorÐjmwn kai sthn χρήση thc τεχνικής ‘διαίρει kai basÐleue’. -

Treewidth-Erickson.Pdf
Computational Topology (Jeff Erickson) Treewidth Or il y avait des graines terribles sur la planète du petit prince . c’étaient les graines de baobabs. Le sol de la planète en était infesté. Or un baobab, si l’on s’y prend trop tard, on ne peut jamais plus s’en débarrasser. Il encombre toute la planète. Il la perfore de ses racines. Et si la planète est trop petite, et si les baobabs sont trop nombreux, ils la font éclater. [Now there were some terrible seeds on the planet that was the home of the little prince; and these were the seeds of the baobab. The soil of that planet was infested with them. A baobab is something you will never, never be able to get rid of if you attend to it too late. It spreads over the entire planet. It bores clear through it with its roots. And if the planet is too small, and the baobabs are too many, they split it in pieces.] — Antoine de Saint-Exupéry (translated by Katherine Woods) Le Petit Prince [The Little Prince] (1943) 11 Treewidth In this lecture, I will introduce a graph parameter called treewidth, that generalizes the property of having small separators. Intuitively, a graph has small treewidth if it can be recursively decomposed into small subgraphs that have small overlap, or even more intuitively, if the graph resembles a ‘fat tree’. Many problems that are NP-hard for general graphs can be solved in polynomial time for graphs with small treewidth. Graphs embedded on surfaces of small genus do not necessarily have small treewidth, but they can be covered by a small number of subgraphs, each with small treewidth. -
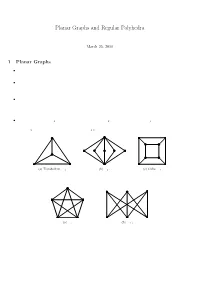
Planar Graphs and Regular Polyhedra
Planar Graphs and Regular Polyhedra March 25, 2010 1 Planar Graphs ² A graph G is said to be embeddable in a plane, or planar, if it can be drawn in the plane in such a way that no two edges cross each other. Such a drawing is called a planar embedding of the graph. ² Let G be a planar graph and be embedded in a plane. The plane is divided by G into disjoint regions, also called faces of G. We denote by v(G), e(G), and f(G) the number of vertices, edges, and faces of G respectively. ² Strictly speaking, the number f(G) may depend on the ways of drawing G on the plane. Nevertheless, we shall see that f(G) is actually independent of the ways of drawing G on any plane. The relation between f(G) and the number of vertices and the number of edges of G are related by the well-known Euler Formula in the following theorem. ² The complete graph K4, the bipartite complete graph K2;n, and the cube graph Q3 are planar. They can be drawn on a plane without crossing edges; see Figure 5. However, by try-and-error, it seems that the complete graph K5 and the complete bipartite graph K3;3 are not planar. (a) Tetrahedron, K4 (b) K2;5 (c) Cube, Q3 Figure 1: Planar graphs (a) K5 (b) K3;3 Figure 2: Nonplanar graphs Theorem 1.1. (Euler Formula) Let G be a connected planar graph with v vertices, e edges, and f faces. Then v ¡ e + f = 2: (1) 1 (a) Octahedron (b) Dodecahedron (c) Icosahedron Figure 3: Regular polyhedra Proof. -

1 Plane and Planar Graphs Definition 1 a Graph G(V,E) Is Called Plane If
1 Plane and Planar Graphs Definition 1 A graph G(V,E) is called plane if • V is a set of points in the plane; • E is a set of curves in the plane such that 1. every curve contains at most two vertices and these vertices are the ends of the curve; 2. the intersection of every two curves is either empty, or one, or two vertices of the graph. Definition 2 A graph is called planar, if it is isomorphic to a plane graph. The plane graph which is isomorphic to a given planar graph G is said to be embedded in the plane. A plane graph isomorphic to G is called its drawing. 1 9 2 4 2 1 9 8 3 3 6 8 7 4 5 6 5 7 G is a planar graph H is a plane graph isomorphic to G 1 The adjacency list of graph F . Is it planar? 1 4 56 8 911 2 9 7 6 103 3 7 11 8 2 4 1 5 9 12 5 1 12 4 6 1 2 8 10 12 7 2 3 9 11 8 1 11 36 10 9 7 4 12 12 10 2 6 8 11 1387 12 9546 What happens if we add edge (1,12)? Or edge (7,4)? 2 Definition 3 A set U in a plane is called open, if for every x ∈ U, all points within some distance r from x belong to U. A region is an open set U which contains polygonal u,v-curve for every two points u,v ∈ U. -

Ma/CS 6B Class 8: Planar and Plane Graphs
1/26/2017 Ma/CS 6b Class 8: Planar and Plane Graphs By Adam Sheffer The Utilities Problem Problem. There are three houses on a plane. Each needs to be connected to the gas, water, and electricity companies. ◦ Is there a way to make all nine connections without any of the lines crossing each other? ◦ Using a third dimension or sending connections through a company or house is not allowed. 1 1/26/2017 Rephrasing as a Graph How can we rephrase the utilities problem as a graph problem? ◦ Can we draw 퐾3,3 without intersecting edges. Closed Curves A simple closed curve (or a Jordan curve) is a curve that does not cross itself and separates the plane into two regions: the “inside” and the “outside”. 2 1/26/2017 Drawing 퐾3,3 with no Crossings We try to draw 퐾3,3 with no crossings ◦ 퐾3,3 contains a cycle of length six, and it must be drawn as a simple closed curve 퐶. ◦ Each of the remaining three edges is either fully on the inside or fully on the outside of 퐶. 퐾3,3 퐶 No 퐾3,3 Drawing Exists We can only add one red-blue edge inside of 퐶 without crossings. Similarly, we can only add one red-blue edge outside of 퐶 without crossings. Since we need to add three edges, it is impossible to draw 퐾3,3 with no crossings. 퐶 3 1/26/2017 Drawing 퐾4 with no Crossings Can we draw 퐾4 with no crossings? ◦ Yes! Drawing 퐾5 with no Crossings Can we draw 퐾5 with no crossings? ◦ 퐾5 contains a cycle of length five, and it must be drawn as a simple closed curve 퐶. -

What Is a Polyhedron?
3. POLYHEDRA, GRAPHS AND SURFACES 3.1. From Polyhedra to Graphs What is a Polyhedron? Now that we’ve covered lots of geometry in two dimensions, let’s make things just a little more difficult. We’re going to consider geometric objects in three dimensions which can be made from two-dimensional pieces. For example, you can take six squares all the same size and glue them together to produce the shape which we call a cube. More generally, if you take a bunch of polygons and glue them together so that no side gets left unglued, then the resulting object is usually called a polyhedron.1 The corners of the polygons are called vertices, the sides of the polygons are called edges and the polygons themselves are called faces. So, for example, the cube has 8 vertices, 12 edges and 6 faces. Different people seem to define polyhedra in very slightly different ways. For our purposes, we will need to add one little extra condition — that the volume bound by a polyhedron “has no holes”. For example, consider the shape obtained by drilling a square hole straight through the centre of a cube. Even though the surface of such a shape can be constructed by gluing together polygons, we don’t consider this shape to be a polyhedron, because of the hole. We say that a polyhedron is convex if, for each plane which lies along a face, the polyhedron lies on one side of that plane. So, for example, the cube is a convex polyhedron while the more complicated spec- imen of a polyhedron pictured on the right is certainly not convex. -

Planarity and Duality of Finite and Infinite Graphs
JOURNAL OF COMBINATORIAL THEORY, Series B 29, 244-271 (1980) Planarity and Duality of Finite and Infinite Graphs CARSTEN THOMASSEN Matematisk Institut, Universitets Parken, 8000 Aarhus C, Denmark Communicated by the Editors Received September 17, 1979 We present a short proof of the following theorems simultaneously: Kuratowski’s theorem, Fary’s theorem, and the theorem of Tutte that every 3-connected planar graph has a convex representation. We stress the importance of Kuratowski’s theorem by showing how it implies a result of Tutte on planar representations with prescribed vertices on the same facial cycle as well as the planarity criteria of Whit- ney, MacLane, Tutte, and Fournier (in the case of Whitney’s theorem and MacLane’s theorem this has already been done by Tutte). In connection with Tutte’s planarity criterion in terms of non-separating cycles we give a short proof of the result of Tutte that the induced non-separating cycles in a 3-connected graph generate the cycle space. We consider each of the above-mentioned planarity criteria for infinite graphs. Specifically, we prove that Tutte’s condition in terms of overlap graphs is equivalent to Kuratowski’s condition, we characterize completely the infinite graphs satisfying MacLane’s condition and we prove that the 3- connected locally finite ones have convex representations. We investigate when an infinite graph has a dual graph and we settle this problem completely in the locally finite case. We show by examples that Tutte’s criterion involving non-separating cy- cles has no immediate extension to infinite graphs, but we present some analogues of that criterion for special classes of infinite graphs. -

Linearity of Grid Minors in Treewidth with Applications Through Bidimensionality∗
Linearity of Grid Minors in Treewidth with Applications through Bidimensionality∗ Erik D. Demaine† MohammadTaghi Hajiaghayi† Abstract We prove that any H-minor-free graph, for a fixed graph H, of treewidth w has an Ω(w) × Ω(w) grid graph as a minor. Thus grid minors suffice to certify that H-minor-free graphs have large treewidth, up to constant factors. This strong relationship was previously known for the special cases of planar graphs and bounded-genus graphs, and is known not to hold for general graphs. The approach of this paper can be viewed more generally as a framework for extending combinatorial results on planar graphs to hold on H-minor-free graphs for any fixed H. Our result has many combinatorial consequences on bidimensionality theory, parameter-treewidth bounds, separator theorems, and bounded local treewidth; each of these combinatorial results has several algorithmic consequences including subexponential fixed-parameter algorithms and approximation algorithms. 1 Introduction The r × r grid graph1 is the canonical planar graph of treewidth Θ(r). In particular, an important result of Robertson, Seymour, and Thomas [38] is that every planar graph of treewidth w has an Ω(w) × Ω(w) grid graph as a minor. Thus every planar graph of large treewidth has a grid minor certifying that its treewidth is almost as large (up to constant factors). In their Graph Minor Theory, Robertson and Seymour [36] have generalized this result in some sense to any graph excluding a fixed minor: for every graph H and integer r > 0, there is an integer w > 0 such that every H-minor-free graph with treewidth at least w has an r × r grid graph as a minor.